
Intuitionistic type theory
Encyclopedia
Intuitionistic type theory, or constructive type theory, or Martin-Löf type theory or just Type Theory is a logical system and a set theory
based on the principles of mathematical constructivism. Intuitionistic type theory was introduced by Per Martin-Löf
, a Swedish
mathematician
and philosopher, in 1972. Martin-Löf has modified his proposal a few times; his 1971 impredicative
formulation was inconsistent as demonstrated by Girard's paradox. Later formulations were predicative
. He proposed both intensional
and extensional
variants of the theory.
Intuitionistic type theory is based on a certain analogy or isomorphism between proposition
s and types
: a proposition is identified with the type of its proofs. This identification is usually called the Curry–Howard isomorphism, which was originally formulated for intuitionistic logic
and simply typed lambda calculus
. Type Theory extends this identification to predicate logic
by introducing dependent types, that is types which contain values.
Type Theory internalizes the interpretation of intuitionistic logic
proposed by Brouwer
, Heyting
and Kolmogorov
, the so called BHK interpretation
. The types of Type Theory play a similar role to sets in set theory
but functions definable in Type Theory are always computable.
is a way of constructing types, possibly using already given types.
The basic connectives of Type Theory are:
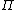 -types, also called dependent product types, are analogous to the indexed products
-types, also called dependent product types, are analogous to the indexed products
of sets. As such, they generalize the normal function space
to model functions whose result type may vary on their input. E.g. writing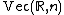 for
for  -tuples of real numbers,
-tuples of real numbers, 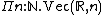 stands for the type of functions which given a natural number
stands for the type of functions which given a natural number
returns a tuple of real numbers of this size. The usual function space arises as a special case when the range type does not actually depend on the input, e.g.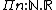 is the type of functions from natural numbers to the real numbers, which is also written as
is the type of functions from natural numbers to the real numbers, which is also written as 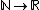 . Using the Curry–Howard isomorphism
. Using the Curry–Howard isomorphism 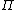 -types also serve to model implication
-types also serve to model implication
and universal quantification
: e.g. a term inhabiting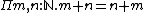 is a function which assigns to any pair of natural numbers a proof that addition is commutative for that pair and hence can be considered as a proof that addition is commutative for all natural numbers.
is a function which assigns to any pair of natural numbers a proof that addition is commutative for that pair and hence can be considered as a proof that addition is commutative for all natural numbers.
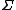 -types, also called dependent sum types, are analogous to the indexed disjoint union
-types, also called dependent sum types, are analogous to the indexed disjoint union
s of sets. As such, they generalize the usual Cartesian product
to model pairs where the type of the 2nd component depends on the first. E.g. the type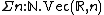 stands for the type of pairs of a natural number
stands for the type of pairs of a natural number
and a tuple
of real numbers of that size, i.e. this type can be used to model sequences of arbitrary length (usually called lists). The conventional Cartesian product
type arises as a special case when the type of the 2nd component doesn't actually depend on the first, e.g.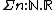 is the type of pairs of a natural number
is the type of pairs of a natural number
and a real number
, which is also written as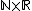 . Again, using the Curry–Howard isomorphism,
. Again, using the Curry–Howard isomorphism, 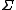 -types also serve to model conjunction
-types also serve to model conjunction
and existential quantification
.
) and 2 (the type of Booleans or classical truth values). Invoking the Curry–Howard isomorphism again, ⊥ stands for False and ⊤ for True.
Using finite types we can define negation
as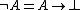 .
.
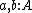 then
then 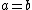 is the type of equality proofs that
is the type of equality proofs that  is equal to
is equal to 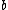 . There is only one (canonical) inhabitant of
. There is only one (canonical) inhabitant of  and this is the proof of reflexivity
and this is the proof of reflexivity 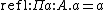 .
.
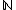 which is generated by
which is generated by 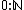 and
and 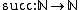 . An important application of the propositions as types principle is the identification of (dependent) primitive recursion and induction
. An important application of the propositions as types principle is the identification of (dependent) primitive recursion and induction
by one elimination constant: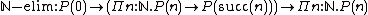 for any given type
for any given type 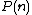 indexed by
indexed by 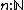 . In general inductive types can be defined in terms of W-types, the type of well-founded trees.
. In general inductive types can be defined in terms of W-types, the type of well-founded trees.
An important class of inductive types are inductive families like the type of vectors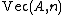 mentioned above, which is inductively generated by the constructors
mentioned above, which is inductively generated by the constructors 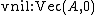 and
and 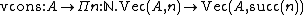 . Applying the Curry–Howard isomorphism once more, inductive families correspond to inductively defined relations.
. Applying the Curry–Howard isomorphism once more, inductive families correspond to inductively defined relations.
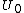 , the universe of all small types, which contains names for all the types introduced so far. To every name
, the universe of all small types, which contains names for all the types introduced so far. To every name 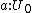 we associate a type
we associate a type 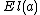 , its extension or meaning. It is standard to assume a predicative hierarchy of universes:
, its extension or meaning. It is standard to assume a predicative hierarchy of universes: 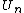 for every natural number
for every natural number 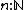 , where the universe
, where the universe 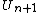 contains a code for the previous universe, i.e. we have
contains a code for the previous universe, i.e. we have 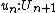 with
with 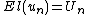 . This hierarchy is often assumed to be cumulative, that is the codes from
. This hierarchy is often assumed to be cumulative, that is the codes from 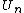 are embedded in
are embedded in 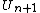 .
.
Stronger universe principles have been investigated, i.e. super universes and the Mahlo universe. In 1992 Huet and Coquand introduced the calculus of constructions
, a type theory with an impredicative universe, thus combining Type Theory with Girard
's System F
. This extension is not universally accepted by Intuitionists since it allows impredicative, i.e. circular, constructions, which are often identified with classical reasoning.
, using the judgements:
Of special importance is the conversion rule, which says that given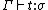 and
and 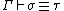 then
then 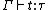 .
.
, R.A.G. Seely introduced the notion of a locally cartesian closed category (LCCC) as the basic model of Type Theory. This has been refined by Hofmann and Dybjer to Categories with Families or Categories with Attributes based on earlier work by Cartmell.
A category with families is a category C of contexts (in which the objects are contexts, and
the context morphisms are substitutions), together with a functor T : Cop → Fam(Set).
Fam(Set) is the category of families of Sets, in which objects are pairs (A,B) of an "index set" A and a function B: X → A, and morphisms are pairs of functions f : A → A' and g : X → X' , such that B' ° g = f ° B - in other words, f maps Ba to B'g(a).
The functor T assigns to a context G a set Ty(G) of types, and for each A : Ty(G), a set Tm(G,A) of terms.
The axioms for a functor require that these play harmoniously with substitution. Substitution is usually
written in the form Af or af, where A is a type in Ty(G) and a is a term in Tm(G,A), and f is a substitution
from D to G. Here Af : Ty(D) and af : Tm(D,Af).
The category C must contain a terminal object (the empty context), and a final object for a form
of product called comprehension, or context extension, in which the right element is a type in the context of the left element.
If G is a context, and A : Ty(G), then there should be an object (G,A) final among
contexts D with mappings p : D → G, q : Tm(D,Ap).
A logical framework, such as Martin-Löf's takes the form of
closure conditions on the context dependent sets of types and terms: that there should be a type called
Set, and for each set a type, that the types should be closed under forms of dependent sum and
product, and so forth.
A theory such as that of predicative set theory expresses closure conditions on the types of sets and
their elements: that they should be closed under operations that reflect dependent sum and product,
and under various forms of inductive definition.
vs intensional
Type Theory. In extensional Type Theory definitional (i.e. computational) equality is not distinguished from propositional equality, which requires proof. As a consequence type checking becomes undecidable
in extensional type theory. This is because relying on computational equality means that the equality depends on computations that could be Turing complete in general and thus the equality itself is undecidable due to the halting problem
. Some type theories enforce the restriction that all computations be decidable so that definitional equality may be used.
In contrast in intensional Type Theory type checking is decidable
, but the representation of standard mathematical concepts is somewhat complex, since extensional reasoning requires using setoid
s or similar constructions. It is a subject of current discussion whether this tradeoff is unavoidable and whether the lack of extensional principles in intensional Type Theory is a feature or a bug.
, LEGO and Coq
. Recently, dependent types also featured in the design of programming languages such as ATS
, Cayenne, Epigram and Agda.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
based on the principles of mathematical constructivism. Intuitionistic type theory was introduced by Per Martin-Löf
Per Martin-Löf
Per Erik Rutger Martin-Löf is a Swedish logician, philosopher, and mathematical statistician. He is internationally renowned for his work on the foundations of probability, statistics, mathematical logic, and computer science. Since the late 1970s, Martin-Löf's publications have been mainly in...
, a Swedish
Sweden
Sweden , officially the Kingdom of Sweden , is a Nordic country on the Scandinavian Peninsula in Northern Europe. Sweden borders with Norway and Finland and is connected to Denmark by a bridge-tunnel across the Öresund....
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
and philosopher, in 1972. Martin-Löf has modified his proposal a few times; his 1971 impredicative
Impredicative
In mathematics and logic, impredicativity is the property of a self-referencing definition. More precisely, a definition is said to be impredicative if it invokes the set being defined, or another set which contains the thing being defined.Russell's paradox is a famous example of an impredicative...
formulation was inconsistent as demonstrated by Girard's paradox. Later formulations were predicative
Predicative
Predicative may mean:* Predicative * Predicative * Lacking impredicativity...
. He proposed both intensional
Intensional
Intensional* in philosophy of language: not extensional. See also intensional definition versus extensional definition.* in philosophy of mind: an intensional state is a state which has a propositional content....
and extensional
Extensionality
In logic, extensionality, or extensional equality refers to principles that judge objects to be equal if they have the same external properties...
variants of the theory.
Intuitionistic type theory is based on a certain analogy or isomorphism between proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s and types
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
: a proposition is identified with the type of its proofs. This identification is usually called the Curry–Howard isomorphism, which was originally formulated for intuitionistic logic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
and simply typed lambda calculus
Simply typed lambda calculus
The simply typed lambda calculus , a formof type theory, is a typed interpretation of the lambda calculus with only one type constructor: \to that builds function types. It is the canonical and simplest example of a typed lambda calculus...
. Type Theory extends this identification to predicate logic
Predicate logic
In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
by introducing dependent types, that is types which contain values.
Type Theory internalizes the interpretation of intuitionistic logic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
proposed by Brouwer
Luitzen Egbertus Jan Brouwer
Luitzen Egbertus Jan Brouwer FRS , usually cited as L. E. J. Brouwer but known to his friends as Bertus, was a Dutch mathematician and philosopher, a graduate of the University of Amsterdam, who worked in topology, set theory, measure theory and complex analysis.-Biography:Early in his career,...
, Heyting
Arend Heyting
Arend Heyting was a Dutch mathematician and logician. He was a student of Luitzen Egbertus Jan Brouwer at the University of Amsterdam, and did much to put intuitionistic logic on a footing where it could become part of mathematical logic...
and Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
, the so called BHK interpretation
BHK interpretation
In mathematical logic, the Brouwer–Heyting–Kolmogorov interpretation, or BHK interpretation, of intuitionistic logic was proposed by L. E. J. Brouwer, Arend Heyting and independently by Andrey Kolmogorov...
. The types of Type Theory play a similar role to sets in set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
but functions definable in Type Theory are always computable.
Connectives of Type Theory
In the context of Type Theory a connectiveLogical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
is a way of constructing types, possibly using already given types.
The basic connectives of Type Theory are:
Π-types
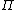 -types, also called dependent product types, are analogous to the indexed products
-types, also called dependent product types, are analogous to the indexed productsCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of sets. As such, they generalize the normal function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
to model functions whose result type may vary on their input. E.g. writing
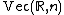 for
for  -tuples of real numbers,
-tuples of real numbers, 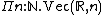 stands for the type of functions which given a natural number
stands for the type of functions which given a natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
returns a tuple of real numbers of this size. The usual function space arises as a special case when the range type does not actually depend on the input, e.g.
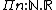 is the type of functions from natural numbers to the real numbers, which is also written as
is the type of functions from natural numbers to the real numbers, which is also written as 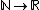 . Using the Curry–Howard isomorphism
. Using the Curry–Howard isomorphism 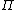 -types also serve to model implication
-types also serve to model implicationImplication
Implication may refer to:In logic:* Logical implication, entailment, or consequence, a relation between statements* Material implication, or conditional implication, a binary truth functionIn linguistics, specifically in pragmatics:...
and universal quantification
Universal quantification
In predicate logic, universal quantification formalizes the notion that something is true for everything, or every relevant thing....
: e.g. a term inhabiting
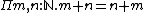 is a function which assigns to any pair of natural numbers a proof that addition is commutative for that pair and hence can be considered as a proof that addition is commutative for all natural numbers.
is a function which assigns to any pair of natural numbers a proof that addition is commutative for that pair and hence can be considered as a proof that addition is commutative for all natural numbers.Σ-types
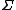 -types, also called dependent sum types, are analogous to the indexed disjoint union
-types, also called dependent sum types, are analogous to the indexed disjoint unionDisjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
s of sets. As such, they generalize the usual Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
to model pairs where the type of the 2nd component depends on the first. E.g. the type
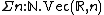 stands for the type of pairs of a natural number
stands for the type of pairs of a natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
and a tuple
Tuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
of real numbers of that size, i.e. this type can be used to model sequences of arbitrary length (usually called lists). The conventional Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
type arises as a special case when the type of the 2nd component doesn't actually depend on the first, e.g.
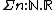 is the type of pairs of a natural number
is the type of pairs of a natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
and a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, which is also written as
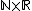 . Again, using the Curry–Howard isomorphism,
. Again, using the Curry–Howard isomorphism, 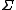 -types also serve to model conjunction
-types also serve to model conjunctionConjunction
Conjunction can refer to:* Conjunction , an astronomical phenomenon* Astrological aspect, an aspect in horoscopic astrology* Conjunction , a part of speech** Conjunctive mood , same as subjunctive mood...
and existential quantification
Existential quantification
In predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
.
Finite types
Of special importance are 0 or ⊥ (the empty type), 1 or ⊤ (the unit typeUnit type
In the area of mathematical logic, and computer science known as type theory, a unit type is a type that allows only one value . The carrier associated with a unit type can be any singleton set. There is an isomorphism between any two such sets, so it is customary to talk about the unit type and...
) and 2 (the type of Booleans or classical truth values). Invoking the Curry–Howard isomorphism again, ⊥ stands for False and ⊤ for True.
Using finite types we can define negation
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
as
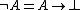 .
.Equality type
Given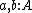 then
then 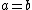 is the type of equality proofs that
is the type of equality proofs that  is equal to
is equal to 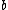 . There is only one (canonical) inhabitant of
. There is only one (canonical) inhabitant of  and this is the proof of reflexivity
and this is the proof of reflexivity 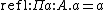 .
.Inductive types
A prime example of an inductive type is the type of natural numbers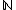 which is generated by
which is generated by 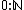 and
and 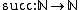 . An important application of the propositions as types principle is the identification of (dependent) primitive recursion and induction
. An important application of the propositions as types principle is the identification of (dependent) primitive recursion and inductionMathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
by one elimination constant:
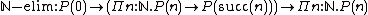 for any given type
for any given type 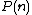 indexed by
indexed by 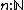 . In general inductive types can be defined in terms of W-types, the type of well-founded trees.
. In general inductive types can be defined in terms of W-types, the type of well-founded trees.An important class of inductive types are inductive families like the type of vectors
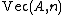 mentioned above, which is inductively generated by the constructors
mentioned above, which is inductively generated by the constructors 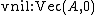 and
and 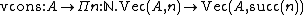 . Applying the Curry–Howard isomorphism once more, inductive families correspond to inductively defined relations.
. Applying the Curry–Howard isomorphism once more, inductive families correspond to inductively defined relations.Universes
An example of a universe is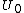 , the universe of all small types, which contains names for all the types introduced so far. To every name
, the universe of all small types, which contains names for all the types introduced so far. To every name 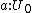 we associate a type
we associate a type 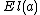 , its extension or meaning. It is standard to assume a predicative hierarchy of universes:
, its extension or meaning. It is standard to assume a predicative hierarchy of universes: 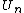 for every natural number
for every natural number 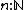 , where the universe
, where the universe 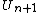 contains a code for the previous universe, i.e. we have
contains a code for the previous universe, i.e. we have 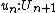 with
with 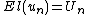 . This hierarchy is often assumed to be cumulative, that is the codes from
. This hierarchy is often assumed to be cumulative, that is the codes from 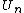 are embedded in
are embedded in 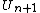 .
.Stronger universe principles have been investigated, i.e. super universes and the Mahlo universe. In 1992 Huet and Coquand introduced the calculus of constructions
Calculus of constructions
The calculus of constructions is a formal language in which both computer programs and mathematical proofs can be expressed. This language forms the basis of theory behind the Coq proof assistant, which implements the derivative calculus of inductive constructions.-General traits:The CoC is a...
, a type theory with an impredicative universe, thus combining Type Theory with Girard
Jean-Yves Girard
Jean-Yves Girard is a French logician working in proof theory. His contributions include a proof of strong normalization in a system of second-order logic called system F; the invention of linear logic; the geometry of interaction; and ludics...
's System F
System F
System F, also known as the polymorphic lambda calculus or the second-order lambda calculus, is a typed lambda calculus that differs from the simply typed lambda calculus by the introduction of a mechanism of universal quantification over types...
. This extension is not universally accepted by Intuitionists since it allows impredicative, i.e. circular, constructions, which are often identified with classical reasoning.
Formalisation of Type Theory
Type Theory is usually presented as a dependently typed lambda calculusTyped lambda calculus
A typed lambda calculus is a typed formalism that uses the lambda-symbol to denote anonymous function abstraction. In this context, types are usually objects of a syntactic nature that are assigned to lambda terms; the exact nature of a type depends on the calculus considered...
, using the judgements:
-
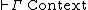 ,
, 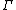 is a well-formed context of typing assumptions.
is a well-formed context of typing assumptions. -
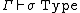 ,
,  is a well-formed type in context
is a well-formed type in context 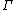 .
. -
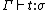 ,
,  is a well-formed term of type
is a well-formed term of type  in context
in context 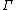 .
. -
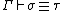 ,
,  and
and  are equal types in context
are equal types in context 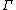 .
. -
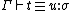 ,
,  and
and  are equal terms of type
are equal terms of type  in context
in context 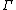 .
.
Of special importance is the conversion rule, which says that given
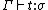 and
and 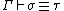 then
then 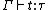 .
.Categorical models of Type Theory
Using the language of category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, R.A.G. Seely introduced the notion of a locally cartesian closed category (LCCC) as the basic model of Type Theory. This has been refined by Hofmann and Dybjer to Categories with Families or Categories with Attributes based on earlier work by Cartmell.
A category with families is a category C of contexts (in which the objects are contexts, and
the context morphisms are substitutions), together with a functor T : Cop → Fam(Set).
Fam(Set) is the category of families of Sets, in which objects are pairs (A,B) of an "index set" A and a function B: X → A, and morphisms are pairs of functions f : A → A' and g : X → X' , such that B' ° g = f ° B - in other words, f maps Ba to B'g(a).
The functor T assigns to a context G a set Ty(G) of types, and for each A : Ty(G), a set Tm(G,A) of terms.
The axioms for a functor require that these play harmoniously with substitution. Substitution is usually
written in the form Af or af, where A is a type in Ty(G) and a is a term in Tm(G,A), and f is a substitution
from D to G. Here Af : Ty(D) and af : Tm(D,Af).
The category C must contain a terminal object (the empty context), and a final object for a form
of product called comprehension, or context extension, in which the right element is a type in the context of the left element.
If G is a context, and A : Ty(G), then there should be an object (G,A) final among
contexts D with mappings p : D → G, q : Tm(D,Ap).
A logical framework, such as Martin-Löf's takes the form of
closure conditions on the context dependent sets of types and terms: that there should be a type called
Set, and for each set a type, that the types should be closed under forms of dependent sum and
product, and so forth.
A theory such as that of predicative set theory expresses closure conditions on the types of sets and
their elements: that they should be closed under operations that reflect dependent sum and product,
and under various forms of inductive definition.
Extensional versus intensional
A fundamental distinction is extensionalExtensional definition
An extensional definition of a concept or term formulates its meaning by specifying its extension, that is, every object that falls under the definition of the concept or term in question....
vs intensional
Intensional definition
In logic and mathematics, an intensional definition gives the meaning of a term by specifying all the properties required to come to that definition, that is, the necessary and sufficient conditions for belonging to the set being defined....
Type Theory. In extensional Type Theory definitional (i.e. computational) equality is not distinguished from propositional equality, which requires proof. As a consequence type checking becomes undecidable
Undecidable
Undecidable may refer to:In mathematics and logic* Undecidable problem - a decision problem which no algorithm can decide* "Undecidable" is sometimes used as a synonym of "independent", where a formula in mathematical logic is independent of a logical theory if neither that formula nor its negation...
in extensional type theory. This is because relying on computational equality means that the equality depends on computations that could be Turing complete in general and thus the equality itself is undecidable due to the halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
. Some type theories enforce the restriction that all computations be decidable so that definitional equality may be used.
In contrast in intensional Type Theory type checking is decidable
Decidable
The word decidable may refer to:* Decidable language*Decidability for the equivalent in mathematical logic*Gödel's incompleteness theorem, a theorem on the indecidability of languages consisting of "true statements" in mathematical logic....
, but the representation of standard mathematical concepts is somewhat complex, since extensional reasoning requires using setoid
Setoid
In mathematics, a setoid is a set equipped with an equivalence relation.Setoids are studied especially in proof theory and in type-theoretic foundations of mathematics. Often in mathematics, when one defines an equivalence relation on a set, one immediately forms the quotient set...
s or similar constructions. It is a subject of current discussion whether this tradeoff is unavoidable and whether the lack of extensional principles in intensional Type Theory is a feature or a bug.
Implementations of Type Theory
Type Theory has been the base of a number of proof assistants, such as NuPRLNuPRL
NuPRL is a higher-order proof development system developed at Cornell University. It was founded by Joseph L. Bates and Robert L. Constable in 1979 and, since then, many have contributed to the development of NuPRL....
, LEGO and Coq
Coq
In computer science, Coq is an interactive theorem prover. It allows the expression of mathematical assertions, mechanically checks proofs of these assertions, helps to find formal proofs, and extracts a certified program from the constructive proof of its formal specification...
. Recently, dependent types also featured in the design of programming languages such as ATS
ATS (programming language)
ATS is a programming language whose stated purpose is to support theorem proving in combination with practical programming through the use of advanced type systems. The performance of ATS has been demonstrated to be comparable to that of the C and C++ programming languages...
, Cayenne, Epigram and Agda.
See also
- Calculus of constructionsCalculus of constructionsThe calculus of constructions is a formal language in which both computer programs and mathematical proofs can be expressed. This language forms the basis of theory behind the Coq proof assistant, which implements the derivative calculus of inductive constructions.-General traits:The CoC is a...
- Curry–Howard isomorphismCurry–HowardIn programming language theory and proof theory, the Curry–Howard correspondence is the direct relationship between computer programs and proofs...
- Intuitionistic logicIntuitionistic logicIntuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
- Martin-Löf, PerPer Martin-LöfPer Erik Rutger Martin-Löf is a Swedish logician, philosopher, and mathematical statistician. He is internationally renowned for his work on the foundations of probability, statistics, mathematical logic, and computer science. Since the late 1970s, Martin-Löf's publications have been mainly in...
- Type theoryType theoryIn mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
- Typed lambda calculusTyped lambda calculusA typed lambda calculus is a typed formalism that uses the lambda-symbol to denote anonymous function abstraction. In this context, types are usually objects of a syntactic nature that are assigned to lambda terms; the exact nature of a type depends on the calculus considered...
Further reading
- Bengt Nordström; Kent Petersson; Jan M. Smith (1990). Programming in Martin-Löf's Type Theory. Oxford University Press. The book is out of print, but a free version can be picked up from here.
- Thompson, Simon (1991). Type Theory and Functional Programming Addison-Wesley. ISBN 0-201-41667-0.
- Granström, Johan G. (2011). Treatise on Intuitionistic Type Theory Springer. ISBN 978-94-007-1735-0.
External links
- EU Types Project: Tutorials - lecture notes and slides from the Types Summer School 2005
- n-Categories - Sketch of a Definition - letter from John Baez and James Dolan to Ross Street, Nov. 29, 1995

