
Categorial grammar
Encyclopedia
Categorial grammar is a term used for a family of formalisms in natural language
syntax
motivated by the principle of compositionality and organized according to the view that syntactic constituents should generally combine as function
s or according to a function-argument relationship. Most versions of Categorial Grammar are phrase structure grammars
, as opposed to dependency grammars
.
A categorial grammar shares some features with the simply typed lambda calculus
.
Whereas the lambda calculus
has only one function type ,
,
a categorial grammar typically has two function types, one type which is applied on the left,
one on the right. For example, a simple categorial grammar might have two function types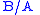 and
and 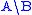 .
.
The first, , is the type of a phrase that results in a phrase of type
, is the type of a phrase that results in a phrase of type
 when followed (on the right) by a phrase of type
when followed (on the right) by a phrase of type  .
.
The second,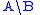 , is the type of a phrase that results
, is the type of a phrase that results
in a phrase of type when preceded (on the left) by a phrase of type
when preceded (on the left) by a phrase of type
 .
.
As Lambek explains, the notation is based upon algebra.
A fraction when multiplied by (i.e. concatenated with) its denominator yields its numerator.
Since concatenation is not commutative,
it makes difference whether the denominator occurs to the left or right.
The concatenation must be on the same side as the denominator for it to cancel out.
The first and simplest kind of categorial grammar is called a basic
categorial grammar, or sometimes an AB-grammar (after Ajdukiewicz and
Bar-Hillel).
Given a set of primitive types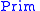 , let
, let
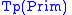 be the set of types constructed
be the set of types constructed
from primitive types. In the basic case, this is the least set
such that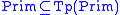
and if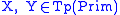
then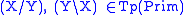 .
.
Think of these as purely formal expressions freely generated from the
primitive types; any semantics will be added later. Some authors
assume a fixed infinite set of primitive types used by all grammars,
but by making the primitive types part of the grammar,
the whole construction is kept finite.
A basic categorial grammar is a tuple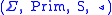
where is a finite set of symbols,
is a finite set of symbols,
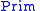 is a finite set of primitive types,
is a finite set of primitive types,
and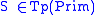 .
.
The relation is the lexicon, which relates types
is the lexicon, which relates types
to symbols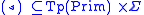 .
.
Since the lexicon is finite, it can be specifed by listing
a set of pairs like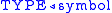 .
.
Such a grammar for English might have three basic types
 , assigning
, assigning
count noun
s the type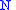 , complete noun phrases the type
, complete noun phrases the type
 , and sentences the type
, and sentences the type  .
.
Then an adjective
could have the type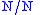 ,
,
because if it is followed by a noun then the whole phrase is a noun.
Similarly, a determiner has the type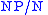 ,
,
because it forms a complete noun phrase when followed by a noun.
Intransitive verb
s have the type
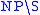 , and transitive verbs the type
, and transitive verbs the type 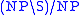 .
.
Then a string of words is a sentence if it has overall type .
.
For example, take the string "the bad boy made that mess". Now "the"
and "that" are determiners, "boy" and "mess" are nouns, "bad" is an
adjective, and "made" is a transitive verb, so the lexicon is
{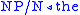 ,
,
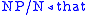 ,
,
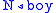 ,
,
 ,
,
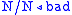 ,
,
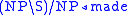 }.
}.
and the sequence of types in the string is
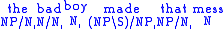
now find functions and appropriate arguments and reduce them
according to the two rules
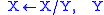 and
and
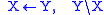 :
:
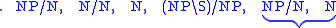
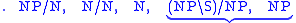

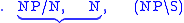
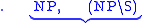

The fact that the result is means that the string is a sentence, while the sequence of reductions shows that it must be parsed as ((the (bad boy)) (made (that mess))).
means that the string is a sentence, while the sequence of reductions shows that it must be parsed as ((the (bad boy)) (made (that mess))).
Categorial grammars of this form (having only function application rules) are equivalent in generative capacity to context-free grammar
s and are thus often considered inadequate for theories of natural language syntax. Unlike CFGs, categorial grammars are lexicalized, meaning that only a small number of (mostly language-independent) rules are employed, and all other syntactic phenomena derive from the lexical entries of specific words.
Another appealing aspect of categorial grammars is that it is often easy to assign them a compositional semantics, by first assigning interpretation types to all the basic categories, and then associating all the derived categories
with appropriate function
types. The interpretation of any constituent is then simply the value of a function at an argument. With some modifications to handle intensionality and quantification
, this approach can be used to cover a wide variety of semantic phenomena.
concatenation operator for types, and several other inference rules.
Pentus has shown that these still have the generative capacity of
context-free grammars.
For the Lambek calculus, there is a type concatenation
operator , so
, so
that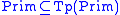
and if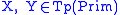
then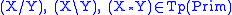 .
.
The Lambek calculus consists of several deduction rules which specify
how type inclusion assertions can be derived. In the following
rules, upper case roman letters stand for types, upper case Greek
letters stand for sequences of types. A sequent of the form

can be read: a string is of type if it consists of the concatenation
if it consists of the concatenation
of strings of each of the types in . If a type is
. If a type is
interpreted as a set of strings, then the
 may be interpreted as
may be interpreted as  ,
,
that is, "includes as a subset".
A horizontal line means that the inclusion above the line
implies the one below the line.
The process is begun by the Axiom rule, which as no antecedents and
just says that any type includes itself.
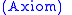
The Cut rule says that inclusions can be composed.
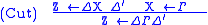
The other rules come in pairs, one pair for each type construction
operator, each pair consisting of one rule for the operator in the
target, one in the source, of the arrow.
The name of a rule consists of the operator and an arrow, with the
operator on the side of the arrow on which it occurs in the conclusion.
For an example, here is a derivation of "type raising", which says that
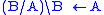 . The names of rules and the substitutions used are to the right.
. The names of rules and the substitutions used are to the right.
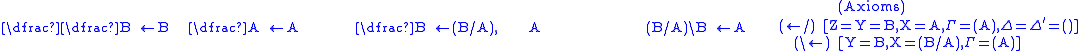
is a 4-tuple:
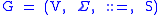
where
1. is a finite set of non-terminals or variables.
is a finite set of non-terminals or variables.
2. is a finite set of terminal symbols.
is a finite set of terminal symbols.
3. is a finite set of production rules, that is, a finite relation
is a finite set of production rules, that is, a finite relation
 .
.
4. is the start variable.
is the start variable.
From the point of view of categorial grammars, a context-free grammar
can be seen as a calculus with a set of special purpose axioms for
each language, but with no type construction operators and no
inference rules except Cut.
Specifically, given a context-free grammar as above, define a categorial
grammar
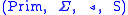
where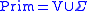 ,
,
and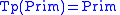 .
.
Let there be an axiom
 for every symbol
for every symbol
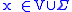 ,
,
an axiom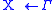
for every production rule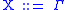 ,
,
a lexicon entry for every terminal symbol
for every terminal symbol
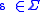 ,
,
and Cut for the only rule.
This categorial grammar generates the same language as the given CFG.
Of course, this is not a basic categorial grammar, since it has
special axioms that depend upon the language; i.e. it is not lexicalized.
Also, it makes no use at all of non-primitive types.
To show that any context-free language can be generated by
a basic categorial grammar, recall that
any context-free language can be generated by a context-free grammar
in Greibach normal form
.
The grammar is in Greibach normal form if every production rule is
of the form
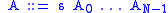 ,
,
where capital letters are variables,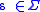 ,
,
and ,
,
that is, the right side of the production is a single terminal symbol
followed by zero or more (non-terminal) variables.
Now given a CFG in Greibach normal form,
define a basic categorial grammar with a primitive type
for each non-terminal variable
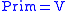 ,
,
and with an entry in the lexicon
 ,
,
for each production rule
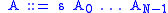 .
.
It is fairly easy to see that this basic categorial grammar
generates the same language as the original CFG.
Note that the lexicon of this grammar will generally
assign multiple types to each symbol.
The same construction works for Lambek grammars, since
they are an extension of basic categorial grammars.
It is necessary to verify that the extra inference rules
do not change the generated language. This can be done
and shows that every context-free language is generated
by some Lambek grammar.
To show the converse, that every language generated by a
Lambek grammar is context-free, is much more difficult.
It was an open problem for nearly thirty years, from
the early 1960s until about 1991 when it was proven
by Pentus.
The basic idea is, given a Lambek grammar,
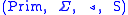
construct a context-free grammar

with the same set of terminal symbols, the
same start symbol, with variables some (not all) types
 ,
,
and with a production rule
for each entry

in the lexicon,
and production rules
for certain sequents
which are derivable in the Lambek calculus.
Of course, there are infinitely many types
and infinitely many derivable sequents, so in
order to make a finite grammar it is necessary
put a bound on the size of the types and sequents
that are needed. The heart of Pentus's proof
is to show that there is such a finite bound.
formal language theory, logic, category theory, and linguistics, conflict
with each other. In logic, arrows point to the more general from the more particular,
that is, to the conclusion from the hypotheses. In this article,
this convention is followed, i.e. the target of the arrow is the more general (inclusive) type.
In logic, arrows usually point left to right. In this article this convention is
reversed for consistency with the notation of context-free grammars, where the
single non-terminal symbol is always on the left. We use the symbol
in a production rule as in Backus-Naur form. Some authors use an arrow, which
unfortunately may point in either direction, depending on whether the grammar is
thought of as generating or recognizing the language.
Some authors on categorial grammars write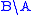 instead of
instead of
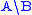 . The convention used here follows Lambek and algebra.
. The convention used here follows Lambek and algebra.
(in 1935) and Yehoshua Bar-Hillel
(in 1953). In 1958, Joachim Lambek
introduced a syntactic calculus that formalized the function type constructors along with various rules for the combination of functions. This calculus is a forerunner of
linear logic
in that it is a substructural logic
. Montague grammar
uses an ad hoc syntactic system for English that is based on the principles of categorial grammar. Although Montague's
work is sometimes regarded as syntactically uninteresting, it helped to bolster interest in categorial grammar by associating it with a highly successful formal treatment of natural language semantics
. More recent work in categorial grammar has focused on the improvement of syntactic coverage. One formalism which has received considerable attention in recent years is Steedman
and Szabolcsi
's combinatory categorial grammar
which builds on combinatory logic
invented by Moses Schönfinkel
and Haskell Curry
.
There are a number of related formalisms of this kind in linguistics, such as type logical grammar and abstract categorial grammar.
A derivation is a binary tree that encodes a proof.
A derivation can be displayed as a parse tree, showing the syntactic structure of a sentence.
In a right (left) function application, the node of the type A\B (B/A) is called the functor, and the node of the type A is called an argument.
, gender
, number
, and tense
. Sometimes only atomic categories are tagged in this way. In Montague grammar, it is traditional to subdivide function categories using a multiple slash convention, so A/B and A//B would be two distinct categories of left-applying functions, that took the same arguments but could be distinguished between by other functions taking them as arguments.
and extraction
, especially as they relate to phenomena like right node raising. The introduction of function composition into a categorial grammar leads to many kinds of derivational ambiguity that are vacuous in the sense that they do not correspond to semantic ambiguities.
Natural language
In the philosophy of language, a natural language is any language which arises in an unpremeditated fashion as the result of the innate facility for language possessed by the human intellect. A natural language is typically used for communication, and may be spoken, signed, or written...
syntax
Syntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
motivated by the principle of compositionality and organized according to the view that syntactic constituents should generally combine as function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s or according to a function-argument relationship. Most versions of Categorial Grammar are phrase structure grammars
Phrase structure grammar
The term phrase structure grammar was originally introduced by Noam Chomsky as the term for grammars as defined by phrase structure rules, i.e. rewrite rules of the type studied previously by Emil Post and Axel Thue...
, as opposed to dependency grammars
Dependency grammar
Dependency grammar is a class of modern syntactic theories that are all based on the dependency relation and that can be traced back primarily to the work of Lucien Tesnière. Dependency grammars are distinct from phrase structure grammars , since they lack phrasal nodes. Structure is determined by...
.
Basics of categorial grammar
A categorial grammar consists of two parts, a lexicon, which assigns a set of types (also called categories) to each basic symbol, and some type inference rules, which determine how the type of a string of symbols follows from the types of the constituent symbols. It has the advantage that the type inference rules can be fixed once and for all, so that the specification of a particular language grammar is entirely determined by the lexicon.A categorial grammar shares some features with the simply typed lambda calculus
Simply typed lambda calculus
The simply typed lambda calculus , a formof type theory, is a typed interpretation of the lambda calculus with only one type constructor: \to that builds function types. It is the canonical and simplest example of a typed lambda calculus...
.
Whereas the lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
has only one function type
 ,
,a categorial grammar typically has two function types, one type which is applied on the left,
one on the right. For example, a simple categorial grammar might have two function types
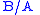 and
and 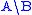 .
.The first,
 , is the type of a phrase that results in a phrase of type
, is the type of a phrase that results in a phrase of type when followed (on the right) by a phrase of type
when followed (on the right) by a phrase of type  .
.The second,
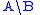 , is the type of a phrase that results
, is the type of a phrase that resultsin a phrase of type
 when preceded (on the left) by a phrase of type
when preceded (on the left) by a phrase of type .
.As Lambek explains, the notation is based upon algebra.
A fraction when multiplied by (i.e. concatenated with) its denominator yields its numerator.
Since concatenation is not commutative,
it makes difference whether the denominator occurs to the left or right.
The concatenation must be on the same side as the denominator for it to cancel out.
The first and simplest kind of categorial grammar is called a basic
categorial grammar, or sometimes an AB-grammar (after Ajdukiewicz and
Bar-Hillel).
Given a set of primitive types
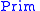 , let
, let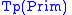 be the set of types constructed
be the set of types constructedfrom primitive types. In the basic case, this is the least set
such that
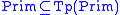
and if
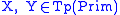
then
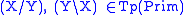 .
.Think of these as purely formal expressions freely generated from the
primitive types; any semantics will be added later. Some authors
assume a fixed infinite set of primitive types used by all grammars,
but by making the primitive types part of the grammar,
the whole construction is kept finite.
A basic categorial grammar is a tuple
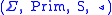
where
 is a finite set of symbols,
is a finite set of symbols,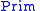 is a finite set of primitive types,
is a finite set of primitive types,and
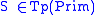 .
.The relation
 is the lexicon, which relates types
is the lexicon, which relates typesto symbols
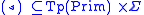 .
.Since the lexicon is finite, it can be specifed by listing
a set of pairs like
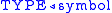 .
.Such a grammar for English might have three basic types
 , assigning
, assigningcount noun
Count noun
In linguistics, a count noun is a common noun that can be modified by a numeral and that occurs in both singular and plural form, as well as co-occurring with quantificational determiners like every, each, several, etc. A mass noun has none of these properties...
s the type
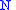 , complete noun phrases the type
, complete noun phrases the type , and sentences the type
, and sentences the type  .
.Then an adjective
Adjective
In grammar, an adjective is a 'describing' word; the main syntactic role of which is to qualify a noun or noun phrase, giving more information about the object signified....
could have the type
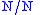 ,
,because if it is followed by a noun then the whole phrase is a noun.
Similarly, a determiner has the type
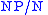 ,
,because it forms a complete noun phrase when followed by a noun.
Intransitive verb
Verb
A verb, from the Latin verbum meaning word, is a word that in syntax conveys an action , or a state of being . In the usual description of English, the basic form, with or without the particle to, is the infinitive...
s have the type
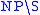 , and transitive verbs the type
, and transitive verbs the type 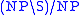 .
.Then a string of words is a sentence if it has overall type
 .
.For example, take the string "the bad boy made that mess". Now "the"
and "that" are determiners, "boy" and "mess" are nouns, "bad" is an
adjective, and "made" is a transitive verb, so the lexicon is
{
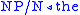 ,
,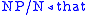 ,
,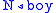 ,
, ,
,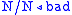 ,
,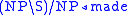 }.
}.and the sequence of types in the string is
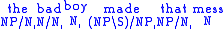
now find functions and appropriate arguments and reduce them
according to the two rules
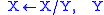 and
and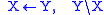 :
: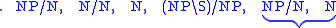
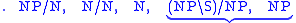

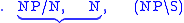
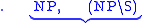

The fact that the result is
 means that the string is a sentence, while the sequence of reductions shows that it must be parsed as ((the (bad boy)) (made (that mess))).
means that the string is a sentence, while the sequence of reductions shows that it must be parsed as ((the (bad boy)) (made (that mess))).Categorial grammars of this form (having only function application rules) are equivalent in generative capacity to context-free grammar
Context-free grammar
In formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
s and are thus often considered inadequate for theories of natural language syntax. Unlike CFGs, categorial grammars are lexicalized, meaning that only a small number of (mostly language-independent) rules are employed, and all other syntactic phenomena derive from the lexical entries of specific words.
Another appealing aspect of categorial grammars is that it is often easy to assign them a compositional semantics, by first assigning interpretation types to all the basic categories, and then associating all the derived categories
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
with appropriate function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
types. The interpretation of any constituent is then simply the value of a function at an argument. With some modifications to handle intensionality and quantification
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
, this approach can be used to cover a wide variety of semantic phenomena.
Lambek Calculus
A Lambek grammar is an elaboration of this idea which has aconcatenation operator for types, and several other inference rules.
Pentus has shown that these still have the generative capacity of
context-free grammars.
For the Lambek calculus, there is a type concatenation
operator
 , so
, sothat
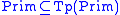
and if
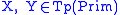
then
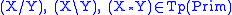 .
.The Lambek calculus consists of several deduction rules which specify
how type inclusion assertions can be derived. In the following
rules, upper case roman letters stand for types, upper case Greek
letters stand for sequences of types. A sequent of the form

can be read: a string is of type
 if it consists of the concatenation
if it consists of the concatenationof strings of each of the types in
 . If a type is
. If a type isinterpreted as a set of strings, then the
 may be interpreted as
may be interpreted as  ,
,that is, "includes as a subset".
A horizontal line means that the inclusion above the line
implies the one below the line.
The process is begun by the Axiom rule, which as no antecedents and
just says that any type includes itself.
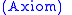
The Cut rule says that inclusions can be composed.
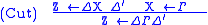
The other rules come in pairs, one pair for each type construction
operator, each pair consisting of one rule for the operator in the
target, one in the source, of the arrow.
The name of a rule consists of the operator and an arrow, with the
operator on the side of the arrow on which it occurs in the conclusion.
| Target | Source |
|---|---|
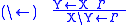 |
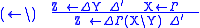 |
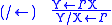 |
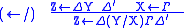 |
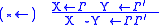 |
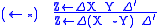 |
For an example, here is a derivation of "type raising", which says that
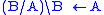 . The names of rules and the substitutions used are to the right.
. The names of rules and the substitutions used are to the right.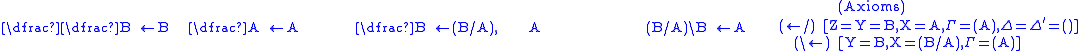
Relation to Context Free Grammars
Recall that a context-free grammarContext-free grammar
In formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
is a 4-tuple:
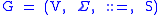
where
1.
 is a finite set of non-terminals or variables.
is a finite set of non-terminals or variables.2.
 is a finite set of terminal symbols.
is a finite set of terminal symbols.3.
 is a finite set of production rules, that is, a finite relation
is a finite set of production rules, that is, a finite relation .
.4.
 is the start variable.
is the start variable.From the point of view of categorial grammars, a context-free grammar
can be seen as a calculus with a set of special purpose axioms for
each language, but with no type construction operators and no
inference rules except Cut.
Specifically, given a context-free grammar as above, define a categorial
grammar
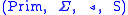
where
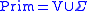 ,
,and
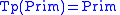 .
.Let there be an axiom
 for every symbol
for every symbol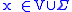 ,
,an axiom
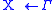
for every production rule
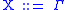 ,
,a lexicon entry
 for every terminal symbol
for every terminal symbol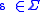 ,
,and Cut for the only rule.
This categorial grammar generates the same language as the given CFG.
Of course, this is not a basic categorial grammar, since it has
special axioms that depend upon the language; i.e. it is not lexicalized.
Also, it makes no use at all of non-primitive types.
To show that any context-free language can be generated by
a basic categorial grammar, recall that
any context-free language can be generated by a context-free grammar
in Greibach normal form
Greibach normal form
In computer science and formal language theory, a context-free grammar is in Greibach normal form if the right-hand sides of all productions start with a terminal symbol, optionally followed by some variables. A non-strict form allows one exception to this format restriction for allowing the empty...
.
The grammar is in Greibach normal form if every production rule is
of the form
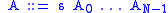 ,
,where capital letters are variables,
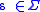 ,
,and
 ,
,that is, the right side of the production is a single terminal symbol
followed by zero or more (non-terminal) variables.
Now given a CFG in Greibach normal form,
define a basic categorial grammar with a primitive type
for each non-terminal variable
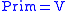 ,
,and with an entry in the lexicon
 ,
,for each production rule
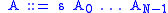 .
.It is fairly easy to see that this basic categorial grammar
generates the same language as the original CFG.
Note that the lexicon of this grammar will generally
assign multiple types to each symbol.
The same construction works for Lambek grammars, since
they are an extension of basic categorial grammars.
It is necessary to verify that the extra inference rules
do not change the generated language. This can be done
and shows that every context-free language is generated
by some Lambek grammar.
To show the converse, that every language generated by a
Lambek grammar is context-free, is much more difficult.
It was an open problem for nearly thirty years, from
the early 1960s until about 1991 when it was proven
by Pentus.
The basic idea is, given a Lambek grammar,
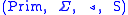
construct a context-free grammar

with the same set of terminal symbols, the
same start symbol, with variables some (not all) types
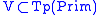 ,
,and with a production rule
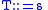
for each entry

in the lexicon,
and production rules

for certain sequents

which are derivable in the Lambek calculus.
Of course, there are infinitely many types
and infinitely many derivable sequents, so in
order to make a finite grammar it is necessary
put a bound on the size of the types and sequents
that are needed. The heart of Pentus's proof
is to show that there is such a finite bound.
Notation
The notation in this field is not standardized. The notations used informal language theory, logic, category theory, and linguistics, conflict
with each other. In logic, arrows point to the more general from the more particular,
that is, to the conclusion from the hypotheses. In this article,
this convention is followed, i.e. the target of the arrow is the more general (inclusive) type.
In logic, arrows usually point left to right. In this article this convention is
reversed for consistency with the notation of context-free grammars, where the
single non-terminal symbol is always on the left. We use the symbol

in a production rule as in Backus-Naur form. Some authors use an arrow, which
unfortunately may point in either direction, depending on whether the grammar is
thought of as generating or recognizing the language.
Some authors on categorial grammars write
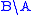 instead of
instead of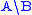 . The convention used here follows Lambek and algebra.
. The convention used here follows Lambek and algebra.Historical notes
The basic ideas of categorial grammar date from work by Kazimierz AjdukiewiczKazimierz Ajdukiewicz
Kazimierz Ajdukiewicz was a Polish philosopher and logician, a prominent figure in the Lwów–Warsaw school of logic. He originated many novel ideas in semiotics, including the "categorial grammar" used by many formal linguists...
(in 1935) and Yehoshua Bar-Hillel
Yehoshua Bar-Hillel
Yehoshua Bar-Hillel was an Israeli philosopher, mathematician, and linguist at the Hebrew University of Jerusalem, best known for his pioneering work in machine translation and formal linguistics.- Biography :...
(in 1953). In 1958, Joachim Lambek
Joachim Lambek
Joachim Lambek is Peter Redpath Emeritus Professor of Pure Mathematics at McGill University, where he earned his Ph.D. degree in 1950 with Hans Julius Zassenhaus as advisor. He is called Jim by his friends.- Scholarly work :...
introduced a syntactic calculus that formalized the function type constructors along with various rules for the combination of functions. This calculus is a forerunner of
linear logic
Linear logic
Linear logic is a substructural logic proposed by Jean-Yves Girard as a refinement of classical and intuitionistic logic, joining the dualities of the former with many of the constructive properties of the latter...
in that it is a substructural logic
Substructural logic
In logic, a substructural logic is a logic lacking one of the usual structural rules , such as weakening, contraction or associativity...
. Montague grammar
Montague grammar
Montague grammar is an approach to natural language semantics, named after American logician Richard Montague. The Montague grammar is based on formal logic, especially higher order predicate logic and lambda calculus, and makes use of the notions of intensional logic, via Kripke models...
uses an ad hoc syntactic system for English that is based on the principles of categorial grammar. Although Montague's
Richard Montague
Richard Merett Montague was an American mathematician and philosopher.-Career:At the University of California, Berkeley, Montague earned an B.A. in Philosophy in 1950, an M.A. in Mathematics in 1953, and a Ph.D. in Philosophy 1957, the latter under the direction of the mathematician and logician...
work is sometimes regarded as syntactically uninteresting, it helped to bolster interest in categorial grammar by associating it with a highly successful formal treatment of natural language semantics
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
. More recent work in categorial grammar has focused on the improvement of syntactic coverage. One formalism which has received considerable attention in recent years is Steedman
Mark Steedman
Mark Jerome Steedman, FBA, FRSE is a computational linguist and cognitive scientist.Steedman graduated from the University of Sussex in 1968, with a B.Sc in Experimental Psychology, and from the University of Edinburgh in 1973, with a Ph.D. in Artificial Intelligence Mark Jerome Steedman, FBA,...
and Szabolcsi
Anna Szabolcsi
Anna Szabolcsi is a linguist whose research has focused on semantics, syntax, and the syntax-semantics interface. She was born and educated in Hungary...
's combinatory categorial grammar
Combinatory categorial grammar
Combinatory categorial grammar is an efficiently parseable, yet linguistically expressive grammar formalism. It has a transparent interface between surface syntax and underlying semantic representation, including predicate-argument structure, quantification and information structure.CCG relies on...
which builds on combinatory logic
Combinatory logic
Combinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...
invented by Moses Schönfinkel
Moses Schönfinkel
Moses Ilyich Schönfinkel, also known as Moisei Isai'evich Sheinfinkel , was a Russian logician and mathematician, known for the invention of combinatory logic.- Life :Schönfinkel attended the Novorossiysk University of Odessa, studying mathematics under Samuil Osipovich...
and Haskell Curry
Haskell Curry
Haskell Brooks Curry was an American mathematician and logician. Curry is best known for his work in combinatory logic; while the initial concept of combinatory logic was based on a single paper by Moses Schönfinkel, much of the development was done by Curry. Curry is also known for Curry's...
.
There are a number of related formalisms of this kind in linguistics, such as type logical grammar and abstract categorial grammar.
Some definitions
- Derivation
A derivation is a binary tree that encodes a proof.
- Parse tree
A derivation can be displayed as a parse tree, showing the syntactic structure of a sentence.
- Functor and Argument
In a right (left) function application, the node of the type A\B (B/A) is called the functor, and the node of the type A is called an argument.
- Functor-argument structure
Refinements of categorial grammar
A variety of changes to categorial grammar have been proposed to improve syntactic coverage. Some of the most common ones are listed below.Features and subcategories
Most systems of categorial grammar subdivide categories. The most common way to do this is by tagging them with features, such as personGrammatical person
Grammatical person, in linguistics, is deictic reference to a participant in an event; such as the speaker, the addressee, or others. Grammatical person typically defines a language's set of personal pronouns...
, gender
Grammatical gender
Grammatical gender is defined linguistically as a system of classes of nouns which trigger specific types of inflections in associated words, such as adjectives, verbs and others. For a system of noun classes to be a gender system, every noun must belong to one of the classes and there should be...
, number
Grammatical number
In linguistics, grammatical number is a grammatical category of nouns, pronouns, and adjective and verb agreement that expresses count distinctions ....
, and tense
Grammatical tense
A tense is a grammatical category that locates a situation in time, to indicate when the situation takes place.Bernard Comrie, Aspect, 1976:6:...
. Sometimes only atomic categories are tagged in this way. In Montague grammar, it is traditional to subdivide function categories using a multiple slash convention, so A/B and A//B would be two distinct categories of left-applying functions, that took the same arguments but could be distinguished between by other functions taking them as arguments.
Function composition
Rules of function composition are included in many categorial grammars. An example of such a rule would be one that allowed the concatenation of a constituent of type A/B with one of type B/C to produce a new constituent of type A/C. The semantics of such a rule would simply involve the composition of the functions involved. Function composition is important in categorial accounts of conjunctionLogical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
and extraction
Extraction
Extraction may refer to:* Extraction , an album by guitarist Greg Howe* Extraction , the separation of a substance from a matrix* Extraction , the removal of someone from a hostile area to a secure location...
, especially as they relate to phenomena like right node raising. The introduction of function composition into a categorial grammar leads to many kinds of derivational ambiguity that are vacuous in the sense that they do not correspond to semantic ambiguities.
Conjunction
Many categorial grammars include a typical conjunction rule, of the general form X CONJ X → X, where X is a category. Conjunction can generally be applied to nonstandard constituents resulting from type raising or function composition..Discontinuity
The grammar is extended to handle linguistic phenomena such as discontinuous idioms, gapping and extraction.Further reading
- Michael Moortgat, Categorial Type Logics, Chapter 2 in J. van Benthem and A. ter Meulen (eds.) Handbook of Logic and Language. Elsevier, 1997, ISBN 0262220539
- Wojciech Buszkowski, Mathematical linguistics and proof theory, Chapter 12 in J. van Benthem and A. ter Meulen (eds.) Handbook of Logic and Language. Elsevier, 1997, ISBN 0262220539
External links
- Grammar, categorial at Springer Encyclopaedia of MathematicsEncyclopaedia of MathematicsThe Encyclopaedia of Mathematics is a large reference work in mathematics. It is available in book form and on CD-ROM....

