
Context-free grammar
Encyclopedia
In formal language theory, a context-free grammar (CFG)
is a formal grammar
in which every production rule
is of the form
where V is a single nonterminal symbol, and w is a string of terminal
s and/or nonterminals (w can be empty).
The language
s generated by context-free grammars are known as the context-free language
s.
Context-free grammars are important in linguistics
for describing the structure of sentences and words in natural language
, and in computer science
for describing the structure of programming language
s and other artificial languages.
In linguistics
, some authors use the term phrase structure grammar
to refer to context-free grammars, whereby phrase structure grammars are distinct from dependency grammars
. In computer science
, a popular notation for context-free grammars is Backus–Naur Form
, or BNF.
s of languages in terms of their block structure
, and described how sentences are recursively
built up from smaller phrases, and eventually individual words or word elements.
An essential property of these block structures is that logical units never overlap. For example, the sentence:
can be logically parenthesized as follows:
A context-free grammar provides a simple and mathematically precise mechanism for describing the methods by which phrases in some natural language are built from smaller blocks, capturing the "block structure" of sentences in a natural way. Its simplicity makes the formalism amenable to rigorous mathematical study. Important features of natural language syntax such as agreement
and reference
are not part of the context-free grammar, but the basic recursive structure of sentences, the way in which clauses nest inside other clauses, and the way in which lists of adjectives and adverbs are swallowed by nouns and verbs, is described exactly.
The formalism of context-free grammars was developed in the mid-1950s by Noam Chomsky
, and also their classification as a special type
of formal grammar
(which he called phrase-structure grammars).
In Chomsky's generative grammar
framework, the syntax of natural language was described by a context-free rules combined with transformation rules.
In later work (e.g. Chomsky 1981), the idea of formulating a grammar consisting of explicit rewrite rules was abandoned. In other generative frameworks, e.g. Generalized Phrase Structure Grammar (Gazdar et al. 1985), context-free grammars were taken to be the mechanism for the entire syntax, eliminating transformations.
Block structure was introduced into computer programming language
s by the Algol project (1957-1960), which, as a consequence, also featured a context-free grammar to describe the resulting Algol syntax. This became a standard feature of computer languages, and the notation for grammars used in concrete descriptions of computer languages came to be known as Backus-Naur Form, after two members of the Algol language design committee.
The "block structure" aspect that context-free grammars capture is so fundamental to grammar that the terms syntax and grammar are often identified with context-free grammar rules, especially in computer science. Formal constraints not captured by the grammar are then considered to be part of the "semantics" of the language.
Context-free grammars are simple enough to allow the construction of efficient parsing algorithms which, for a given string, determine whether and how it can be generated from the grammar. An Earley parser
is an example of such an algorithm, while the widely used LR
and LL parser
s are simpler algorithms that deal only with more restrictive subsets of context-free grammars.
:
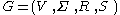
where
1.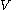 is a finite set; each element
is a finite set; each element 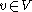 is called a non-terminal character or a variable. Each variable represents a different type of phrase or clause in the sentence. Variables are also sometimes called syntactic categories. Each variable defines a sub-language of the language defined by
is called a non-terminal character or a variable. Each variable represents a different type of phrase or clause in the sentence. Variables are also sometimes called syntactic categories. Each variable defines a sub-language of the language defined by 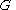 .
.
2.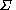 is a finite set of terminals, disjoint from
is a finite set of terminals, disjoint from 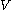 , which make up the actual content of the sentence. The set of terminals is the alphabet of the language defined by the grammar
, which make up the actual content of the sentence. The set of terminals is the alphabet of the language defined by the grammar 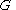 .
.
3.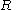 is a finite relation from
is a finite relation from 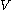 to
to 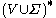 . The members of
. The members of 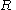 are called the (rewrite) rules or productions of the grammar. (also commonly symbolized by a
are called the (rewrite) rules or productions of the grammar. (also commonly symbolized by a 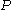 )
)
4.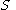 is the start variable (or start symbol), used to represent the whole sentence (or program). It must be an element of
is the start variable (or start symbol), used to represent the whole sentence (or program). It must be an element of 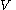 .
.
The asterisk represents the Kleene star
operation.
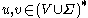 , we say
, we say 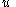 yields
yields 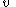 , written as
, written as 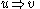 , if
, if 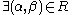 with
with 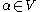 and
and 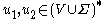 such that
such that 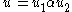 and
and 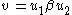 . Thus,
. Thus,  is the result of applying the rule
is the result of applying the rule 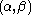 to
to  .
.
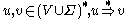 (or
(or 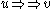 in some textbooks), if
in some textbooks), if 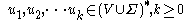 such that
such that 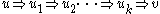
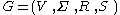 is the set
is the set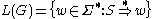
A language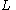 is said to be a context-free language (CFL), if there exists a CFG
is said to be a context-free language (CFL), if there exists a CFG 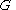 , such that
, such that 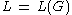 .
.
The grammar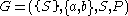 , with productions
, with productions
is context-free. A typical derivation in this grammar is
S → aSa → aaSaa → aabSbaa → aabbaa.
This makes it clear that
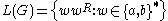 .
.
The language is context-free, however it can be proved that it is not regular.
The first rule allows Ss to multiply; the second rule allows Ss to become enclosed by matching parentheses; and the third rule terminates the recursion.
Starting with S, and applying the rules, one can construct:
with terminal symbols [ ] and nonterminal S.
The following sequence can be derived in that grammar:
However, there is no context-free grammar for generating all sequences of two different types of parentheses, each separately balanced disregarding the other, but where the two types need not nest inside one another, for example:
The terminals here are a and b, while the only non-terminal is S.
The language described is all nonempty strings of s and
s and 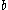 s that end in
s that end in  .
.
This grammar is regular
: no rule has more than one nonterminal in its right-hand side, and each of these nonterminals is at the same end of the right-hand side.
Every regular grammar corresponds directly to a nondeterministic finite automaton, so we know that this is a regular language
.
It is common to list all right-hand sides for the same left-hand side on the same line, using | (the pipe symbol) to separate them. Hence the grammar above can be described more tersely as follows:
s. The simplest example:
This grammar generates the language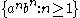 , which is not regular
, which is not regular
(according to the Pumping Lemma
for regular languages).
The special character ε stands for the empty string. By changing the above grammar to
we obtain a grammar generating the language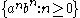 instead. This differs only in that it contains the empty string while the original grammar did not.
instead. This differs only in that it contains the empty string while the original grammar did not.
algebraic expressions in the variables x, y and z:
This grammar can, for example, generate the string
* x - z * y / ( x + x )
as follows:
Note that many choices were made underway as to which rewrite was going to be performed next.
These choices look quite arbitrary. As a matter of fact, they are, in the sense that the string finally generated is always the same. For example, the second and third rewrites
could be done in the opposite order:
Also, many choices were made on which rule to apply to each selected
Changing the choices made and not only the order they were made in usually affects which terminal string comes out at the end.
Let's look at this in more detail. Consider the parse tree
of this derivation:
Starting at the top, step by step, an S in the tree is expanded, until no more unexpanded
Picking a different order of expansion will produce a different derivation, but the same parse tree.
The parse tree will only change if we pick a different rule to apply at some position in the tree.
But can a different parse tree still produce the same terminal string,
which is
Yes, for this particular grammar, this is possible.
Grammars with this property are called ambiguous
.
For example,
However, the language described by this grammar is not inherently ambiguous:
an alternative, unambiguous grammar can be given for the language, for example:
(once again picking
Here, the nonterminal T can generate all strings with the same number of a's as b's, the nonterminal U generates all strings with more a's than b's and the nonterminal V generates all strings with fewer a's than b's.
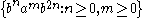 . It is context-free as it can be generated by the following context-free grammar:
. It is context-free as it can be generated by the following context-free grammar:
Context-free grammars are not limited in application to mathematical ("formal") languages.
For example, it has been suggested that a class of Tamil
poetry called Venpa
is described by a context-free grammar.
A derivation proves that the string belongs to the grammar's language.
A derivation is fully determined by giving, for each step:
For clarity, the intermediate string is usually given as well.
For instance, with the grammar:
(1) S → S + S
(2) S → 1
(3) S → a
the string
1 + 1 + a
can be derived with the derivation:
S
→ (rule 1 on first S)
S+S
→ (rule 1 on second S)
S+S+S
→ (rule 2 on second S)
S+1+S
→ (rule 3 on third S)
S+1+a
→ (rule 2 on first S)
1+1+a
Often, a strategy is followed that deterministically determines the next nonterminal to rewrite:
Given such a strategy, a derivation is completely determined by the sequence of rules applied. For instance, the leftmost derivation
S
→ (rule 1 on first S)
S+S
→ (rule 2 on first S)
1+S
→ (rule 1 on first S)
1+S+S
→ (rule 2 on first S)
1+1+S
→ (rule 3 on first S)
1+1+a
can be summarized as
rule 1, rule 2, rule 1, rule 2, rule 3
The distinction between leftmost derivation and rightmost derivation is important because in most parser
s the transformation of the input is defined by giving a piece of code for every grammar rule that is executed whenever the rule is applied. Therefore it is important to know whether the parser determines a leftmost or a rightmost derivation because this determines the order in which the pieces of code will be executed. See for an example LL parser
s and LR parser
s.
A derivation also imposes in some sense a hierarchical structure on the string that is derived. For example, if the string "1 + 1 + a" is derived according to the leftmost derivation:
the structure of the string would be:
where { ... }S indicates a substring recognized as belonging to S. This hierarchy can also be seen as a tree:
This tree is called a concrete syntax tree
(see also abstract syntax tree
) of the string. In this case the presented leftmost and the rightmost derivations define the same syntax tree; however, there is another (rightmost) derivation of the same string
and this defines the following syntax tree:
If, for certain strings in the language of the grammar, there is more than one parsing tree, then the grammar is said to be an ambiguous grammar
. Such grammars are usually hard to parse because the parser cannot always decide which grammar rule it has to apply. Usually, ambiguity is a feature of the grammar, not the language, and an unambiguous grammar can be found that generates the same context-free language. However, there are certain languages that can only be generated by ambiguous grammars; such languages are called inherently ambiguous.
 , but there need be no other ε-rule. Every context-free grammar with no ε-production has an equivalent grammar in Chomsky normal form
, but there need be no other ε-rule. Every context-free grammar with no ε-production has an equivalent grammar in Chomsky normal form
or Greibach normal form
. "Equivalent" here means that the two grammars generate the same language.
Because of the especially simple form of production rules in Chomsky Normal Form grammars, this normal form has both theoretical and practical implications. For instance, given a context-free grammar, one can use the Chomsky Normal Form to construct a polynomial-time algorithm that decides whether a given string is in the language represented by that grammar or not (the CYK algorithm
).
s, but decidable for context-free grammars.
Still, many problems remain undecidable. Examples:
A reduction can be demonstrated to this problem from the well-known undecidable problem of determining whether a Turing machine
accepts a particular input (the Halting problem
). The reduction uses the concept of a computation history
, a string describing an entire computation of a Turing machine
. We can construct a CFG that generates all strings that are not accepting computation histories for a particular Turing machine on a particular input, and thus it will accept all strings only, if the machine doesn't accept that input.
The undecidability of this problem is a direct consequence of the previous: we cannot even decide whether a CFG is equivalent to the trivial CFG defining the language of all strings.
If this problem is decidable, then we could use it to determine whether two CFGs G1 and G2 generate the same language by checking whether L(G1) is a subset of L(G2) and L(G2) is a subset of L(G1).
, does it describe a context-free language?
Given a context-free grammar, does it describe a regular language
?
Each of these problems is undecidable.
and reference
, and programming language analogs such as the correct use and definition of identifiers, to be expressed in a natural way. E.g. we can now easily express that in English sentences, the subject and verb must agree in number.
In computer science, examples of this approach include affix grammar
s, attribute grammar
s, indexed grammar
s, and Van Wijngaarden two-level grammar
s.
Similar extensions exist in linguistics.
Another extension is to allow additional terminal symbols to appear at the left hand side of rules, constraining their application. This produces the formalism of context-sensitive grammar
s.
LR parsing extends LL parsing to support a larger range of grammars; in turn, generalized LR parsing
extends LR parsing to support arbitrary context-free grammars. On LL grammars and LR grammars, it essentially performs LL parsing and LR parsing, respectively, while on nondeterministic grammars, it is as efficient as can be expected. Although GLR parsing was developed in the 1980s, many new language definitions and parser generators continue to be based on LL, LALR or LR parsing up to the present day.
initially hoped to overcome the limitations of context-free grammars by adding transformation rules
.
Such rules are another standard device in traditional linguistics; e.g. passivization in English. Much of generative grammar
has been devoted to finding ways of refining the descriptive mechanisms of phrase-structure grammar and transformation rules such that exactly the kinds of things can be expressed that natural language actually allows. Allowing arbitrary transformations doesn't meet that goal: they are much too powerful, being Turing complete unless significant restrictions are added (e.g. no transformations that introduce and then rewrite symbols in a context-free fashion).
Chomsky's general position regarding the non-context-freeness of natural language has held up since then, although his specific examples regarding the inadequacy of context-free grammars (CFGs) in terms of their weak generative capacity were later disproved.
Gerald Gazdar
and Geoffrey Pullum
have argued that despite a few non-context-free constructions in natural language (such as cross-serial dependencies in Swiss German
and reduplication
in Bambara
), the vast majority of forms in natural language are indeed context-free.
is a formal grammar
Formal grammar
A formal grammar is a set of formation rules for strings in a formal language. The rules describe how to form strings from the language's alphabet that are valid according to the language's syntax...
in which every production rule
Production (computer science)
A production or production rule in computer science is a rewrite rule specifying a symbol substitution that can be recursively performed to generate new symbol sequences. A finite set of productions P is the main component in the specification of a formal grammar...
is of the form
- V → w
where V is a single nonterminal symbol, and w is a string of terminal
Terminal and nonterminal symbols
In computer science, terminal and nonterminal symbols are the lexical elements used in specifying the production rules that constitute a formal grammar...
s and/or nonterminals (w can be empty).
The language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
s generated by context-free grammars are known as the context-free language
Context-free language
In formal language theory, a context-free language is a language generated by some context-free grammar. The set of all context-free languages is identical to the set of languages accepted by pushdown automata.-Examples:...
s.
Context-free grammars are important in linguistics
Linguistics
Linguistics is the scientific study of human language. Linguistics can be broadly broken into three categories or subfields of study: language form, language meaning, and language in context....
for describing the structure of sentences and words in natural language
Natural language
In the philosophy of language, a natural language is any language which arises in an unpremeditated fashion as the result of the innate facility for language possessed by the human intellect. A natural language is typically used for communication, and may be spoken, signed, or written...
, and in computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
for describing the structure of programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s and other artificial languages.
In linguistics
Linguistics
Linguistics is the scientific study of human language. Linguistics can be broadly broken into three categories or subfields of study: language form, language meaning, and language in context....
, some authors use the term phrase structure grammar
Phrase structure grammar
The term phrase structure grammar was originally introduced by Noam Chomsky as the term for grammars as defined by phrase structure rules, i.e. rewrite rules of the type studied previously by Emil Post and Axel Thue...
to refer to context-free grammars, whereby phrase structure grammars are distinct from dependency grammars
Dependency grammar
Dependency grammar is a class of modern syntactic theories that are all based on the dependency relation and that can be traced back primarily to the work of Lucien Tesnière. Dependency grammars are distinct from phrase structure grammars , since they lack phrasal nodes. Structure is determined by...
. In computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a popular notation for context-free grammars is Backus–Naur Form
Backus–Naur form
In computer science, BNF is a notation technique for context-free grammars, often used to describe the syntax of languages used in computing, such as computer programming languages, document formats, instruction sets and communication protocols.It is applied wherever exact descriptions of...
, or BNF.
Background
Since the time of Pāṇini, at least, linguists have described the grammarGrammar
In linguistics, grammar is the set of structural rules that govern the composition of clauses, phrases, and words in any given natural language. The term refers also to the study of such rules, and this field includes morphology, syntax, and phonology, often complemented by phonetics, semantics,...
s of languages in terms of their block structure
Block structure
* In mathematics, block structure is a possible property of matrices - see block matrix.* In computer science, a programming language has block structure if it features blocks which can be nested to any depth....
, and described how sentences are recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
built up from smaller phrases, and eventually individual words or word elements.
An essential property of these block structures is that logical units never overlap. For example, the sentence:
-
- John, whose blue car was in the garage, walked to the green store.
can be logically parenthesized as follows:
-
- (John, ((whose blue car) (was (in the garage)))), (walked (to (the green store))).
A context-free grammar provides a simple and mathematically precise mechanism for describing the methods by which phrases in some natural language are built from smaller blocks, capturing the "block structure" of sentences in a natural way. Its simplicity makes the formalism amenable to rigorous mathematical study. Important features of natural language syntax such as agreement
Agreement (linguistics)
In languages, agreement or concord is a form of cross-reference between different parts of a sentence or phrase. Agreement happens when a word changes form depending on the other words to which it relates....
and reference
Reference
Reference is derived from Middle English referren, from Middle French rèférer, from Latin referre, "to carry back", formed from the prefix re- and ferre, "to bear"...
are not part of the context-free grammar, but the basic recursive structure of sentences, the way in which clauses nest inside other clauses, and the way in which lists of adjectives and adverbs are swallowed by nouns and verbs, is described exactly.
The formalism of context-free grammars was developed in the mid-1950s by Noam Chomsky
Noam Chomsky
Avram Noam Chomsky is an American linguist, philosopher, cognitive scientist, and activist. He is an Institute Professor and Professor in the Department of Linguistics & Philosophy at MIT, where he has worked for over 50 years. Chomsky has been described as the "father of modern linguistics" and...
, and also their classification as a special type
Chomsky hierarchy
Within the field of computer science, specifically in the area of formal languages, the Chomsky hierarchy is a containment hierarchy of classes of formal grammars....
of formal grammar
Formal grammar
A formal grammar is a set of formation rules for strings in a formal language. The rules describe how to form strings from the language's alphabet that are valid according to the language's syntax...
(which he called phrase-structure grammars).
In Chomsky's generative grammar
Generative grammar
In theoretical linguistics, generative grammar refers to a particular approach to the study of syntax. A generative grammar of a language attempts to give a set of rules that will correctly predict which combinations of words will form grammatical sentences...
framework, the syntax of natural language was described by a context-free rules combined with transformation rules.
In later work (e.g. Chomsky 1981), the idea of formulating a grammar consisting of explicit rewrite rules was abandoned. In other generative frameworks, e.g. Generalized Phrase Structure Grammar (Gazdar et al. 1985), context-free grammars were taken to be the mechanism for the entire syntax, eliminating transformations.
Block structure was introduced into computer programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s by the Algol project (1957-1960), which, as a consequence, also featured a context-free grammar to describe the resulting Algol syntax. This became a standard feature of computer languages, and the notation for grammars used in concrete descriptions of computer languages came to be known as Backus-Naur Form, after two members of the Algol language design committee.
The "block structure" aspect that context-free grammars capture is so fundamental to grammar that the terms syntax and grammar are often identified with context-free grammar rules, especially in computer science. Formal constraints not captured by the grammar are then considered to be part of the "semantics" of the language.
Context-free grammars are simple enough to allow the construction of efficient parsing algorithms which, for a given string, determine whether and how it can be generated from the grammar. An Earley parser
Earley parser
In computer science, the Earley parser is an algorithm for parsing strings that belong to a given context-free language, named after its inventor, Jay Earley...
is an example of such an algorithm, while the widely used LR
LR parser
In computer science, an LR parser is a parser that reads input from Left to right and produces a Rightmost derivation. The term LR parser is also used; where the k refers to the number of unconsumed "look ahead" input symbols that are used in making parsing decisions...
and LL parser
LL parser
An LL parser is a top-down parser for a subset of the context-free grammars. It parses the input from Left to right, and constructs a Leftmost derivation of the sentence...
s are simpler algorithms that deal only with more restrictive subsets of context-free grammars.
Formal definitions
A context-free grammar G is defined by the 4-tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
:
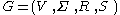
where
1.
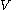 is a finite set; each element
is a finite set; each element 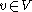 is called a non-terminal character or a variable. Each variable represents a different type of phrase or clause in the sentence. Variables are also sometimes called syntactic categories. Each variable defines a sub-language of the language defined by
is called a non-terminal character or a variable. Each variable represents a different type of phrase or clause in the sentence. Variables are also sometimes called syntactic categories. Each variable defines a sub-language of the language defined by 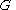 .
.2.
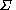 is a finite set of terminals, disjoint from
is a finite set of terminals, disjoint from 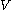 , which make up the actual content of the sentence. The set of terminals is the alphabet of the language defined by the grammar
, which make up the actual content of the sentence. The set of terminals is the alphabet of the language defined by the grammar 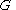 .
.3.
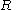 is a finite relation from
is a finite relation from 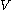 to
to 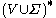 . The members of
. The members of 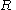 are called the (rewrite) rules or productions of the grammar. (also commonly symbolized by a
are called the (rewrite) rules or productions of the grammar. (also commonly symbolized by a 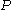 )
)4.
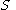 is the start variable (or start symbol), used to represent the whole sentence (or program). It must be an element of
is the start variable (or start symbol), used to represent the whole sentence (or program). It must be an element of 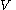 .
.The asterisk represents the Kleene star
Kleene star
In mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
operation.
Rule application
For any strings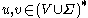 , we say
, we say 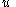 yields
yields 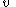 , written as
, written as 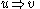 , if
, if 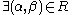 with
with 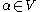 and
and 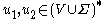 such that
such that 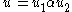 and
and 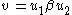 . Thus,
. Thus,  is the result of applying the rule
is the result of applying the rule 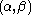 to
to  .
.Repetitive rule application
For any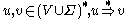 (or
(or 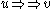 in some textbooks), if
in some textbooks), if 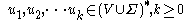 such that
such that 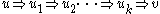
Context-free language
The language of a grammar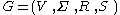 is the set
is the set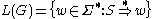
A language
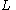 is said to be a context-free language (CFL), if there exists a CFG
is said to be a context-free language (CFL), if there exists a CFG 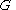 , such that
, such that 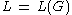 .
.Proper CFGs
A context-free grammar is said to be proper, if it has- no inaccessible symbols:

- no unproductive symbols:

- no ε-productions:
 ε
ε - no cycles:
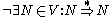
The grammar
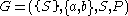 , with productions
, with productions- S → aSa,
- S → bSb,
- S → ε,
is context-free. A typical derivation in this grammar is
S → aSa → aaSaa → aabSbaa → aabbaa.
This makes it clear that
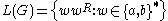 .
.The language is context-free, however it can be proved that it is not regular.
Well-formed parentheses
The canonical example of a context free grammar is parenthesis matching, which is representative of the general case. There are two terminal symbols "(" and ")" and one nonterminal symbol S. The production rules are- S → SS
- S → (S)
- S →
The first rule allows Ss to multiply; the second rule allows Ss to become enclosed by matching parentheses; and the third rule terminates the recursion.
Starting with S, and applying the rules, one can construct:
- S → SS → SSS → (S)SS → ((S))SS → ((SS))S(S)
- → ((S))S(S) → (())S(S) → (())(S)
- → (())()
Well-formed nested parentheses and square brackets
A second canonical example is two different kinds of matching nested parentheses, described by the productions:- S → SS
- S →
- S → (S)
- S → []
- S → [S]
with terminal symbols [ ] and nonterminal S.
The following sequence can be derived in that grammar:
- ([ [ [ [ ][ ] ] ]([ ]) ])
However, there is no context-free grammar for generating all sequences of two different types of parentheses, each separately balanced disregarding the other, but where the two types need not nest inside one another, for example:
- [ [ [ [(((( ] ] ] ]))))(([ ))(([ ))([ )( ])( ])( ])
A regular grammar
- S → a
- S → aS
- S → bS
The terminals here are a and b, while the only non-terminal is S.
The language described is all nonempty strings of
 s and
s and 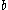 s that end in
s that end in  .
.This grammar is regular
Regular grammar
In theoretical computer science, a regular grammar is a formal grammar that describes a regular language.- Strictly regular grammars :A right regular grammar is a formal grammar such that all the production rules in P are of one of the following forms:# B → a - where B is a non-terminal in N and...
: no rule has more than one nonterminal in its right-hand side, and each of these nonterminals is at the same end of the right-hand side.
Every regular grammar corresponds directly to a nondeterministic finite automaton, so we know that this is a regular language
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
.
It is common to list all right-hand sides for the same left-hand side on the same line, using | (the pipe symbol) to separate them. Hence the grammar above can be described more tersely as follows:
- S → a | aS | bS
Matching pairs
In a context-free grammar, we can pair up characters the way we do with bracketBracket
Brackets are tall punctuation marks used in matched pairs within text, to set apart or interject other text. In the United States, "bracket" usually refers specifically to the "square" or "box" type.-List of types:...
s. The simplest example:
- S → aSb
- S → ab
This grammar generates the language
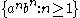 , which is not regular
, which is not regularRegular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
(according to the Pumping Lemma
Pumping lemma
In the theory of formal languages in computability theory, a pumping lemma or pumping argument states that, for a particular language to be a member of a language class, any sufficiently long string in the language contains a section, or sections, that can be removed, or repeated any number of...
for regular languages).
The special character ε stands for the empty string. By changing the above grammar to
- S → aSb | ε
we obtain a grammar generating the language
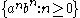 instead. This differs only in that it contains the empty string while the original grammar did not.
instead. This differs only in that it contains the empty string while the original grammar did not.Algebraic expressions
Here is a context-free grammar for syntactically correct infixInfix notation
Infix notation is the common arithmetic and logical formula notation, in which operators are written infix-style between the operands they act on . It is not as simple to parse by computers as prefix notation or postfix notation Infix notation is the common arithmetic and logical formula notation,...
algebraic expressions in the variables x, y and z:
- S → x
- S → y
- S → z
- S → S + S
- S → S - S
- S → S * S
- S → S / S
- S → ( S )
This grammar can, for example, generate the string
* x - z * y / ( x + x )
as follows:
- S (the start symbol)
- → S - S (by rule 5)
- → S * S - S (by rule 6, applied to the leftmost S)
- → S * S - S / S (by rule 7, applied to the rightmost S)
- → ( S ) * S - S / S (by rule 8, applied to the leftmost S)
- → ( S ) * S - S / ( S ) (by rule 8, applied to the rightmost S)
- → ( S + S ) * S - S / ( S ) (etc.)
- → ( S + S ) * S - S * S / ( S )
- → ( S + S ) * S - S * S / ( S + S )
- → ( x + S ) * S - S * S / ( S + S )
- → ( x + y ) * S - S * S / ( S + S )
- → ( x + y ) * x - S * y / ( S + S )
- → ( x + y ) * x - S * y / ( x + S )
- → ( x + y ) * x - z * y / ( x + S )
- → ( x + y ) * x - z * y / ( x + x )
Note that many choices were made underway as to which rewrite was going to be performed next.
These choices look quite arbitrary. As a matter of fact, they are, in the sense that the string finally generated is always the same. For example, the second and third rewrites
- → S * S - S (by rule 6, applied to the leftmost S)
- → S * S - S / S (by rule 7, applied to the rightmost S)
could be done in the opposite order:
- → S - S / S (by rule 7, applied to the rightmost S)
- → S * S - S / S (by rule 6, applied to the leftmost S)
Also, many choices were made on which rule to apply to each selected
S.Changing the choices made and not only the order they were made in usually affects which terminal string comes out at the end.
Let's look at this in more detail. Consider the parse tree
Parse tree
A concrete syntax tree or parse tree or parsing treeis an ordered, rooted tree that represents the syntactic structure of a string according to some formal grammar. In a parse tree, the interior nodes are labeled by non-terminals of the grammar, while the leaf nodes are labeled by terminals of the...
of this derivation:
S
|
/|\
S - S
/ \
/|\ /|\
S * S S / S
/ | | \
/|\ x /|\ /|\
( S ) S * S ( S )
/ | | \
/|\ z y /|\
S + S S + S
| | | |
x y x x
Starting at the top, step by step, an S in the tree is expanded, until no more unexpanded
Ses (non-terminals) remain.Picking a different order of expansion will produce a different derivation, but the same parse tree.
The parse tree will only change if we pick a different rule to apply at some position in the tree.
But can a different parse tree still produce the same terminal string,
which is
( x + y ) * x - z * y / ( x + x ) in this case?Yes, for this particular grammar, this is possible.
Grammars with this property are called ambiguous
Ambiguous grammar
In computer science, a context-free grammar is said to be an ambiguous grammar if there exists a string that can be generated by the grammar in more than one way...
.
For example,
x + y * z can be produced with these two different parse trees:
S S
| |
/|\ /|\
S * S S + S
/ \ / \
/|\ z x /|\
x + y y * z
However, the language described by this grammar is not inherently ambiguous:
an alternative, unambiguous grammar can be given for the language, for example:
- T → x
- T → y
- T → z
- S → S + T
- S → S - T
- S → S * T
- S → S / T
- T → ( S )
- S → T
(once again picking
S as the start symbol).Example 1
A context-free grammar for the language consisting of all strings over {a,b} containing an unequal number of a's and b's:- S → U | V
- U → TaU | TaT
- V → TbV | TbT
- T → aTbT | bTaT | ε
Here, the nonterminal T can generate all strings with the same number of a's as b's, the nonterminal U generates all strings with more a's than b's and the nonterminal V generates all strings with fewer a's than b's.
Example 2
Another example of a non-regular language is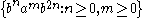 . It is context-free as it can be generated by the following context-free grammar:
. It is context-free as it can be generated by the following context-free grammar:
- S → bSbb | A
- A → aA | ε
Other examples
The formation rules for the terms and formulas of formal logic fit the definition of context-free grammar, except that the set of symbols may be infinite and there may be more than one start symbol.Context-free grammars are not limited in application to mathematical ("formal") languages.
For example, it has been suggested that a class of Tamil
Tamil language
Tamil is a Dravidian language spoken predominantly by Tamil people of the Indian subcontinent. It has official status in the Indian state of Tamil Nadu and in the Indian union territory of Pondicherry. Tamil is also an official language of Sri Lanka and Singapore...
poetry called Venpa
Venpa
Venpa is a form of classical Tamil poetry. Classical Tamil poetry has been classified based upon the rules of metric prosody. Such rules form a context-free grammar. Every Venpa consists of between two to twelve lines....
is described by a context-free grammar.
Derivations and syntax trees
A derivation of a string for a grammar is a sequence of grammar rule applications, that transforms the start symbol into the string.A derivation proves that the string belongs to the grammar's language.
A derivation is fully determined by giving, for each step:
- the rule applied in that step
- the occurrence of its right hand side to which it is applied
For clarity, the intermediate string is usually given as well.
For instance, with the grammar:
(1) S → S + S
(2) S → 1
(3) S → a
the string
1 + 1 + a
can be derived with the derivation:
S
→ (rule 1 on first S)
S+S
→ (rule 1 on second S)
S+S+S
→ (rule 2 on second S)
S+1+S
→ (rule 3 on third S)
S+1+a
→ (rule 2 on first S)
1+1+a
Often, a strategy is followed that deterministically determines the next nonterminal to rewrite:
- in a leftmost derivation, it is always the leftmost nonterminal;
- in a rightmost derivation, it is always the rightmost nonterminal.
Given such a strategy, a derivation is completely determined by the sequence of rules applied. For instance, the leftmost derivation
S
→ (rule 1 on first S)
S+S
→ (rule 2 on first S)
1+S
→ (rule 1 on first S)
1+S+S
→ (rule 2 on first S)
1+1+S
→ (rule 3 on first S)
1+1+a
can be summarized as
rule 1, rule 2, rule 1, rule 2, rule 3
The distinction between leftmost derivation and rightmost derivation is important because in most parser
Parsing
In computer science and linguistics, parsing, or, more formally, syntactic analysis, is the process of analyzing a text, made of a sequence of tokens , to determine its grammatical structure with respect to a given formal grammar...
s the transformation of the input is defined by giving a piece of code for every grammar rule that is executed whenever the rule is applied. Therefore it is important to know whether the parser determines a leftmost or a rightmost derivation because this determines the order in which the pieces of code will be executed. See for an example LL parser
LL parser
An LL parser is a top-down parser for a subset of the context-free grammars. It parses the input from Left to right, and constructs a Leftmost derivation of the sentence...
s and LR parser
LR parser
In computer science, an LR parser is a parser that reads input from Left to right and produces a Rightmost derivation. The term LR parser is also used; where the k refers to the number of unconsumed "look ahead" input symbols that are used in making parsing decisions...
s.
A derivation also imposes in some sense a hierarchical structure on the string that is derived. For example, if the string "1 + 1 + a" is derived according to the leftmost derivation:
- S → S + S (1)
- → 1 + S (2)
- → 1 + S + S (1)
- → 1 + 1 + S (2)
- → 1 + 1 + a (3)
the structure of the string would be:
- { { 1 }S + { { 1 }S + { a }S }S }S
where { ... }S indicates a substring recognized as belonging to S. This hierarchy can also be seen as a tree:
S
/|\
/ | \
/ | \
S '+' S
| /|\
| / | \
'1' S '+' S
| |
'1' 'a'
This tree is called a concrete syntax tree
Parse tree
A concrete syntax tree or parse tree or parsing treeis an ordered, rooted tree that represents the syntactic structure of a string according to some formal grammar. In a parse tree, the interior nodes are labeled by non-terminals of the grammar, while the leaf nodes are labeled by terminals of the...
(see also abstract syntax tree
Abstract syntax tree
In computer science, an abstract syntax tree , or just syntax tree, is a tree representation of the abstract syntactic structure of source code written in a programming language. Each node of the tree denotes a construct occurring in the source code. The syntax is 'abstract' in the sense that it...
) of the string. In this case the presented leftmost and the rightmost derivations define the same syntax tree; however, there is another (rightmost) derivation of the same string
- S → S + S (1)
- → S + a (3)
- → S + S + a (1)
- → S + 1 + a (2)
- → 1 + 1 + a (2)
and this defines the following syntax tree:
S
/|\
/ | \
/ | \
S '+' S
/|\ |
/ | \ |
S '+' S 'a'
| |
'1' '1'
If, for certain strings in the language of the grammar, there is more than one parsing tree, then the grammar is said to be an ambiguous grammar
Ambiguous grammar
In computer science, a context-free grammar is said to be an ambiguous grammar if there exists a string that can be generated by the grammar in more than one way...
. Such grammars are usually hard to parse because the parser cannot always decide which grammar rule it has to apply. Usually, ambiguity is a feature of the grammar, not the language, and an unambiguous grammar can be found that generates the same context-free language. However, there are certain languages that can only be generated by ambiguous grammars; such languages are called inherently ambiguous.
Normal forms
Every context-free grammar that does not generate the empty string can be transformed into one in which no rule has the empty string as a product [a rule with ε as a product is called an ε-production]. If it does generate the empty string, it will be necessary to include the rule , but there need be no other ε-rule. Every context-free grammar with no ε-production has an equivalent grammar in Chomsky normal form
, but there need be no other ε-rule. Every context-free grammar with no ε-production has an equivalent grammar in Chomsky normal formChomsky normal form
In computer science, a context-free grammar is said to be in Chomsky normal form if all of its production rules are of the form:Every grammar in Chomsky normal form is context-free, and conversely, every context-free grammar can be transformed into an equivalent one which is in Chomsky normal form....
or Greibach normal form
Greibach normal form
In computer science and formal language theory, a context-free grammar is in Greibach normal form if the right-hand sides of all productions start with a terminal symbol, optionally followed by some variables. A non-strict form allows one exception to this format restriction for allowing the empty...
. "Equivalent" here means that the two grammars generate the same language.
Because of the especially simple form of production rules in Chomsky Normal Form grammars, this normal form has both theoretical and practical implications. For instance, given a context-free grammar, one can use the Chomsky Normal Form to construct a polynomial-time algorithm that decides whether a given string is in the language represented by that grammar or not (the CYK algorithm
CYK algorithm
The Cocke–Younger–Kasami algorithm is a parsing algorithm for context-free grammars. It employs bottom-up parsing and dynamic programming....
).
Undecidable problems
Some questions that are undecidable for wider classes of grammars become decidable for context-free grammars; e.g. the emptiness problem (whether the grammar generates any terminal strings at all), is undecidable for context-sensitive grammarContext-sensitive grammar
A context-sensitive grammar is a formal grammar in which the left-hand sides and right-hand sides of any production rules may be surrounded by a context of terminal and nonterminal symbols...
s, but decidable for context-free grammars.
Still, many problems remain undecidable. Examples:
Universality
Given a CFG, does it generate the language of all strings over the alphabet of terminal symbols used in its rules?A reduction can be demonstrated to this problem from the well-known undecidable problem of determining whether a Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
accepts a particular input (the Halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
). The reduction uses the concept of a computation history
Computation history
In computer science, a computation history is a sequence of steps taken by an abstract machine in the process of computing its result. Computation histories are frequently used in proofs about the capabilities of certain machines, and particularly about the undecidability of various formal...
, a string describing an entire computation of a Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
. We can construct a CFG that generates all strings that are not accepting computation histories for a particular Turing machine on a particular input, and thus it will accept all strings only, if the machine doesn't accept that input.
Language equality
Given two CFGs, do they generate the same language?The undecidability of this problem is a direct consequence of the previous: we cannot even decide whether a CFG is equivalent to the trivial CFG defining the language of all strings.
Language inclusion
Given two CFGs, can the first generate all strings that the second can generate?If this problem is decidable, then we could use it to determine whether two CFGs G1 and G2 generate the same language by checking whether L(G1) is a subset of L(G2) and L(G2) is a subset of L(G1).
Being in a lower level of the Chomsky hierarchy
Given a context-sensitive grammarContext-sensitive grammar
A context-sensitive grammar is a formal grammar in which the left-hand sides and right-hand sides of any production rules may be surrounded by a context of terminal and nonterminal symbols...
, does it describe a context-free language?
Given a context-free grammar, does it describe a regular language
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
?
Each of these problems is undecidable.
Extensions
An obvious way to extend the context-free grammar formalism is to allow nonterminals to have arguments, the values of which are passed along within the rules. This allows natural language features such as agreementAgreement (linguistics)
In languages, agreement or concord is a form of cross-reference between different parts of a sentence or phrase. Agreement happens when a word changes form depending on the other words to which it relates....
and reference
Reference
Reference is derived from Middle English referren, from Middle French rèférer, from Latin referre, "to carry back", formed from the prefix re- and ferre, "to bear"...
, and programming language analogs such as the correct use and definition of identifiers, to be expressed in a natural way. E.g. we can now easily express that in English sentences, the subject and verb must agree in number.
In computer science, examples of this approach include affix grammar
Affix grammar
An affix grammar is a kind of formal grammar; it is used to describe the syntax of languages, mainly computer languages, using an approach based on how natural language is typically described....
s, attribute grammar
Attribute grammar
An attribute grammar is a formal way to define attributes for the productions of a formal grammar, associating these attributes to values. The evaluation occurs in the nodes of the abstract syntax tree, when the language is processed by some parser or compiler....
s, indexed grammar
Indexed grammar
An indexed grammar is a formal grammar which describes indexed languages. They have three disjoint sets of symbols: the usual terminals and nonterminals, as well as index symbols, which appear only in intermediate derivation steps on a stack associated with the non-terminals of that step.The...
s, and Van Wijngaarden two-level grammar
Two-level grammar
A two-level grammar is a formal grammar that is used to generate another formal grammar , such as one with an infinite rule set . This is how a Van Wijngaarden grammar was used to specify Algol68 . A context free grammar that defines the rules for a second grammar can yield an effectively infinite...
s.
Similar extensions exist in linguistics.
Another extension is to allow additional terminal symbols to appear at the left hand side of rules, constraining their application. This produces the formalism of context-sensitive grammar
Context-sensitive grammar
A context-sensitive grammar is a formal grammar in which the left-hand sides and right-hand sides of any production rules may be surrounded by a context of terminal and nonterminal symbols...
s.
Restrictions
There are a number of important subclasses of the context-free grammars:- LR(k)LR parserIn computer science, an LR parser is a parser that reads input from Left to right and produces a Rightmost derivation. The term LR parser is also used; where the k refers to the number of unconsumed "look ahead" input symbols that are used in making parsing decisions...
grammars (also known as deterministic context-free grammarDeterministic context-free grammarIn formal grammar theory, the deterministic context-free grammars are a proper subset of the context-free grammars. The deterministic context-free grammars are those a deterministic pushdown automaton can recognize...
s) allow parsingParsingIn computer science and linguistics, parsing, or, more formally, syntactic analysis, is the process of analyzing a text, made of a sequence of tokens , to determine its grammatical structure with respect to a given formal grammar...
(string recognition) with deterministic pushdown automataDeterministic pushdown automatonIn automata theory, a pushdown automaton is a finite automaton with an additional stack of symbols; its transitions can take the top symbol on the stack and depend on its value, and they can add new top symbols to the stack....
, but they can only describe deterministic context-free languageDeterministic context-free languageA deterministic context-free language is a formal language which is defined by a deterministic context-free grammar. The set of deterministic context-free languages is called DCFL and is identical to the set of languages accepted by a deterministic pushdown automaton.The set of deterministic...
s.
- Simple LRSLR GrammarIn computer science, an SLR grammar is a class of formal grammar that can be parsed by a simple LR parser.- Definitions :A rule of the form B → y. within a state of a SLR automaton is said to be irreducible or in a reduce state because it has been completely expanded and is incapable of undergoing...
, Look-Ahead LRLALR parserIn computer science, an LALR parser is a type of LR parser based on a finite-state-automata concept. The data structure used by an LALR parser is a pushdown automaton...
grammars are subclasses that allow further simplification of parsing.
- LL(k) and LL(*)LL parserAn LL parser is a top-down parser for a subset of the context-free grammars. It parses the input from Left to right, and constructs a Leftmost derivation of the sentence...
grammars allow parsing by direct construction of a leftmost derivation as described above, and describe even fewer languages.
- Simple grammars are a subclass of the LL(1) grammars mostly interesting for its theoretical property that language equality of simple grammars is decidable, while language inclusion is not.
- Bracketed grammars have the property that the terminal symbols are divided into left and right bracket pairs that always match up in rules.
- Linear grammarLinear grammarIn computer science, a grammar is linear if it is context-free and all of its productions' right hand sides have at most one nonterminal.A linear language is a language generated by some linear grammar.-Example:...
s have no rules with more than one nonterminal in the right hand side.
- Regular grammarRegular grammarIn theoretical computer science, a regular grammar is a formal grammar that describes a regular language.- Strictly regular grammars :A right regular grammar is a formal grammar such that all the production rules in P are of one of the following forms:# B → a - where B is a non-terminal in N and...
s are a subclass of the linear grammars and describe the regularRegular languageIn theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
languages, i.e. they correspond to finite automata and regular expressionRegular expressionIn computing, a regular expression provides a concise and flexible means for "matching" strings of text, such as particular characters, words, or patterns of characters. Abbreviations for "regular expression" include "regex" and "regexp"...
s.
LR parsing extends LL parsing to support a larger range of grammars; in turn, generalized LR parsing
GLR parser
A GLR parser is an extension of an LR parser algorithm to handle nondeterministic and ambiguous grammars. First described in a 1984 paper by Masaru Tomita, it has also been referred to as a "parallel parser"...
extends LR parsing to support arbitrary context-free grammars. On LL grammars and LR grammars, it essentially performs LL parsing and LR parsing, respectively, while on nondeterministic grammars, it is as efficient as can be expected. Although GLR parsing was developed in the 1980s, many new language definitions and parser generators continue to be based on LL, LALR or LR parsing up to the present day.
Linguistic applications
ChomskyNoam Chomsky
Avram Noam Chomsky is an American linguist, philosopher, cognitive scientist, and activist. He is an Institute Professor and Professor in the Department of Linguistics & Philosophy at MIT, where he has worked for over 50 years. Chomsky has been described as the "father of modern linguistics" and...
initially hoped to overcome the limitations of context-free grammars by adding transformation rules
Transformational grammar
In linguistics, a transformational grammar or transformational-generative grammar is a generative grammar, especially of a natural language, that has been developed in the Chomskyan tradition of phrase structure grammars...
.
Such rules are another standard device in traditional linguistics; e.g. passivization in English. Much of generative grammar
Generative grammar
In theoretical linguistics, generative grammar refers to a particular approach to the study of syntax. A generative grammar of a language attempts to give a set of rules that will correctly predict which combinations of words will form grammatical sentences...
has been devoted to finding ways of refining the descriptive mechanisms of phrase-structure grammar and transformation rules such that exactly the kinds of things can be expressed that natural language actually allows. Allowing arbitrary transformations doesn't meet that goal: they are much too powerful, being Turing complete unless significant restrictions are added (e.g. no transformations that introduce and then rewrite symbols in a context-free fashion).
Chomsky's general position regarding the non-context-freeness of natural language has held up since then, although his specific examples regarding the inadequacy of context-free grammars (CFGs) in terms of their weak generative capacity were later disproved.
Gerald Gazdar
Gerald Gazdar
Gerald James Michael Gazdar is a linguist and computer scientist.He was educated at Bradfield College and subsequently graduated from the University of East Anglia with a BA in 1970, and from the University of Reading where he completed his master's degree in 1972 and his PhD in 1976...
and Geoffrey Pullum
Geoffrey Pullum
Geoffrey Keith "Geoff" Pullum is a British-American linguist specialising in the study of English. , he is Professor of General Linguistics at the University of Edinburgh....
have argued that despite a few non-context-free constructions in natural language (such as cross-serial dependencies in Swiss German
Swiss German
Swiss German is any of the Alemannic dialects spoken in Switzerland and in some Alpine communities in Northern Italy. Occasionally, the Alemannic dialects spoken in other countries are grouped together with Swiss German as well, especially the dialects of Liechtenstein and Austrian Vorarlberg...
and reduplication
Reduplication
Reduplication in linguistics is a morphological process in which the root or stem of a word is repeated exactly or with a slight change....
in Bambara
Bambara language
Bambara, more correctly known as Bamanankan , its designation in the language itself , is a language spoken in Mali by as many as six million people...
), the vast majority of forms in natural language are indeed context-free.
See also
- Context-sensitive grammarContext-sensitive grammarA context-sensitive grammar is a formal grammar in which the left-hand sides and right-hand sides of any production rules may be surrounded by a context of terminal and nonterminal symbols...
- Formal grammarFormal grammarA formal grammar is a set of formation rules for strings in a formal language. The rules describe how to form strings from the language's alphabet that are valid according to the language's syntax...
- ParsingParsingIn computer science and linguistics, parsing, or, more formally, syntactic analysis, is the process of analyzing a text, made of a sequence of tokens , to determine its grammatical structure with respect to a given formal grammar...
- Parsing expression grammarParsing expression grammarA parsing expression grammar, or PEG, is a type of analytic formal grammar, i.e. it describes a formal language in terms of a set of rules for recognizing strings in the language...
- Stochastic context-free grammarStochastic context-free grammarA stochastic context-free grammar is a context-free grammar in which each production is augmented with a probability...
- Algorithms for context-free grammar generationContext-free grammar generation algorithmsStraight-line grammars are formal grammars that do not branch nor loop...

