Production (computer science)
Encyclopedia
A production or production rule in computer science is a rewrite rule
specifying a symbol substitution that can be recursively performed to generate new symbol sequences. A finite set of productions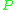
is the main component in the specification of a formal grammar
(specifically a generative grammar
). The other components are a finite set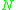
of nonterminal symbols, a finite set (known as an alphabet) 
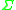of terminal symbols that is disjoint from 
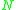and a distinguished symbol 
that is the start symbol.
In an unrestricted grammar
, a production is of the form
where 
and 
are arbitrary strings of terminals and nonterminals however 
may not be the empty string. If 
is the empty string, this is denoted by the symbol 
, or 
(rather than leave the right-hand side blank). So productions are of the form:
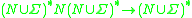
Where
is the Kleene plus operator, 
is the Kleene star
operator, and
denotes set union
.
The other types of formal grammar in the Chomsky hierarchy
impose additional restrictions on what constitutes a production. Notably in a context-free grammar
, the left-hand side of a production must be a single nonterminal symbol. So productions are of the form:
.
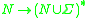
For example, assume the alphabet consists of
and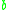 
, with the start symbol 
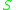, and we have the following rules:
then we start with
, and can choose a rule to apply to it. If we choose rule 1, we replace 
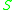with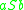 
and obtain the string 
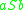. If we choose rule 1 again, we replace 
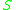with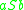 
and obtain the string 
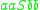. This process is repeated until we only have symbols from the alphabet (i.e., 
and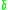 
). If we now choose rule 2, we replace 
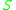with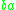 
and obtain the string 
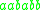, and are done. We can write this series of choices more briefly, using symbols: 
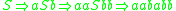. The language of the grammar is the set of all the strings that can be generated using this process: 
.
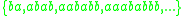Rewrite rule
In linguistics, a rewrite rule for natural language in generative grammar is a rule of the form A → X where A is a syntactic category label, such as noun phrase or sentence, and X is a sequence of such labels and/or morphemes, expressing the fact that A can be replaced by X in generating the...
specifying a symbol substitution that can be recursively performed to generate new symbol sequences. A finite set of productions
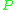is the main component in the specification of a formal grammarFormal grammar
A formal grammar is a set of formation rules for strings in a formal language. The rules describe how to form strings from the language's alphabet that are valid according to the language's syntax...
(specifically a generative grammar
Generative grammar
In theoretical linguistics, generative grammar refers to a particular approach to the study of syntax. A generative grammar of a language attempts to give a set of rules that will correctly predict which combinations of words will form grammatical sentences...
). The other components are a finite set
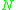of nonterminal symbols, a finite set (known as an alphabet) 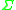of terminal symbols that is disjoint from 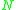and a distinguished symbol that is the start symbol.In an unrestricted grammar
Unrestricted grammar
In formal language theory, an unrestricted grammar is a formal grammar on which no restrictions are made on the left and right sides of the grammar's productions...
, a production is of the form
where and are arbitrary strings of terminals and nonterminals however may not be the empty string. If is the empty string, this is denoted by the symbol , or (rather than leave the right-hand side blank). So productions are of the form: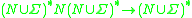Where
is the Kleene plus operator, is the Kleene starKleene star
In mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
operator, and
denotes set unionUnion (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
.
The other types of formal grammar in the Chomsky hierarchy
Chomsky hierarchy
Within the field of computer science, specifically in the area of formal languages, the Chomsky hierarchy is a containment hierarchy of classes of formal grammars....
impose additional restrictions on what constitutes a production. Notably in a context-free grammar
Context-free grammar
In formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
, the left-hand side of a production must be a single nonterminal symbol. So productions are of the form:
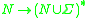
Grammar generation
To generate a string in the language, one begins with a string consisting of only a single start symbol, and then successively applies the rules (any number of times, in any order) to rewrite this string. This stops when we obtain a string containing only terminals. The language consists of all the strings that can be generated in this manner. Any particular sequence of legal choices taken during this rewriting process yields one particular string in the language. If there are multiple different ways of generating this single string, then the grammar is said to be ambiguousAmbiguous grammar
In computer science, a context-free grammar is said to be an ambiguous grammar if there exists a string that can be generated by the grammar in more than one way...
.
For example, assume the alphabet consists of
and 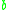, with the start symbol 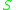, and we have the following rules:- 1.
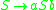
- 2.
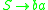
then we start with
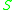, and can choose a rule to apply to it. If we choose rule 1, we replace with 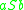and obtain the string 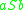. If we choose rule 1 again, we replace 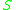with 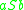and obtain the string 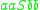. This process is repeated until we only have symbols from the alphabet (i.e., and 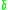). If we now choose rule 2, we replace 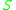with 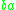and obtain the string 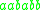, and are done. We can write this series of choices more briefly, using symbols: 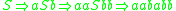. The language of the grammar is the set of all the strings that can be generated using this process: 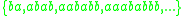.See also
- Formal grammarFormal grammarA formal grammar is a set of formation rules for strings in a formal language. The rules describe how to form strings from the language's alphabet that are valid according to the language's syntax...
- Finite automata
- Generative grammarGenerative grammarIn theoretical linguistics, generative grammar refers to a particular approach to the study of syntax. A generative grammar of a language attempts to give a set of rules that will correctly predict which combinations of words will form grammatical sentences...
- L-systemL-systemAn L-system or Lindenmayer system is a parallel rewriting system, namely a variant of a formal grammar, most famously used to model the growth processes of plant development, but also able to model the morphology of a variety of organisms...
- Rewrite ruleRewrite ruleIn linguistics, a rewrite rule for natural language in generative grammar is a rule of the form A → X where A is a syntactic category label, such as noun phrase or sentence, and X is a sequence of such labels and/or morphemes, expressing the fact that A can be replaced by X in generating the...
- Backus–Naur formBackus–Naur formIn computer science, BNF is a notation technique for context-free grammars, often used to describe the syntax of languages used in computing, such as computer programming languages, document formats, instruction sets and communication protocols.It is applied wherever exact descriptions of...
(A compact form for writing the productions of a context-free grammar.) - Phrase structure rule