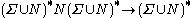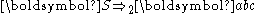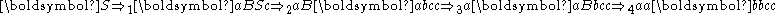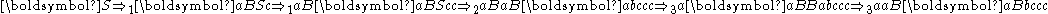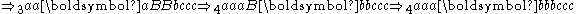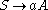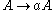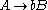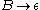Formal grammar
Encyclopedia
A formal grammar is a set of formation rule
s for strings
in a formal language
. The rules describe how to form strings from the language's alphabet that are valid according to the language's syntax. A grammar does not describe the meaning of the strings
or what can be done with them in whatever context—only their form.
Formal language theory, the discipline which studies formal grammars and languages, is a branch of applied mathematics
. Its applications are found in theoretical computer science
, theoretical linguistics
, formal semantics, mathematical logic
, and other areas.
A formal grammar is a set of rules for rewriting strings, along with a "start symbol" from which rewriting must start. Therefore, a grammar is usually thought of as a language generator. However, it can also sometimes be used as the basis for a "recognizer"—a function in computing that determines whether a given string belongs to the language or is grammatically incorrect. To describe such recognizers, formal language theory uses separate formalisms, known as automata theory
. One of the interesting results of automata theory is that it is not possible to design a recognizer for certain formal languages.
Parsing
is the process of recognizing an utterance (a string in natural languages) by breaking it down to a set of symbols and analyzing each one against the grammar of the language. Most languages have the meanings of their utterances structured according to their syntax—a practice known as compositional semantics. As a result, the first step to describing the meaning of an utterance in language is to break it down part by part and look at its analyzed form (known as its parse tree
in computer science, and as its deep structure
in generative grammar
).
.) To generate a string in the language, one begins with a string consisting of only a single start symbol. The production rules are then applied in any order, until a string that contains neither the start symbol nor designated nonterminal symbols is produced. The language formed by the grammar consists of all distinct strings that can be generated in this manner. Any particular sequence of production rules on the start symbol yields a distinct string in the language. If there are multiple ways of generating the same single string, the grammar is said to be ambiguous
.
For example, assume the alphabet consists of a and b, the start symbol is S, and we have the following production rules:
then we start with S, and can choose a rule to apply to it. If we choose rule 1, we obtain the string aSb. If we choose rule 1 again, we replace S with aSb and obtain the string aaSbb. If we now choose rule 2, we replace S with ba and obtain the string aababb, and are done. We can write this series of choices more briefly, using symbols: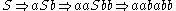
. The language of the grammar is then the infinite set 
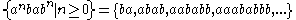, where ak is a repeated k times (and n in particular represents the number of times production rule 1 has been applied).
in the 1950s, a grammar G consists of the following components:
A grammar is formally defined as the tuple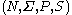
. Such a formal grammar is often called a rewriting system or a phrase structure grammar
in the literature.
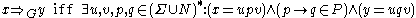
Note that the grammar
is effectively the semi-Thue system
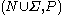, rewriting strings in exactly the same way; the only difference is in that we distinguish specific nonterminal symbols which must be rewritten in rewrite rules, and are only interested in rewritings from the designated start symbol 
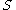to strings without nonterminal symbols.
.
Consider the grammar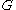
where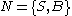 
, 
, 
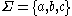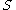is the start symbol, and 
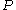consists of the following production rules:
This grammar defines the language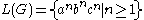
where 
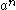denotes a string of n consecutive 
's. Thus, the language is the set of strings that consist of 1 or more 
's, followed by the same number of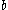 
's, followed by the same number of 
's.
Some examples of the derivation of strings in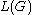
are:
When Noam Chomsky
first formalized generative grammars in 1956, he classified them into types now known as the Chomsky hierarchy
. The difference between these types is that they have increasingly strict production rules and can express fewer formal languages. Two important types are context-free grammar
s (Type 2) and regular grammar
s (Type 3). The languages that can be described with such a grammar are called context-free language
s and regular language
s, respectively. Although much less powerful than unrestricted grammar
s (Type 0), which can in fact express any language that can be accepted by a Turing machine
, these two restricted types of grammars are most often used because parser
s for them can be efficiently implemented. For example, all regular languages can be recognized by a finite state machine
, and for useful subsets of context-free grammars there are well-known algorithms to generate efficient LL parser
s and LR parser
s to recognize the corresponding languages those grammars generate.
is a grammar in which the left-hand side of each production rule consists of only a single nonterminal symbol. This restriction is non-trivial; not all languages can be generated by context-free grammars. Those that can are called context-free languages.
The language defined above is not a context-free language, and this can be strictly proven using the pumping lemma for context-free languages
, but for example the language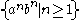
(at least 1 
followed by the same number of 
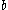's) is context-free, as it can be defined by the grammar 
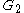with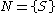 
, 
, 
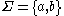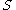the start symbol, and the following production rules:
A context-free language can be recognized in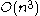
time (see Big O notation
) by an algorithm such as Earley's algorithm. That is, for every context-free language, a machine can be built that takes a string as input and determines in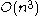
time whether the string is a member of the language, where 
is the length of the string. Further, some important subsets of the context-free languages can be recognized in linear time using other algorithms.
s, the left hand side is again only a single nonterminal symbol, but now the right-hand side is also restricted. The right side may be the empty string, or a single terminal symbol, or a single terminal symbol followed by a nonterminal symbol, but nothing else. (Sometimes a broader definition is used: one can allow longer strings of terminals or single nonterminals without anything else, making languages easier to denote
while still defining the same class of languages.)
The language defined above is not regular, but the language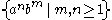
(at least 1 
followed by at least 1 
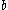, where the numbers may be different) is, as it can be defined by the grammar 
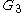with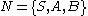 
, 
, 
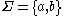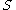the start symbol, and the following production rules:
All languages generated by a regular grammar can be recognized in linear time by a finite state machine
. Although, in practice, regular grammars are commonly expressed using regular expression
s, some forms of regular expression used in practice do not strictly generate the regular languages and do not show linear recognitional performance due to those deviations.
. Some forms of grammars developed include:
algorithms, most of these algorithms assume that the language to be parsed is initially described by means of a generative formal grammar, and that the goal is to transform this generative grammar into a working parser. Strictly speaking, a generative grammar does not in any way correspond to the algorithm used to parse a language, and various algorithms have different restrictions on the form of production rules that are considered well-formed.
An alternative approach is to formalize the language in terms of an analytic grammar in the first place, which more directly corresponds to the structure and semantics of a parser for the language. Examples of analytic grammar formalisms include the following:
Formation rule
In mathematical logic, formation rules are rules for describing which strings of symbols formed from the alphabet of a formal language are syntactically valid within the language. These rules only address the location and manipulation of the strings of the language. It does not describe anything...
s for strings
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
in a formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
. The rules describe how to form strings from the language's alphabet that are valid according to the language's syntax. A grammar does not describe the meaning of the strings
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
or what can be done with them in whatever context—only their form.
Formal language theory, the discipline which studies formal grammars and languages, is a branch of applied mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. Its applications are found in theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
, theoretical linguistics
Theoretical linguistics
Theoretical linguistics is the branch of linguistics that is most concerned with developing models of linguistic knowledge. The fields that are generally considered the core of theoretical linguistics are syntax, phonology, morphology, and semantics...
, formal semantics, mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, and other areas.
A formal grammar is a set of rules for rewriting strings, along with a "start symbol" from which rewriting must start. Therefore, a grammar is usually thought of as a language generator. However, it can also sometimes be used as the basis for a "recognizer"—a function in computing that determines whether a given string belongs to the language or is grammatically incorrect. To describe such recognizers, formal language theory uses separate formalisms, known as automata theory
Automata theory
In theoretical computer science, automata theory is the study of abstract machines and the computational problems that can be solved using these machines. These abstract machines are called automata...
. One of the interesting results of automata theory is that it is not possible to design a recognizer for certain formal languages.
Parsing
Parsing
In computer science and linguistics, parsing, or, more formally, syntactic analysis, is the process of analyzing a text, made of a sequence of tokens , to determine its grammatical structure with respect to a given formal grammar...
is the process of recognizing an utterance (a string in natural languages) by breaking it down to a set of symbols and analyzing each one against the grammar of the language. Most languages have the meanings of their utterances structured according to their syntax—a practice known as compositional semantics. As a result, the first step to describing the meaning of an utterance in language is to break it down part by part and look at its analyzed form (known as its parse tree
Parse tree
A concrete syntax tree or parse tree or parsing treeis an ordered, rooted tree that represents the syntactic structure of a string according to some formal grammar. In a parse tree, the interior nodes are labeled by non-terminals of the grammar, while the leaf nodes are labeled by terminals of the...
in computer science, and as its deep structure
Deep structure
In linguistics, specifically in the study of syntax in the tradition of generative grammar , the deep structure of a linguistic expression is a theoretical construct that seeks to unify several related structures. For example, the sentences "Pat loves Chris" and "Chris is loved by Pat" mean...
in generative grammar
Generative grammar
In theoretical linguistics, generative grammar refers to a particular approach to the study of syntax. A generative grammar of a language attempts to give a set of rules that will correctly predict which combinations of words will form grammatical sentences...
).
Introductory example
A grammar mainly consists of a set of rules for transforming strings. (If it only consisted of these rules, it would be a semi-Thue systemSemi-Thue system
In theoretical computer science and mathematical logic a string rewriting system , historically called a semi-Thue system, is a rewriting system over strings from a alphabet...
.) To generate a string in the language, one begins with a string consisting of only a single start symbol. The production rules are then applied in any order, until a string that contains neither the start symbol nor designated nonterminal symbols is produced. The language formed by the grammar consists of all distinct strings that can be generated in this manner. Any particular sequence of production rules on the start symbol yields a distinct string in the language. If there are multiple ways of generating the same single string, the grammar is said to be ambiguous
Ambiguous grammar
In computer science, a context-free grammar is said to be an ambiguous grammar if there exists a string that can be generated by the grammar in more than one way...
.
For example, assume the alphabet consists of a and b, the start symbol is S, and we have the following production rules:
- 1.
- 2.
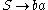
then we start with S, and can choose a rule to apply to it. If we choose rule 1, we obtain the string aSb. If we choose rule 1 again, we replace S with aSb and obtain the string aaSbb. If we now choose rule 2, we replace S with ba and obtain the string aababb, and are done. We can write this series of choices more briefly, using symbols:
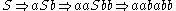. The language of the grammar is then the infinite set 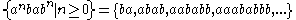, where ak is a repeated k times (and n in particular represents the number of times production rule 1 has been applied).The syntax of grammars
In the classic formalization of generative grammars first proposed by Noam ChomskyNoam Chomsky
Avram Noam Chomsky is an American linguist, philosopher, cognitive scientist, and activist. He is an Institute Professor and Professor in the Department of Linguistics & Philosophy at MIT, where he has worked for over 50 years. Chomsky has been described as the "father of modern linguistics" and...
in the 1950s, a grammar G consists of the following components:
- A finite set N of nonterminal symbols, none of which appear in strings formed from G.
- A finite set
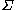of terminal symbols that is disjoint from N. - A finite set P of production rules, each rule of the form
-
-
- where
is the Kleene starKleene starIn mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
operator and
denotes set unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
. That is, each production rule maps from one string of symbols to another, where the first string (the "head") contains an arbitrary number of symbols provided at least one of them is a nonterminal. In the case that the second string (the "body") consists solely of the empty stringEmpty stringIn computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....
– i.e., that it contains no symbols at all – it may be denoted with a special notation (often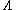
, e or 
) in order to avoid confusion.
- A distinguished symbol
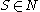that is the start symbol.
- A distinguished symbol
A grammar is formally defined as the tuple
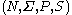. Such a formal grammar is often called a rewriting system or a phrase structure grammarPhrase structure grammar
The term phrase structure grammar was originally introduced by Noam Chomsky as the term for grammars as defined by phrase structure rules, i.e. rewrite rules of the type studied previously by Emil Post and Axel Thue...
in the literature.
The semantics of grammars
The operation of a grammar can be defined in terms of relations on strings:- Given a grammar
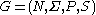, the binary relation 
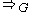on strings in 
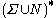is defined by:
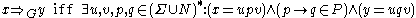
- the relation
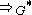is defined as the reflexive transitive closure of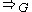 
- a sentential form is a member of
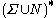that can be derived in a finite number of steps from the start symbol 
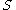; that is, a sentential form is a member of 
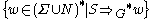. A sentential form that contains no nonterminal symbols (i.e. is a member of 
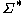) is called a sentence. - the language of
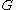, denoted as 
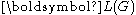, is defined as all those sentences that can be derived in a finite number of steps from the start symbol 
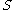; that is, the set 
.
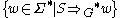Note that the grammar
is effectively the semi-Thue systemSemi-Thue system
In theoretical computer science and mathematical logic a string rewriting system , historically called a semi-Thue system, is a rewriting system over strings from a alphabet...
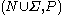, rewriting strings in exactly the same way; the only difference is in that we distinguish specific nonterminal symbols which must be rewritten in rewrite rules, and are only interested in rewritings from the designated start symbol 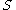to strings without nonterminal symbols.Example
For these examples, formal languages are specified using set-builder notationSet-builder notation
In set theory and its applications to logic, mathematics, and computer science, set-builder notation is a mathematical notation for describing a set by stating the properties that its members must satisfy...
.
Consider the grammar
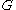where 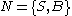, , 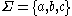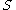is the start symbol, and 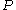consists of the following production rules:- 1.
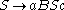
- 2.
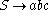
- 3.
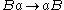
- 4.
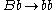
This grammar defines the language
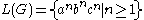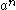where denotes a string of n consecutive 's. Thus, the language is the set of strings that consist of 1 or more 's, followed by the same number of 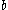's, followed by the same number of 's.Some examples of the derivation of strings in
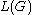are:
The Chomsky hierarchy
When Noam Chomsky
Noam Chomsky
Avram Noam Chomsky is an American linguist, philosopher, cognitive scientist, and activist. He is an Institute Professor and Professor in the Department of Linguistics & Philosophy at MIT, where he has worked for over 50 years. Chomsky has been described as the "father of modern linguistics" and...
first formalized generative grammars in 1956, he classified them into types now known as the Chomsky hierarchy
Chomsky hierarchy
Within the field of computer science, specifically in the area of formal languages, the Chomsky hierarchy is a containment hierarchy of classes of formal grammars....
. The difference between these types is that they have increasingly strict production rules and can express fewer formal languages. Two important types are context-free grammar
Context-free grammar
In formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
s (Type 2) and regular grammar
Regular grammar
In theoretical computer science, a regular grammar is a formal grammar that describes a regular language.- Strictly regular grammars :A right regular grammar is a formal grammar such that all the production rules in P are of one of the following forms:# B → a - where B is a non-terminal in N and...
s (Type 3). The languages that can be described with such a grammar are called context-free language
Context-free language
In formal language theory, a context-free language is a language generated by some context-free grammar. The set of all context-free languages is identical to the set of languages accepted by pushdown automata.-Examples:...
s and regular language
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
s, respectively. Although much less powerful than unrestricted grammar
Unrestricted grammar
In formal language theory, an unrestricted grammar is a formal grammar on which no restrictions are made on the left and right sides of the grammar's productions...
s (Type 0), which can in fact express any language that can be accepted by a Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
, these two restricted types of grammars are most often used because parser
Parsing
In computer science and linguistics, parsing, or, more formally, syntactic analysis, is the process of analyzing a text, made of a sequence of tokens , to determine its grammatical structure with respect to a given formal grammar...
s for them can be efficiently implemented. For example, all regular languages can be recognized by a finite state machine
Finite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
, and for useful subsets of context-free grammars there are well-known algorithms to generate efficient LL parser
LL parser
An LL parser is a top-down parser for a subset of the context-free grammars. It parses the input from Left to right, and constructs a Leftmost derivation of the sentence...
s and LR parser
LR parser
In computer science, an LR parser is a parser that reads input from Left to right and produces a Rightmost derivation. The term LR parser is also used; where the k refers to the number of unconsumed "look ahead" input symbols that are used in making parsing decisions...
s to recognize the corresponding languages those grammars generate.
Context-free grammars
A context-free grammarContext-free grammar
In formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
is a grammar in which the left-hand side of each production rule consists of only a single nonterminal symbol. This restriction is non-trivial; not all languages can be generated by context-free grammars. Those that can are called context-free languages.
The language defined above is not a context-free language, and this can be strictly proven using the pumping lemma for context-free languages
Pumping lemma for context-free languages
The pumping lemma for context-free languages, also known as the Bar-Hillel lemma, is a lemma that gives a property shared by all context-free languages.- Formal statement :...
, but for example the language
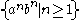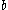(at least 1 followed by the same number of 's) is context-free, as it can be defined by the grammar 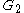with 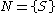, , 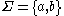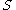the start symbol, and the following production rules:- 1.
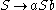
- 2.
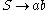
A context-free language can be recognized in
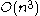time (see Big O notationBig O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
) by an algorithm such as Earley's algorithm. That is, for every context-free language, a machine can be built that takes a string as input and determines in
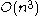time whether the string is a member of the language, where is the length of the string. Further, some important subsets of the context-free languages can be recognized in linear time using other algorithms.Regular grammars
In regular grammarRegular grammar
In theoretical computer science, a regular grammar is a formal grammar that describes a regular language.- Strictly regular grammars :A right regular grammar is a formal grammar such that all the production rules in P are of one of the following forms:# B → a - where B is a non-terminal in N and...
s, the left hand side is again only a single nonterminal symbol, but now the right-hand side is also restricted. The right side may be the empty string, or a single terminal symbol, or a single terminal symbol followed by a nonterminal symbol, but nothing else. (Sometimes a broader definition is used: one can allow longer strings of terminals or single nonterminals without anything else, making languages easier to denote
Syntactic sugar
Syntactic sugar is a computer science term that refers to syntax within a programming language that is designed to make things easier to read or to express....
while still defining the same class of languages.)
The language defined above is not regular, but the language
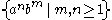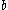(at least 1 followed by at least 1 , where the numbers may be different) is, as it can be defined by the grammar 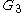with 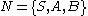, , 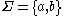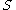the start symbol, and the following production rules:
All languages generated by a regular grammar can be recognized in linear time by a finite state machine
Finite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
. Although, in practice, regular grammars are commonly expressed using regular expression
Regular expression
In computing, a regular expression provides a concise and flexible means for "matching" strings of text, such as particular characters, words, or patterns of characters. Abbreviations for "regular expression" include "regex" and "regexp"...
s, some forms of regular expression used in practice do not strictly generate the regular languages and do not show linear recognitional performance due to those deviations.
Other forms of generative grammars
Many extensions and variations on Chomsky's original hierarchy of formal grammars have been developed, both by linguists and by computer scientists, usually either in order to increase their expressive power or in order to make them easier to analyze or parseParsing
In computer science and linguistics, parsing, or, more formally, syntactic analysis, is the process of analyzing a text, made of a sequence of tokens , to determine its grammatical structure with respect to a given formal grammar...
. Some forms of grammars developed include:
- Tree-adjoining grammarTree-adjoining grammarTree-adjoining grammar is a grammar formalism defined by Aravind Joshi. Tree-adjoining grammars are somewhat similar to context-free grammars, but the elementary unit of rewriting is the tree rather than the symbol...
s increase the expressiveness of conventional generative grammars by allowing rewrite rules to operate on parse treeParse treeA concrete syntax tree or parse tree or parsing treeis an ordered, rooted tree that represents the syntactic structure of a string according to some formal grammar. In a parse tree, the interior nodes are labeled by non-terminals of the grammar, while the leaf nodes are labeled by terminals of the...
s instead of just strings. - Affix grammarAffix grammarAn affix grammar is a kind of formal grammar; it is used to describe the syntax of languages, mainly computer languages, using an approach based on how natural language is typically described....
s and attribute grammarAttribute grammarAn attribute grammar is a formal way to define attributes for the productions of a formal grammar, associating these attributes to values. The evaluation occurs in the nodes of the abstract syntax tree, when the language is processed by some parser or compiler....
s allow rewrite rules to be augmented with semantic attributes and operations, useful both for increasing grammar expressiveness and for constructing practical language translation tools.
Analytic grammars
Though there is a tremendous body of literature on parsingParsing
In computer science and linguistics, parsing, or, more formally, syntactic analysis, is the process of analyzing a text, made of a sequence of tokens , to determine its grammatical structure with respect to a given formal grammar...
algorithms, most of these algorithms assume that the language to be parsed is initially described by means of a generative formal grammar, and that the goal is to transform this generative grammar into a working parser. Strictly speaking, a generative grammar does not in any way correspond to the algorithm used to parse a language, and various algorithms have different restrictions on the form of production rules that are considered well-formed.
An alternative approach is to formalize the language in terms of an analytic grammar in the first place, which more directly corresponds to the structure and semantics of a parser for the language. Examples of analytic grammar formalisms include the following:
- The Language Machine directly implements unrestricted analytic grammars. Substitution rules are used to transform an input to produce outputs and behaviour. The system can also produce the lm-diagram which shows what happens when the rules of an unrestricted analytic grammar are being applied.
- Top-down parsing languageTop-down parsing languageTop-Down Parsing Language is a type of analytic formal grammar developed by Alexander Birman in the early 1970s in order to study formally the behavior of a common class of practical top-down parsers that support a limited form of backtracking...
(TDPL): a highly minimalist analytic grammar formalism developed in the early 1970s to study the behavior of top-down parsersTop-down parsingTop-down parsing is a type of parsing strategy where in one first looks at the highest level of the parse tree and works down the parse tree by using the rewriting rules of a formal grammar...
. - Link grammarLink grammarLink grammar is a theory of syntax by Davy Temperley and Daniel Sleator which builds relations between pairs of words, rather than constructing constituents in a tree-like hierarchy. There are two basic parameters: directionality and distance...
s: a form of analytic grammar designed for linguisticsLinguisticsLinguistics is the scientific study of human language. Linguistics can be broadly broken into three categories or subfields of study: language form, language meaning, and language in context....
, which derives syntactic structure by examining the positional relationships between pairs of words. - Parsing expression grammarParsing expression grammarA parsing expression grammar, or PEG, is a type of analytic formal grammar, i.e. it describes a formal language in terms of a set of rules for recognizing strings in the language...
s (PEGs): a more recent generalization of TDPL designed around the practical expressiveness needs of programming languageProgramming languageA programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
and compilerCompilerA compiler is a computer program that transforms source code written in a programming language into another computer language...
writers.