Semi-Thue system
Encyclopedia
In theoretical computer science
and mathematical logic
a string rewriting system (SRS), historically called a semi-Thue system, is a rewriting
system over strings
from a (usually finite) alphabet. Given a binary relation
R between fixed strings in the alphabet, called rewrite rules, denoted by
, an SRS extends the rewriting relation to all strings in which the left- and right-hand side of the rules appear as substring
s, that is
, where s, t, u, and v are strings.
The notion of a semi-Thue system essentially coincides with the presentation of a monoid. Thus they constitute a natural framework for solving the word problem
for monoids and groups.
An SRS can be defined directly as an abstract rewriting system
. It can also be seen as a restricted kind of a term rewriting system. As a formalism, string rewriting systems are Turing complete. The semi-Thue name comes from the Norwegian mathematician Axel Thue
, who introduced systematic treatment of string rewriting systems in an 1914 paper. Thue introduced this notion hoping to solve the word problem for finitely presented semigroups. It wasn't until 1947 the problem was shown to be undecidable
— this result was obtained independently by Emil Post and A. A. Markov Jr.
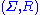where
If the relation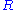
is symmetric
, then the system is called a Thue system.
The rewriting rules on R can be naturally extended to other strings in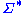
by allowing substrings to be rewritten according to R. More formally, the one-step rewriting relation relation 
induced by R on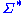 
for any strings s, and t in 
:
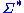Since
is a relation on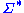 
, the pair 
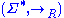fits the definition of an abstract rewriting system
. Obviously R is a subset of
. Some authors use a different notation for the arrow in 
(e.g. 
) in order to distinguish it from R itself (
) because they later want to be able to drop the subscript and still avoid confusion between R and the one-step rewrite induced by R.
Clearly in a semi-Thue system we can form a (finite or infinite) sequence of strings produced by starting with an initial string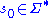
and repeatedly rewriting it by making one substring-replacement at a time:
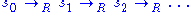
A zero-or-more-steps rewriting like this is captured by the reflexive transitive closure of
, denoted by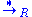 
(see abstract rewriting system#Basic notions). This is called the rewriting relation or reduction relation on 
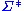induced by R.
of strings on an alphabet forms a free monoid together with the binary operation
of string concatenation (denoted as
and written multiplicatively by dropping the symbol). In a SRS, the reduction relation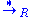 
is compatible with the monoid operation, meaning that 
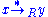implies 
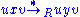for all strings x, y, u, v in 
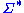. Since 
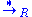is by definition a preorder
,
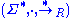forms a preordered monoid.
Similarly, the reflexive transitive symmetric closure of
, denoted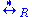 
(see abstract rewriting system#Basic notions), is a congruence
, meaning it is an equivalence relation
(by definition) and it is also compatible with string concatenation. The relation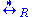
is called the Thue congruence generated by R. In a Thue system, i.e. if R is symmetric, the rewrite relation 
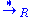coincides with the Thue congruence 
.
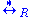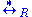is a congruence, we can define the factor monoid 
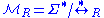of the free monoid 
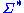by the Thue congruence in the usual manner. If a monoid 
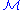is isomorphic with 
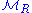, then the semi-Thue system 
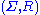is called a monoid presentation of 
.
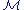We immediately get some very useful connections with other areas of algebra. For example, the alphabet {a, b} with the rules { ab → ε, ba → ε }, where ε is the empty string
, is a presentation of the free group
on one generator. If instead the rules are just { ab → ε }, then we obtain a presentation of the bicyclic monoid.
The importance of semi-Thue systems as presentation of monoids is made stronger by the following:
Theorem: Every monoid has a presentation of the form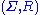
, thus it may be always be presented by a semi-Thue system, possibly over an infinite alphabet.
In this context, the set
is called the set of generators of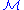 
, and R is called the set of defining relations 
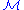. We can immediately classify monoids based on their presentation. 
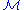is called
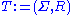and two words 
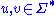, can 
be transformed into 
by applying rules from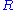 
? This problem is undecidable
, i.e. there is no general algorithm for solving this problem. This even holds if we limit the input to finite systems.
Martin Davis offers the lay reader a two-page proof in his article "What is a Computation?" pp. 258-259 with commentary p. 257. Davis casts the proof in this manner: "Invent [a word problem] whose solution would lead to a solution to the halting problem
."
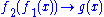is equivalent with the string rule 
.
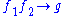A semi-Thue system is also a special type of Post canonical system
, but every Post canonical system can also be reduced to an SRS. Both formalism are Turing complete, and thus equivalent to Noam Chomsky
's unrestricted grammar
s, which are sometimes called semi-Thue grammars. A formal grammar
only differs from a semi-Thue system by the separation of the alphabet in terminals and non-terminals, and the fixation of a starting symbol amongst non-terminals. A minority of authors actually define a semi-Thue system as a triple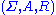
, where 
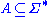is called the set of axioms. Under this "generative" definition of semi-Thue system, an unrestricted grammar is just a semi-Thue system with a single axiom in which one partitions the alphabet in terminals and non-terminals, and makes the axiom a nonterminal. The simple artifice of partitioning the alphabet in terminals and non-terminals is a powerful one; it allows the definition of the Chomsky hierarchy
based on the what combination of terminals and non-terminals rules contain. This was a crucial development in the theory of formal languages.
, so as to create systems such as propositional logic, that would allow general mathematical theorems to be expressed in a formal language
, and then proven and verified in an automatic, mechanical fashion. The hope was that the act of theorem proving could then be reduced to a set of defined manipulations on a set of strings. It was subsequently realized that semi-Thue systems are isomorphic to unrestricted grammar
s, which in turn are known to be isomorphic to Turing machine
s. And although this program of research succeeded in that computers can now be used to verify the proofs of theorems, it also failed in a spectacular way: a computer cannot distinguish between an interesting theorem, and a boring one.
At the suggestion of Alonzo Church
, Emil Post in a paper published in 1947, first proved "a certain Problem of Thue" to be unsolvable, what Martin Davis
states as "...the first unsolvability proof for a problem from classical mathematics -- in this case the word problem for semigroups." (Undecidable p. 292)
Davis [ibid] asserts that the proof was offered independently by A. A. Markov (C. R. (Doklady) Acad. Sci. U.S.S.R. (n.s.) 55(1947), pp. 583-586.
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
and mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
a string rewriting system (SRS), historically called a semi-Thue system, is a rewriting
Rewriting
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a formula with other terms. What is considered are rewriting systems...
system over strings
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
from a (usually finite) alphabet. Given a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
R between fixed strings in the alphabet, called rewrite rules, denoted by
, an SRS extends the rewriting relation to all strings in which the left- and right-hand side of the rules appear as substringSubstring
A subsequence, substring, prefix or suffix of a string is a subset of the symbols in a string, where the order of the elements is preserved...
s, that is
, where s, t, u, and v are strings.The notion of a semi-Thue system essentially coincides with the presentation of a monoid. Thus they constitute a natural framework for solving the word problem
Word problem (mathematics)
In mathematics and computer science, a word problem for a set S with respect to a system of finite encodings of its elements is the algorithmic problem of deciding whether two given representatives represent the same element of the set...
for monoids and groups.
An SRS can be defined directly as an abstract rewriting system
Abstract rewriting system
In mathematical logic and theoretical computer science, an abstract rewriting system is a formalism that captures the quintessential notion and properties of rewriting systems...
. It can also be seen as a restricted kind of a term rewriting system. As a formalism, string rewriting systems are Turing complete. The semi-Thue name comes from the Norwegian mathematician Axel Thue
Axel Thue
Axel Thue was a Norwegian mathematician, known for highly original work in diophantine approximation, and combinatorics....
, who introduced systematic treatment of string rewriting systems in an 1914 paper. Thue introduced this notion hoping to solve the word problem for finitely presented semigroups. It wasn't until 1947 the problem was shown to be undecidable
Undecidable
Undecidable may refer to:In mathematics and logic* Undecidable problem - a decision problem which no algorithm can decide* "Undecidable" is sometimes used as a synonym of "independent", where a formula in mathematical logic is independent of a logical theory if neither that formula nor its negation...
— this result was obtained independently by Emil Post and A. A. Markov Jr.
Andrey Markov (Soviet mathematician)
Andrey Andreyevich Markov Jr. was a Soviet mathematician, the son of the great Russian mathematician Andrey Andreyevich Markov Sr, and one of the key founders of the Russian school of constructive mathematics and logic...
Definition
A string rewriting system or semi-Thue system is a tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
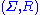where
-
is an alphabet, usually assumed finite. The elements of the set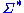 
(* is the Kleene starKleene starIn mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
here) are finite (possibly empty) strings on
, sometimes called words in formal languages; we will simply call them strings here. -
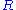is a binary relationBinary relationIn mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
on strings from
, i.e.,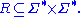 
Each element 
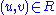is called a (rewriting) rule and is usually written 
.
If the relation
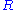is symmetricSymmetric relation
In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
, then the system is called a Thue system.
The rewriting rules on R can be naturally extended to other strings in
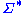by allowing substrings to be rewritten according to R. More formally, the one-step rewriting relation relation induced by R on 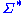for any strings s, and t in :-
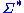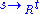if and only if there exist x, y, u, v in 
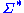such that s = xuy, t = xvy, and 
.
Since
is a relation on 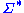, the pair 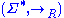fits the definition of an abstract rewriting systemAbstract rewriting system
In mathematical logic and theoretical computer science, an abstract rewriting system is a formalism that captures the quintessential notion and properties of rewriting systems...
. Obviously R is a subset of
. Some authors use a different notation for the arrow in (e.g. ) in order to distinguish it from R itself () because they later want to be able to drop the subscript and still avoid confusion between R and the one-step rewrite induced by R.Clearly in a semi-Thue system we can form a (finite or infinite) sequence of strings produced by starting with an initial string
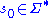and repeatedly rewriting it by making one substring-replacement at a time: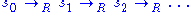A zero-or-more-steps rewriting like this is captured by the reflexive transitive closure of
, denoted by 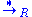(see abstract rewriting system#Basic notions). This is called the rewriting relation or reduction relation on 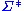induced by R.Thue congruence
In general, the set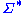 of strings on an alphabet forms a free monoid together with the binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
of string concatenation (denoted as
and written multiplicatively by dropping the symbol). In a SRS, the reduction relation 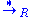is compatible with the monoid operation, meaning that 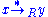implies 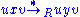for all strings x, y, u, v in 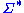. Since 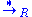is by definition a preorderPreorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
,
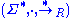forms a preordered monoid.Similarly, the reflexive transitive symmetric closure of
, denoted 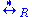(see abstract rewriting system#Basic notions), is a congruenceCongruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
, meaning it is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
(by definition) and it is also compatible with string concatenation. The relation
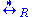is called the Thue congruence generated by R. In a Thue system, i.e. if R is symmetric, the rewrite relation 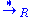coincides with the Thue congruence 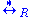.Factor monoid and monoid presentations
Since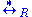 is a congruence, we can define the factor monoid 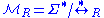of the free monoid 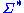by the Thue congruence in the usual manner. If a monoid 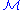is isomorphic with 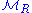, then the semi-Thue system 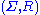is called a monoid presentation of 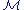.We immediately get some very useful connections with other areas of algebra. For example, the alphabet {a, b} with the rules { ab → ε, ba → ε }, where ε is the empty string
Empty string
In computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....
, is a presentation of the free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
on one generator. If instead the rules are just { ab → ε }, then we obtain a presentation of the bicyclic monoid.
The importance of semi-Thue systems as presentation of monoids is made stronger by the following:
Theorem: Every monoid has a presentation of the form
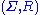, thus it may be always be presented by a semi-Thue system, possibly over an infinite alphabet.In this context, the set
is called the set of generators of 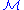, and R is called the set of defining relations 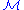. We can immediately classify monoids based on their presentation. 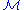is called
- finitely generated if
is finite. - finitely presented if both
and R are finite.
The word problem for semi-Thue systems
The word problem for semi-Thue systems can be stated as follows: Given a semi-Thue system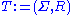 and two words 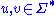, can be transformed into by applying rules from 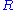? This problem is undecidableUndecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
, i.e. there is no general algorithm for solving this problem. This even holds if we limit the input to finite systems.
Martin Davis offers the lay reader a two-page proof in his article "What is a Computation?" pp. 258-259 with commentary p. 257. Davis casts the proof in this manner: "Invent [a word problem] whose solution would lead to a solution to the halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
."
Connections with other notions
A semi-Thue system is also a term-rewriting system—one that has monadic words (functions) ending in the same variable as left- and right-hand side terms, e.g. a term rule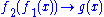 is equivalent with the string rule 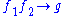.A semi-Thue system is also a special type of Post canonical system
Post canonical system
A Post canonical system, as created by Emil Post, is a string-manipulation system that starts with finitely-many strings and repeatedly transforms them by applying a finite set of specified rules of a certain form, thus generating a formal language...
, but every Post canonical system can also be reduced to an SRS. Both formalism are Turing complete, and thus equivalent to Noam Chomsky
Noam Chomsky
Avram Noam Chomsky is an American linguist, philosopher, cognitive scientist, and activist. He is an Institute Professor and Professor in the Department of Linguistics & Philosophy at MIT, where he has worked for over 50 years. Chomsky has been described as the "father of modern linguistics" and...
's unrestricted grammar
Unrestricted grammar
In formal language theory, an unrestricted grammar is a formal grammar on which no restrictions are made on the left and right sides of the grammar's productions...
s, which are sometimes called semi-Thue grammars. A formal grammar
Formal grammar
A formal grammar is a set of formation rules for strings in a formal language. The rules describe how to form strings from the language's alphabet that are valid according to the language's syntax...
only differs from a semi-Thue system by the separation of the alphabet in terminals and non-terminals, and the fixation of a starting symbol amongst non-terminals. A minority of authors actually define a semi-Thue system as a triple
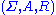, where 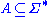is called the set of axioms. Under this "generative" definition of semi-Thue system, an unrestricted grammar is just a semi-Thue system with a single axiom in which one partitions the alphabet in terminals and non-terminals, and makes the axiom a nonterminal. The simple artifice of partitioning the alphabet in terminals and non-terminals is a powerful one; it allows the definition of the Chomsky hierarchyChomsky hierarchy
Within the field of computer science, specifically in the area of formal languages, the Chomsky hierarchy is a containment hierarchy of classes of formal grammars....
based on the what combination of terminals and non-terminals rules contain. This was a crucial development in the theory of formal languages.
History and importance
Semi-Thue systems were developed as part of a program to add additional constructs to logicLogic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, so as to create systems such as propositional logic, that would allow general mathematical theorems to be expressed in a formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
, and then proven and verified in an automatic, mechanical fashion. The hope was that the act of theorem proving could then be reduced to a set of defined manipulations on a set of strings. It was subsequently realized that semi-Thue systems are isomorphic to unrestricted grammar
Unrestricted grammar
In formal language theory, an unrestricted grammar is a formal grammar on which no restrictions are made on the left and right sides of the grammar's productions...
s, which in turn are known to be isomorphic to Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
s. And although this program of research succeeded in that computers can now be used to verify the proofs of theorems, it also failed in a spectacular way: a computer cannot distinguish between an interesting theorem, and a boring one.
At the suggestion of Alonzo Church
Alonzo Church
Alonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
, Emil Post in a paper published in 1947, first proved "a certain Problem of Thue" to be unsolvable, what Martin Davis
Martin Davis
Martin David Davis, is an American mathematician, known for his work on Hilbert's tenth problem . He received his Ph.D. from Princeton University in 1950, where his adviser was Alonzo Church . He is Professor Emeritus at New York University. He is the co-inventor of the Davis-Putnam and the DPLL...
states as "...the first unsolvability proof for a problem from classical mathematics -- in this case the word problem for semigroups." (Undecidable p. 292)
Davis [ibid] asserts that the proof was offered independently by A. A. Markov (C. R. (Doklady) Acad. Sci. U.S.S.R. (n.s.) 55(1947), pp. 583-586.
Monographs
- Ronald V. BookRonald V. BookRonald Vernon Book worked in theoretical computer science. He published more than 150 papers in scientific journals...
and Friedrich Otto, String-rewriting Systems, Springer, 1993, ISBN 0-387-97965-4. - Matthias Jantzen, Confluent string rewriting, Birkhäuser, 1988, ISBN 0-387-13715-7.
Textbooks
- Martin DavisMartin DavisMartin David Davis, is an American mathematician, known for his work on Hilbert's tenth problem . He received his Ph.D. from Princeton University in 1950, where his adviser was Alonzo Church . He is Professor Emeritus at New York University. He is the co-inventor of the Davis-Putnam and the DPLL...
, Ron Sigal, Elaine J. Weyuker, Computability, complexity, and languages: fundamentals of theoretical computer science, 2nd ed., Academic Press, 1994, ISBN 0-12-206382-1, chapter 7 - Elaine Rich, Automata, computability and complexity: theory and applications, Prentice Hall, 2007, ISBN 0-13-228806-0, chapter 23.5.
Surveys
- Samson Abramsky, Dov M. Gabbay, Thomas S. E. Maibaum (ed.), Handbook of Logic in Computer Science: Semantic modelling, Oxford University Press, 1995, ISBN 0-19-853780-8.
- Grzegorz Rozenberg, Arto Salomaa (ed.), Handbook of Formal Languages: Word, language, grammar, Springer, 1997, ISBN 3-540-60420-0.
Landmark papers
- Emil Post (1947), Recursive Unsolvability of a Problem of Thue, The Journal of Symbolic Logic, vol. 12 (1947) pp. 1-11. Reprinted in Martin DavisMartin DavisMartin David Davis, is an American mathematician, known for his work on Hilbert's tenth problem . He received his Ph.D. from Princeton University in 1950, where his adviser was Alonzo Church . He is Professor Emeritus at New York University. He is the co-inventor of the Davis-Putnam and the DPLL...
ed. (1965), The Undecidable: Basic Papers on Undecidable Propositions, Unsolvable Problems and Computable Functions, Raven Press, New York. pp. 293ff