
Preorder
Encyclopedia
In mathematics
, especially in order theory
, preorders are binary relation
s that are reflexive
and transitive
.
For example, all partial orders and equivalence relation
s are preorders. The name quasi-order is also common for preorders.
Many order theoretical definitions for partially ordered sets can be generalized to preorders, but the extra effort of generalization is rarely needed.
≤ on P. Then ≤ is a preorder, or quasiorder, if it is reflexive
and transitive
, i.e., for all a, b and c in P, we have that:
Note that an alternate definition of preorder requires the relation to be irreflexive. However, as this article is examining preorders as a logical extension of partial orders, the current definition is more intuitive.
A set that is equipped with a preorder is called a preordered set.
If a preorder is also antisymmetric
, that is, a ≤ b and b ≤ a implies a = b, then it is a partial order
.
On the other hand, if it is symmetric
, that is, if a ≤ b implies b ≤ a, then it is an equivalence relation
.
A preorder which is preserved in all contexts (i.e. respected by all functions on P) is called a precongruence.
A precongruence which is also symmetric
(i.e. is an equivalence relation
) is a congruence relation
.
Equivalently, a preorder on the set P can be defined as a category
with object set P where every homset has at most one element (one for objects which are related, zero otherwise).
In computer science, one can find examples of the following preorders.
Example of a total preorder:
and reflexive closure, R+=. The transitive closure indicates path connection in R: x R+ y if and only if there is an R-path
from x to y.
Given a preorder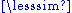 on S one may define an equivalence relation
on S one may define an equivalence relation
~ on S such that a ~ b if and only if a b and b
b and b  a. (The resulting relation is reflexive since a preorder is reflexive, transitive by applying transitivity of the preorder twice, and symmetric by definition.)
a. (The resulting relation is reflexive since a preorder is reflexive, transitive by applying transitivity of the preorder twice, and symmetric by definition.)
Using this relation, it is possible to construct a partial order on the quotient set of the equivalence, S / ~, the set of all equivalence classes of ~. Note that if the preorder is R+=, S / ~ is the set of R-cycle
equivalence classes: x ∈ [y] if and only if x = y or x is in an R-cycle with y. In any case, on S / ~ we can define [x] ≤ [y] if and only if x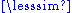 y. By the construction of ~ , this definition is independent of the chosen representatives and the corresponding relation is indeed well-defined. It is readily verified that this yields a partially ordered set.
y. By the construction of ~ , this definition is independent of the chosen representatives and the corresponding relation is indeed well-defined. It is readily verified that this yields a partially ordered set.
Conversely, from a partial order on a partition of a set S one can construct a preorder on S. There is a 1-to-1 correspondence between preorders and pairs (partition, partial order).
For a preorder " ", a relation "<" can be defined as a < b if and only if (a
", a relation "<" can be defined as a < b if and only if (a 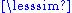 b and not b
b and not b 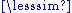 a), or equivalently, using the equivalence relation introduced above, (a
a), or equivalently, using the equivalence relation introduced above, (a  b and not a ~ b). It is a strict partial order; every strict partial order can be the result of such a construction. If the preorder is anti-symmetric, hence a partial order "≤", the equivalence is equality, so the relation "<" can also be defined as a < b if and only if (a ≤ b and a ≠ b).
b and not a ~ b). It is a strict partial order; every strict partial order can be the result of such a construction. If the preorder is anti-symmetric, hence a partial order "≤", the equivalence is equality, so the relation "<" can also be defined as a < b if and only if (a ≤ b and a ≠ b).
(Alternatively, for a preorder " ", a relation "<" can be defined as a < b if and only if (a
", a relation "<" can be defined as a < b if and only if (a 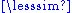 b and a ≠ b). The result is the reflexive reduction of the preorder. However, if the preorder is not anti-symmetric the result is not transitive, and if it is, as we have seen, it is the same as before.)
b and a ≠ b). The result is the reflexive reduction of the preorder. However, if the preorder is not anti-symmetric the result is not transitive, and if it is, as we have seen, it is the same as before.)
Conversely we have a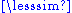 b if and only if a < b or a ~ b. This is the reason for using the notation "
b if and only if a < b or a ~ b. This is the reason for using the notation " "; "≤" can be confusing for a preorder that is not anti-symmetric, it may suggest that a ≤ b implies that a < b or a = b.
"; "≤" can be confusing for a preorder that is not anti-symmetric, it may suggest that a ≤ b implies that a < b or a = b.
Note that with this construction multiple preorders " " can give the same relation "<", so without more information, such as the equivalence relation, "
" can give the same relation "<", so without more information, such as the equivalence relation, "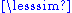 " cannot be reconstructed from "<". Possible preorders include the following:
" cannot be reconstructed from "<". Possible preorders include the following:
 b, the interval
b, the interval
[a,b] is the set of points x satisfying a x and x
x and x 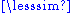 b, also written a
b, also written a  x
x  b. It contains at least the points a and b. One may choose to extend the definition to all pairs (a,b). The extra intervals are all empty.
b. It contains at least the points a and b. One may choose to extend the definition to all pairs (a,b). The extra intervals are all empty.
Using the corresponding strict relation "<", one can also define the interval (a,b) as the set of points x satisfying a < x and x < b, also written a < x < b. An open interval may be empty even if a < b.
Also [a,b) and (a,b] can be defined similarly.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, preorders are binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
s that are reflexive
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
and transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
.
For example, all partial orders and equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
s are preorders. The name quasi-order is also common for preorders.
Many order theoretical definitions for partially ordered sets can be generalized to preorders, but the extra effort of generalization is rarely needed.
Formal definition
Consider some set P and a binary relationBinary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
≤ on P. Then ≤ is a preorder, or quasiorder, if it is reflexive
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
and transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
, i.e., for all a, b and c in P, we have that:
- a ≤ a (reflexivity)
- if a ≤ b and b ≤ c then a ≤ c (transitivity)
Note that an alternate definition of preorder requires the relation to be irreflexive. However, as this article is examining preorders as a logical extension of partial orders, the current definition is more intuitive.
A set that is equipped with a preorder is called a preordered set.
If a preorder is also antisymmetric
Antisymmetric relation
In mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,...
, that is, a ≤ b and b ≤ a implies a = b, then it is a partial order
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
.
On the other hand, if it is symmetric
Symmetric relation
In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
, that is, if a ≤ b implies b ≤ a, then it is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
.
A preorder which is preserved in all contexts (i.e. respected by all functions on P) is called a precongruence.
A precongruence which is also symmetric
Symmetric relation
In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
(i.e. is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
) is a congruence relation
Congruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
.
Equivalently, a preorder on the set P can be defined as a category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
with object set P where every homset has at most one element (one for objects which are related, zero otherwise).
Examples of preorders
- Any collection of sets is preordered by their comparative sizes. Thus {3, 7} ≤ {April, June, July}. This applies equally to infinite sets; as one example, Cantor'sGeorg CantorGeorg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
famous diagonalizationCantor's diagonal argumentCantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor as a mathematical proof that there are infinite sets which cannot be put into one-to-one correspondence with the infinite set of natural...
result that the real numbers are uncountableUncountable setIn mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...
(i.e., more numerous than the integers) may be expressed in terms of this preorder as Z < R. - Logical implication over sentences.
- Every finite topological spaceFinite topological spaceIn mathematics, a finite topological space is a topological space for which the underlying point set is finite. That is, it is a topological space for which there are only finitely many points....
gives rise to a preorder on its points, in which x ≤ y if and only if x belongs to every neighborhood of y, and every finite preorder can be formed as the specialization preorder of a topological space in this way. That is, there is a 1-to-1 correspondenceBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between finite topologies and finite preorders. However, the relation between infinite topological spaces and their specialization preorders is not 1-to-1. - A netNet (mathematics)In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
is a directedDirected setIn mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
preorder, that is, each pair of elements has an upper bound. The definition of convergence via nets is important in topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, where preorders cannot be replaced by partially ordered setPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
s without losing important features. - The relation defined by
 iffIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
iffIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
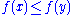 , where f is a function into some preorder.
, where f is a function into some preorder. - The relation defined by
 iffIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
iffIFFIFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
there exists some injectionInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
from x to y. Injection may be replaced by surjection, or any type of structure-preserving function, such as ring homomorphismRing homomorphismIn ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
, or permutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
. - The embeddingEmbeddingIn mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
relation for countable total orderTotal orderIn set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
ings. - The graph-minor relation in graph theoryGraph theoryIn mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
.
In computer science, one can find examples of the following preorders.
- The subtypingSubtypeIn programming language theory, subtyping or subtype polymorphism is a form of type polymorphism in which a subtype is a datatype that is related to another datatype by some notion of substitutability, meaning that program constructs, typically subroutines or functions, written to operate on...
relations are usually preorders. - Simulation preorderSimulation preorderIn theoretical computer science a simulation preorder is a relation between state transition systems associating systems which behave in the same way in the sense that one system simulates the other....
s are preorders (hence the name).
Example of a total preorder:
- PreferencePreference-Definitions in different disciplines:The term “preferences” is used in a variety of related, but not identical, ways in the scientific literature. This makes it necessary to make explicit the sense in which the term is used in different social sciences....
, according to common models.
Constructions
Every binary relation R on a set S can be extended to a preorder on S by taking the transitive closureTransitive closure
In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
and reflexive closure, R+=. The transitive closure indicates path connection in R: x R+ y if and only if there is an R-path
Path (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
from x to y.
Given a preorder
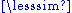 on S one may define an equivalence relation
on S one may define an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
~ on S such that a ~ b if and only if a
 b and b
b and b  a. (The resulting relation is reflexive since a preorder is reflexive, transitive by applying transitivity of the preorder twice, and symmetric by definition.)
a. (The resulting relation is reflexive since a preorder is reflexive, transitive by applying transitivity of the preorder twice, and symmetric by definition.)Using this relation, it is possible to construct a partial order on the quotient set of the equivalence, S / ~, the set of all equivalence classes of ~. Note that if the preorder is R+=, S / ~ is the set of R-cycle
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
equivalence classes: x ∈ [y] if and only if x = y or x is in an R-cycle with y. In any case, on S / ~ we can define [x] ≤ [y] if and only if x
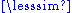 y. By the construction of ~ , this definition is independent of the chosen representatives and the corresponding relation is indeed well-defined. It is readily verified that this yields a partially ordered set.
y. By the construction of ~ , this definition is independent of the chosen representatives and the corresponding relation is indeed well-defined. It is readily verified that this yields a partially ordered set.Conversely, from a partial order on a partition of a set S one can construct a preorder on S. There is a 1-to-1 correspondence between preorders and pairs (partition, partial order).
For a preorder "
 ", a relation "<" can be defined as a < b if and only if (a
", a relation "<" can be defined as a < b if and only if (a 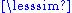 b and not b
b and not b 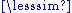 a), or equivalently, using the equivalence relation introduced above, (a
a), or equivalently, using the equivalence relation introduced above, (a  b and not a ~ b). It is a strict partial order; every strict partial order can be the result of such a construction. If the preorder is anti-symmetric, hence a partial order "≤", the equivalence is equality, so the relation "<" can also be defined as a < b if and only if (a ≤ b and a ≠ b).
b and not a ~ b). It is a strict partial order; every strict partial order can be the result of such a construction. If the preorder is anti-symmetric, hence a partial order "≤", the equivalence is equality, so the relation "<" can also be defined as a < b if and only if (a ≤ b and a ≠ b).(Alternatively, for a preorder "
 ", a relation "<" can be defined as a < b if and only if (a
", a relation "<" can be defined as a < b if and only if (a 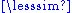 b and a ≠ b). The result is the reflexive reduction of the preorder. However, if the preorder is not anti-symmetric the result is not transitive, and if it is, as we have seen, it is the same as before.)
b and a ≠ b). The result is the reflexive reduction of the preorder. However, if the preorder is not anti-symmetric the result is not transitive, and if it is, as we have seen, it is the same as before.)Conversely we have a
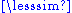 b if and only if a < b or a ~ b. This is the reason for using the notation "
b if and only if a < b or a ~ b. This is the reason for using the notation " "; "≤" can be confusing for a preorder that is not anti-symmetric, it may suggest that a ≤ b implies that a < b or a = b.
"; "≤" can be confusing for a preorder that is not anti-symmetric, it may suggest that a ≤ b implies that a < b or a = b.Note that with this construction multiple preorders "
 " can give the same relation "<", so without more information, such as the equivalence relation, "
" can give the same relation "<", so without more information, such as the equivalence relation, "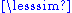 " cannot be reconstructed from "<". Possible preorders include the following:
" cannot be reconstructed from "<". Possible preorders include the following:
- Define a ≤ b as a < b or a = b (i.e., take the reflexive closure of the relation). This gives the partial order associated with the strict partial order "<" through reflexive closure; in this case the equivalence is equality, so we don't need the notations
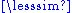 and ~.
and ~. - Define a
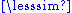 b as "not b < a" (i.e., take the inverse complement of the relation), which corresponds to defining a ~ b as "neither a < b nor b < a"; these relations
b as "not b < a" (i.e., take the inverse complement of the relation), which corresponds to defining a ~ b as "neither a < b nor b < a"; these relations 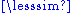 and ~ are in general not transitive; however, if they are, ~ is an equivalence; in that case "<" is a strict weak order. The resulting preorder is totalTotal relationIn mathematics, a binary relation R over a set X is total if for all a and b in X, a is related to b or b is related to a .In mathematical notation, this is\forall a, b \in X,\ a R b \or b R a....
and ~ are in general not transitive; however, if they are, ~ is an equivalence; in that case "<" is a strict weak order. The resulting preorder is totalTotal relationIn mathematics, a binary relation R over a set X is total if for all a and b in X, a is related to b or b is related to a .In mathematical notation, this is\forall a, b \in X,\ a R b \or b R a....
.
Number of preorders
As explained above, there is a 1-to-1 correspondence between preorders and pairs (partition, partial order). Thus the number of preorders is the sum of the number of partial orders on every partition. For example:- for n=3:
- 1 partition of 3, giving 1 preorder
- 3 partitions of 2+1, giving 3 × 3 = 9 preorders
- 1 partition of 1+1+1, giving 19 preorders
- i.e. together 29 preorders.
- for n=4:
- 1 partition of 4, giving 1 preorder
- 7 partitions with two classes (4 of 3+1 and 3 of 2+2), giving 7 × 3 = 21 preorders
- 6 partitions of 2+1+1, giving 6 × 19 = 114 preorders
- 1 partition of 1+1+1+1, giving 219 preorders
- for n=4:
- i.e. together 355 preorders.
Interval
For a b, the interval
b, the intervalInterval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[a,b] is the set of points x satisfying a
 x and x
x and x 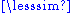 b, also written a
b, also written a  x
x  b. It contains at least the points a and b. One may choose to extend the definition to all pairs (a,b). The extra intervals are all empty.
b. It contains at least the points a and b. One may choose to extend the definition to all pairs (a,b). The extra intervals are all empty.Using the corresponding strict relation "<", one can also define the interval (a,b) as the set of points x satisfying a < x and x < b, also written a < x < b. An open interval may be empty even if a < b.
Also [a,b) and (a,b] can be defined similarly.
See also
- partial orderPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
- preorder that is antisymmetricAntisymmetric relationIn mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,... - equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
- preorder that is symmetricSymmetric relationIn mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:... - total preorder - preorder that is totalTotal relationIn mathematics, a binary relation R over a set X is total if for all a and b in X, a is related to b or b is related to a .In mathematical notation, this is\forall a, b \in X,\ a R b \or b R a....
- total orderTotal orderIn set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
- preorder that is antisymmetric and total - directed setDirected setIn mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
- category of preordered setsCategory of preordered setsThe category Ord has preordered sets as objects and monotonic functions as morphisms. This is a category because the composition of two monotonic functions is monotonic and the identity map is monotonic....
- prewellorderingPrewellorderingIn set theory, a prewellordering is a binary relation that is transitive, wellfounded, and total. In other words, if \leq is a prewellordering on a set X, and if we define \sim byx\sim y\iff x\leq y \land y\leq x...
- preordered classPreordered classIn mathematics, a preordered class is a class equipped with a preorder.-Definition:When dealing with a class C, it is possible to define a class relation on C as a subclass of the power class C \times C . Then, it is convenient to use the language of relations on a set.A preordered class is a...
- Well-quasi-orderingWell-quasi-orderingIn mathematics, specifically order theory, a well-quasi-ordering or wqo is a well-founded quasi-ordering with an additional restriction on sequences - that there is no infinite sequence x_i with x_i \not \le x_j for all i...

