
Transitive relation
Encyclopedia
In mathematics
, a binary relation
R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c.
In mathematical syntax: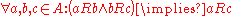
Transitivity is a key property of both partial order relations and equivalence relation
s.
On the other hand, "is the mother of" is not a transitive relation, because if Alice is the mother of Brenda, and Brenda is the mother of Claire, then Alice is not the mother of Claire. What is more, it is antitransitive: Alice can never be the mother of Claire.
Then again, in biology we often need to consider motherhood over an arbitrary number of generations: the relation "is a matrilinear ancestor of". This is a transitive relation. More precisely, it is the transitive closure
of the relation "is the mother of".
More examples of transitive relations:
of" is transitive and "is a superset
of" is its converse, we can conclude that the latter is transitive as well.
The intersection of two transitive relations is always transitive: knowing that "was born before" and "has the same first name as" are transitive, we can conclude that "was born before and also has the same first name as" is also transitive.
The union of two transitive relations is not always transitive. For instance "was born before or has the same first name as" is not generally a transitive relation.
The complement of a transitive relation is not always transitive. For instance, while "equal to" is transitive, "not equal to" is only transitive on sets with at most one element.
s – , those that are symmetric and transitive, those that are symmetric, transitive, and antisymmetric, and those that are total, transitive, and antisymmetric. Pfeiffer has made some progress in this direction, expressing relations with combinations of these properties in terms of each other, but still calculating any one is difficult. See also.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c.
In mathematical syntax:
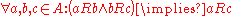
Transitivity is a key property of both partial order relations and equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
s.
Examples
For example, "is greater than," "is at least as great as," and "is equal to" (equality) are transitive relations:- whenever A > B and B > C, then also A > C
- whenever A ≥ B and B ≥ C, then also A ≥ C
- whenever A = B and B = C, then also A = C.
On the other hand, "is the mother of" is not a transitive relation, because if Alice is the mother of Brenda, and Brenda is the mother of Claire, then Alice is not the mother of Claire. What is more, it is antitransitive: Alice can never be the mother of Claire.
Then again, in biology we often need to consider motherhood over an arbitrary number of generations: the relation "is a matrilinear ancestor of". This is a transitive relation. More precisely, it is the transitive closure
Transitive closure
In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
of the relation "is the mother of".
More examples of transitive relations:
- "is a subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of" (set inclusion) - "divides" (divisibilityDivisorIn mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
) - "implies" (implication)
Closure properties
The converse of a transitive relation is always transitive: e.g. knowing that "is a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of" is transitive and "is a superset
SuperSet
SuperSet Software was a group founded by friends and former Eyring Research Institute co-workers Drew Major, Dale Neibaur, Kyle Powell and later joined by Mark Hurst...
of" is its converse, we can conclude that the latter is transitive as well.
The intersection of two transitive relations is always transitive: knowing that "was born before" and "has the same first name as" are transitive, we can conclude that "was born before and also has the same first name as" is also transitive.
The union of two transitive relations is not always transitive. For instance "was born before or has the same first name as" is not generally a transitive relation.
The complement of a transitive relation is not always transitive. For instance, while "equal to" is transitive, "not equal to" is only transitive on sets with at most one element.
Other properties that require transitivity
- PreorderPreorderIn mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
– a reflexiveReflexive relationIn mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
transitive relation - partial orderPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
– an antisymmetricAntisymmetric relationIn mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,...
preorder - Total preorder – a totalTotal relationIn mathematics, a binary relation R over a set X is total if for all a and b in X, a is related to b or b is related to a .In mathematical notation, this is\forall a, b \in X,\ a R b \or b R a....
preorder - Equivalence relationEquivalence relationIn mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
– a symmetricSymmetric relationIn mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
preorder - Strict weak orderingStrict weak orderingIn mathematics, especially order theory, a strict weak ordering is a binary relation In mathematics, especially order theory, a strict weak ordering is a binary relation ...
– a strict partial order in which incomparability is an equivalence relation - Total ordering – a totalTotal relationIn mathematics, a binary relation R over a set X is total if for all a and b in X, a is related to b or b is related to a .In mathematical notation, this is\forall a, b \in X,\ a R b \or b R a....
, antisymmetricAntisymmetric relationIn mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,...
transitive relation
Counting transitive relations
Unlike other relation properties, no general formula that counts the number of transitive relations on a finite set is known. However, there is a formula for finding the number of relations that are simultaneously reflexive, symmetric, and transitive – in other words, equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
s – , those that are symmetric and transitive, those that are symmetric, transitive, and antisymmetric, and those that are total, transitive, and antisymmetric. Pfeiffer has made some progress in this direction, expressing relations with combinations of these properties in terms of each other, but still calculating any one is difficult. See also.
Examples
- equality
- less/greater than (or equal)
- inclusion of sets
- inequality is not transitive
- being an ancestor of is transitive
- being a parent of is not transitive
See also
- Transitive closureTransitive closureIn mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
- Transitive reductionTransitive reductionIn mathematics, a transitive reduction of a binary relation R on a set X is a minimal relation R' on X such that the transitive closure of R' is the same as the transitive closure of R. If the transitive closure of R is antisymmetric and finite, then R' is unique...
- IntransitivityIntransitivityIn mathematics, the term intransitivity is used for related, but different, properties of binary relations:- Intransitivity :A relation is transitive if, whenever it relates some A to some B, and that B to some C, it also relates that A to that C...
- Reflexive relationReflexive relationIn mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
- Symmetric relationSymmetric relationIn mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...
- Quasitransitive relationQuasitransitive relationQuasitransitivity is a weakened version of transitivity that is used in social choice theory or microeconomics. Informally, a relation is quasitransitive if it is symmetric for some values and transitive elsewhere.-Formal definition:...
External links
- Transitivity in Action at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...

