
Chomsky hierarchy
Encyclopedia
Within the field of computer science
, specifically in the area of formal languages, the Chomsky hierarchy (occasionally referred to as Chomsky–Schützenberger hierarchy) is a containment hierarchy of classes of formal grammar
s.
This hierarchy of grammars was described by Noam Chomsky
in 1956. It is also named after Marcel-Paul Schützenberger
, who played a crucial role in the development of the theory of formal languages
.
A formal grammar defines (or generates) a formal language, which is a (usually infinite) set of finite-length sequences of symbols (i.e. strings
) that may be constructed by applying production rules to another sequence of symbols which initially contains just the start symbol. A rule may be applied to a sequence of symbols by replacing an occurrence of the symbols on the left-hand side of the rule with those that appear on the right-hand side. A sequence of rule applications is called a derivation. Such a grammar defines the formal language: all words consisting solely of terminal symbols which can be reached by a derivation from the start symbol.
Nonterminals are usually represented by uppercase letters, terminals by lowercase letters, and the start symbol by . For example, the grammar with terminals
. For example, the grammar with terminals  , nonterminals
, nonterminals 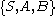 , production rules
, production rules
and start symbol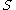 , defines the language of all words of the form
, defines the language of all words of the form 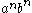 (i.e.
(i.e.  copies of
copies of  followed by
followed by  copies of
copies of 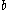 ).
).
The following is a simpler grammar that defines the same language:
Terminals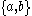 , Nonterminals
, Nonterminals 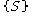 , Start symbol
, Start symbol 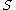 , Production rules
, Production rules
Note that the set of grammars corresponding to recursive language
s is not a member of this hierarchy.
Every regular language is context-free, every context-free language, not containing the empty string, is context-sensitive and every context-sensitive language is recursive and every recursive language is recursively enumerable. These are all proper inclusions, meaning that there exist recursively enumerable languages which are not context-sensitive, context-sensitive languages which are not context-free and context-free languages which are not regular.
The following table summarizes each of Chomsky's four types of grammars, the class of language it generates, the type of automaton that recognizes it, and the form its rules must have.
However, there are further categories of formal languages, some of which are given in the following table:
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, specifically in the area of formal languages, the Chomsky hierarchy (occasionally referred to as Chomsky–Schützenberger hierarchy) is a containment hierarchy of classes of formal grammar
Formal grammar
A formal grammar is a set of formation rules for strings in a formal language. The rules describe how to form strings from the language's alphabet that are valid according to the language's syntax...
s.
This hierarchy of grammars was described by Noam Chomsky
Noam Chomsky
Avram Noam Chomsky is an American linguist, philosopher, cognitive scientist, and activist. He is an Institute Professor and Professor in the Department of Linguistics & Philosophy at MIT, where he has worked for over 50 years. Chomsky has been described as the "father of modern linguistics" and...
in 1956. It is also named after Marcel-Paul Schützenberger
Marcel-Paul Schützenberger
Marcel-Paul "Marco" Schützenberger was a French mathematician and Doctor of Medicine. His work had impact across the fields of formal language, combinatorics, and information theory...
, who played a crucial role in the development of the theory of formal languages
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
.
Formal grammars
A formal grammar of this type consists of:- a finite set of terminal symbols
- a finite set of nonterminal symbols
- a finite set of production rules with a left and a right-hand side consisting of a sequence of these symbols
- a start symbol
A formal grammar defines (or generates) a formal language, which is a (usually infinite) set of finite-length sequences of symbols (i.e. strings
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
) that may be constructed by applying production rules to another sequence of symbols which initially contains just the start symbol. A rule may be applied to a sequence of symbols by replacing an occurrence of the symbols on the left-hand side of the rule with those that appear on the right-hand side. A sequence of rule applications is called a derivation. Such a grammar defines the formal language: all words consisting solely of terminal symbols which can be reached by a derivation from the start symbol.
Nonterminals are usually represented by uppercase letters, terminals by lowercase letters, and the start symbol by
 . For example, the grammar with terminals
. For example, the grammar with terminals  , nonterminals
, nonterminals 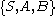 , production rules
, production rules
-
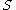

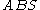
-
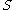
 ε (where ε is the empty string)
ε (where ε is the empty string) -
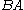

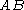
-
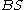
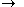
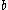
-
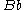
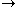

-
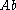


-
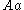
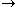
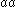
and start symbol
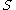 , defines the language of all words of the form
, defines the language of all words of the form 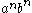 (i.e.
(i.e.  copies of
copies of  followed by
followed by  copies of
copies of 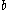 ).
).The following is a simpler grammar that defines the same language:
Terminals
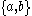 , Nonterminals
, Nonterminals 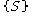 , Start symbol
, Start symbol 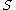 , Production rules
, Production rules
-
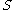
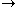
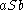
-
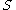
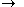 ε
ε
The hierarchy
The Chomsky hierarchy consists of the following levels:- Type-0 grammars (unrestricted grammarUnrestricted grammarIn formal language theory, an unrestricted grammar is a formal grammar on which no restrictions are made on the left and right sides of the grammar's productions...
s) include all formal grammars. They generate exactly all languages that can be recognized by a Turing machineTuring machineA Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
. These languages are also known as the recursively enumerable languageRecursively enumerable languageIn mathematics, logic and computer science, a recursively enumerable language is a type of formal language which is also called partially decidable or Turing-acceptable. It is known as a type-0 language in the Chomsky hierarchy of formal languages...
s. Note that this is different from the recursive languageRecursive languageIn mathematics, logic and computer science, a formal language is called recursive if it is a recursive subset of the set of all possible finite sequences over the alphabet of the language...
s which can be decided by an always-halting Turing machineMachine that always haltsIn computability theory, a machine that always halts—also called a decider or a total Turing machine —is a Turing machine that halts for every input....
. - Type-1 grammars (context-sensitive grammarContext-sensitive grammarA context-sensitive grammar is a formal grammar in which the left-hand sides and right-hand sides of any production rules may be surrounded by a context of terminal and nonterminal symbols...
s) generate the context-sensitive languageContext-sensitive languageIn theoretical computer science, a context-sensitive language is a formal language that can be defined by a context-sensitive grammar. That is one of the four types of grammars in the Chomsky hierarchy...
s. These grammars have rules of the form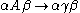 with
with  a nonterminal and
a nonterminal and  ,
, 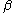 and
and 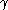 strings of terminals and nonterminals. The strings
strings of terminals and nonterminals. The strings  and
and 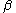 may be empty, but
may be empty, but  must be nonempty. The rule
must be nonempty. The rule  is allowed if
is allowed if 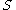 does not appear on the right side of any rule. The languages described by these grammars are exactly all languages that can be recognized by a linear bounded automatonLinear bounded automatonIn computer science, a linear bounded automaton is a restricted form of nondeterministic Turing machine.-Operation:Linear bounded automata satisfy the following three conditions:...
does not appear on the right side of any rule. The languages described by these grammars are exactly all languages that can be recognized by a linear bounded automatonLinear bounded automatonIn computer science, a linear bounded automaton is a restricted form of nondeterministic Turing machine.-Operation:Linear bounded automata satisfy the following three conditions:...
(a nondeterministic Turing machine whose tape is bounded by a constant times the length of the input.) - Type-2 grammars (context-free grammarContext-free grammarIn formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
s) generate the context-free languageContext-free languageIn formal language theory, a context-free language is a language generated by some context-free grammar. The set of all context-free languages is identical to the set of languages accepted by pushdown automata.-Examples:...
s. These are defined by rules of the form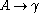 with
with 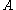 a nonterminal and
a nonterminal and 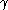 a string of terminals and nonterminals. These languages are exactly all languages that can be recognized by a non-deterministic pushdown automatonPushdown automatonIn automata theory, a pushdown automaton is a finite automaton that can make use of a stack containing data.- Operation :Pushdown automata differ from finite state machines in two ways:...
a string of terminals and nonterminals. These languages are exactly all languages that can be recognized by a non-deterministic pushdown automatonPushdown automatonIn automata theory, a pushdown automaton is a finite automaton that can make use of a stack containing data.- Operation :Pushdown automata differ from finite state machines in two ways:...
. Context-free languages are the theoretical basis for the syntax of most programming languageProgramming languageA programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s. - Type-3 grammars (regular grammarRegular grammarIn theoretical computer science, a regular grammar is a formal grammar that describes a regular language.- Strictly regular grammars :A right regular grammar is a formal grammar such that all the production rules in P are of one of the following forms:# B → a - where B is a non-terminal in N and...
s) generate the regular languageRegular languageIn theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
s. Such a grammar restricts its rules to a single nonterminal on the left-hand side and a right-hand side consisting of a single terminal, possibly followed (or preceded, but not both in the same grammar) by a single nonterminal. The rule is also allowed here if
is also allowed here if  does not appear on the right side of any rule. These languages are exactly all languages that can be decided by a finite state automaton. Additionally, this family of formal languages can be obtained by regular expressions. Regular languages are commonly used to define search patterns and the lexical structure of programming languages.
does not appear on the right side of any rule. These languages are exactly all languages that can be decided by a finite state automaton. Additionally, this family of formal languages can be obtained by regular expressions. Regular languages are commonly used to define search patterns and the lexical structure of programming languages.
Note that the set of grammars corresponding to recursive language
Recursive language
In mathematics, logic and computer science, a formal language is called recursive if it is a recursive subset of the set of all possible finite sequences over the alphabet of the language...
s is not a member of this hierarchy.
Every regular language is context-free, every context-free language, not containing the empty string, is context-sensitive and every context-sensitive language is recursive and every recursive language is recursively enumerable. These are all proper inclusions, meaning that there exist recursively enumerable languages which are not context-sensitive, context-sensitive languages which are not context-free and context-free languages which are not regular.
The following table summarizes each of Chomsky's four types of grammars, the class of language it generates, the type of automaton that recognizes it, and the form its rules must have.
| Grammar | Languages | Automaton | Production rules (constraints) |
|---|---|---|---|
| Type-0 | Recursively enumerable Recursively enumerable language In mathematics, logic and computer science, a recursively enumerable language is a type of formal language which is also called partially decidable or Turing-acceptable. It is known as a type-0 language in the Chomsky hierarchy of formal languages... |
Turing machine Turing machine A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a... |
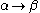 (no restrictions) (no restrictions) |
| Type-1 | Context-sensitive Context-sensitive grammar A context-sensitive grammar is a formal grammar in which the left-hand sides and right-hand sides of any production rules may be surrounded by a context of terminal and nonterminal symbols... |
Linear-bounded non-deterministic Turing machine Linear bounded automaton In computer science, a linear bounded automaton is a restricted form of nondeterministic Turing machine.-Operation:Linear bounded automata satisfy the following three conditions:... |
αAβ ⟶ αγβ |
| Type-2 | Context-free Context-free grammar In formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals .... |
Non-deterministic pushdown automaton Pushdown automaton In automata theory, a pushdown automaton is a finite automaton that can make use of a stack containing data.- Operation :Pushdown automata differ from finite state machines in two ways:... |
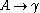 |
| Type-3 | Regular Regular grammar In theoretical computer science, a regular grammar is a formal grammar that describes a regular language.- Strictly regular grammars :A right regular grammar is a formal grammar such that all the production rules in P are of one of the following forms:# B → a - where B is a non-terminal in N and... |
Finite state automaton |  and 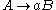 |
However, there are further categories of formal languages, some of which are given in the following table:
External links
- http://www.staff.ncl.ac.uk/hermann.moisl/ell236/lecture5.htm
- "Is chomsky hierarchy outdated/6133" on cstheory.stackexchange.com

