
Recursively enumerable language
Encyclopedia
In mathematics
, logic
and computer science
, a recursively enumerable language is a type of formal language
which is also called partially decidable or Turing-acceptable. It is known as a type-0 language in the Chomsky hierarchy
of formal languages. The class of all recursively enumerable languages is called RE
.
All regular
, context-free
, context-sensitive
and recursive
languages are recursively enumerable.
Post's theorem
shows that RE
, together with its complement
co-RE, correspond to the first level of the arithmetical hierarchy
.
under the following operations. That is, if L and P are two recursively enumerable languages, then the following languages are recursively enumerable as well:
Note that recursively enumerable languages are not closed under set difference or complementation. The set difference L - P may or may not be recursively enumerable. If L is recursively enumerable, then the complement of L is recursively enumerable if and only if L is also recursive.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a recursively enumerable language is a type of formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
which is also called partially decidable or Turing-acceptable. It is known as a type-0 language in the Chomsky hierarchy
Chomsky hierarchy
Within the field of computer science, specifically in the area of formal languages, the Chomsky hierarchy is a containment hierarchy of classes of formal grammars....
of formal languages. The class of all recursively enumerable languages is called RE
RE (complexity)
In computability theory and computational complexity theory, RE is the class of decision problems for which a 'yes' answer can be verified by a Turing machine in a finite amount of time. Informally, it means that if the answer is 'yes', then there is some procedure which takes finite time to...
.
Definitions
There exist three equivalent major definitions for the concept of a recursively enumerable language.- A recursively enumerable formal language is a recursively enumerableRecursively enumerable setIn computability theory, traditionally called recursion theory, a set S of natural numbers is called recursively enumerable, computably enumerable, semidecidable, provable or Turing-recognizable if:...
subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
in the set of all possible words over the alphabetAlphabetAn alphabet is a standard set of letters—basic written symbols or graphemes—each of which represents a phoneme in a spoken language, either as it exists now or as it was in the past. There are other systems, such as logographies, in which each character represents a word, morpheme, or semantic...
of the languageFormal languageA formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
. - A recursively enumerable language is a formal language for which there exists a Turing machineTuring machineA Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
(or other computable functionComputable functionComputable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
) which will enumerate all valid strings of the language. Note that, if the language is infinite, the enumerating algorithm provided can be chosen so that it avoids repetitions, since we can test whether the string produced for number n is "already" produced for a number which is less than n. If it already is produced, use the output for input n+1 instead (recursively), but again, test whether it is "new". - A recursively enumerable language is a formal language for which there exists a Turing machine (or other computable function) that will halt and accept when presented with any string in the language as input but may either halt and reject or loop forever when presented with a string not in the language. Contrast this to recursive languageRecursive languageIn mathematics, logic and computer science, a formal language is called recursive if it is a recursive subset of the set of all possible finite sequences over the alphabet of the language...
s, which require that the Turing machine halts in all cases.
All regular
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
, context-free
Context-free grammar
In formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
, context-sensitive
Context-sensitive language
In theoretical computer science, a context-sensitive language is a formal language that can be defined by a context-sensitive grammar. That is one of the four types of grammars in the Chomsky hierarchy...
and recursive
Recursive language
In mathematics, logic and computer science, a formal language is called recursive if it is a recursive subset of the set of all possible finite sequences over the alphabet of the language...
languages are recursively enumerable.
Post's theorem
Post's theorem
In computability theory Post's theorem, named after Emil Post, describes the connection between the arithmetical hierarchy and the Turing degrees.- Background :The statement of Post's theorem uses several concepts relating to definability and recursion theory...
shows that RE
RE (complexity)
In computability theory and computational complexity theory, RE is the class of decision problems for which a 'yes' answer can be verified by a Turing machine in a finite amount of time. Informally, it means that if the answer is 'yes', then there is some procedure which takes finite time to...
, together with its complement
Complement (complexity)
In computational complexity theory, the complement of a decision problem is the decision problem resulting from reversing the yes and no answers. Equivalently, if we define decision problems as sets of finite strings, then the complement of this set over some fixed domain is its complement...
co-RE, correspond to the first level of the arithmetical hierarchy
Arithmetical hierarchy
In mathematical logic, the arithmetical hierarchy, arithmetic hierarchy or Kleene-Mostowski hierarchy classifies certain sets based on the complexity of formulas that define them...
.
Closure properties
Recursively enumerable languages are closedClosure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under the following operations. That is, if L and P are two recursively enumerable languages, then the following languages are recursively enumerable as well:
- the Kleene starKleene starIn mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
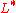 of L
of L - the concatenation
 of L and P
of L and P - the unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...

- the intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....

Note that recursively enumerable languages are not closed under set difference or complementation. The set difference L - P may or may not be recursively enumerable. If L is recursively enumerable, then the complement of L is recursively enumerable if and only if L is also recursive.

