
RE (complexity)
Encyclopedia
In computability theory
and computational complexity theory
, RE (recursively enumerable
) is the class
of decision problem
s for which a 'yes' answer can be verified by a Turing machine
in a finite amount of time. Informally, it means that if the answer is 'yes', then there is some procedure which takes finite time to determine this. On the other hand, if the answer is 'no', the machine might never halt. Equivalently, RE is the class of decision problems for which a Turing machine can list all the 'yes' instances, one by one (this is what 'enumerable' means).
Similarly, co-RE is the set of all languages that are complements of a language in RE. In a sense, co-RE contains languages of which membership can be disproved in a finite amount of time, but proving membership might take forever.
Each member of RE is a recursively enumerable set
and therefore a Diophantine set
.
s (R) is a subset of both RE and co-RE. In fact, it is the intersection of those two classes: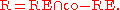
. Generally, no constraint is placed on the reductions used except that they must be many-one reduction
s.
Examples of RE-complete problems:
Examples of co-RE-complete problems:
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
and computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, RE (recursively enumerable
Recursively enumerable set
In computability theory, traditionally called recursion theory, a set S of natural numbers is called recursively enumerable, computably enumerable, semidecidable, provable or Turing-recognizable if:...
) is the class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
of decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
s for which a 'yes' answer can be verified by a Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
in a finite amount of time. Informally, it means that if the answer is 'yes', then there is some procedure which takes finite time to determine this. On the other hand, if the answer is 'no', the machine might never halt. Equivalently, RE is the class of decision problems for which a Turing machine can list all the 'yes' instances, one by one (this is what 'enumerable' means).
Similarly, co-RE is the set of all languages that are complements of a language in RE. In a sense, co-RE contains languages of which membership can be disproved in a finite amount of time, but proving membership might take forever.
Each member of RE is a recursively enumerable set
Recursively enumerable set
In computability theory, traditionally called recursion theory, a set S of natural numbers is called recursively enumerable, computably enumerable, semidecidable, provable or Turing-recognizable if:...
and therefore a Diophantine set
Diophantine set
In mathematics, a Diophantine equation is an equation of the form P=0 where P is a polynomial with integer coefficients...
.
Relations to other classes
The set of recursive languageRecursive language
In mathematics, logic and computer science, a formal language is called recursive if it is a recursive subset of the set of all possible finite sequences over the alphabet of the language...
s (R) is a subset of both RE and co-RE. In fact, it is the intersection of those two classes:
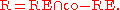
RE-complete
RE-complete is the set of decision problems that are complete for RE. In a sense, these are the "hardest" recursively enumerable problems. All such problems are nonrecursiveRecursive language
In mathematics, logic and computer science, a formal language is called recursive if it is a recursive subset of the set of all possible finite sequences over the alphabet of the language...
. Generally, no constraint is placed on the reductions used except that they must be many-one reduction
Many-one reduction
In computability theory and computational complexity theory, a many-one reduction is a reduction which converts instances of one decision problem into instances of a second decision problem. Reductions are thus used to measure the relative computational difficulty of two problems.Many-one...
s.
Examples of RE-complete problems:
- Halting problemHalting problemIn computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
: Whether a program given a finite input finishes running or will run forever. - By Rice's TheoremRice's theoremIn computability theory, Rice's theorem states that, for any non-trivial property of partial functions, there is no general and effective method to decide whether an algorithm computes a partial function with that property...
, deciding membership in any nontrivial subset of the set of recursive functionsComputable functionComputable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
is RE-hard. It will be complete whenever the set is recursively enumerable. - [Myhill 1955] has proven that all creative sets are RE-complete.
- The uniform word problemWord problem (mathematics)In mathematics and computer science, a word problem for a set S with respect to a system of finite encodings of its elements is the algorithmic problem of deciding whether two given representatives represent the same element of the set...
for groupsGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
or semigroupSemigroupIn mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
s. [Indeed, the word problem for some individual groupsWord problem for groupsIn mathematics, especially in the area of abstract algebra known as combinatorial group theory, the word problem for a finitely generated group G is the algorithmic problem of deciding whether two words in the generators represent the same element...
is RE-complete.] - Deciding membership in a general unrestrictedUnrestricted grammarIn formal language theory, an unrestricted grammar is a formal grammar on which no restrictions are made on the left and right sides of the grammar's productions...
formal grammarFormal grammarA formal grammar is a set of formation rules for strings in a formal language. The rules describe how to form strings from the language's alphabet that are valid according to the language's syntax...
. [Again, certain individual grammars have RE-complete membership problem.] - The validityValidityIn logic, argument is valid if and only if its conclusion is entailed by its premises, a formula is valid if and only if it is true under every interpretation, and an argument form is valid if and only if every argument of that logical form is valid....
problem for first-order logicFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
. - Post correspondence problemPost correspondence problemThe Post correspondence problem is an undecidable decision problem that was introduced by Emil Post in 1946. Because it is simpler than the halting problem and the Entscheidungsproblem it is often used in proofs of undecidability....
: Given a finite set of strings, determine if there is a string that can be factored into a composition of the strings (allowing repeats) in two different ways. - Determining if a Diophantine equationDiophantine equationIn mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
has any integer solutions.
co-RE-complete
co-RE-complete is the set of decision problems that are complete for co-RE. In a sense, these are the complements of the hardest recursively enumerable problems.Examples of co-RE-complete problems:
- The Domino ProblemDomino problemIn geometry, the domino problem is the problem of deciding whether a set of tiles of a particular kind admits a tiling.In a 1961 paper proposing a method for deciding an important case of David Hilbert's Entscheidungsproblem, the logician Hao Wang discussed tiling the plane by equally sized square...
for Wang tileWang tileWang tiles , first proposed by mathematician, logician, and philosopher Hao Wang in 1961, are a class of formal systems...
s. - The satisfiability problem for first-order logicFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...

