Many-one reduction
Encyclopedia
In computability theory
and computational complexity theory
, a many-one reduction is a reduction
which converts instances of one decision problem
into instances of a second decision problem. Reductions are thus used to measure the relative computational difficulty of two problems.
Many-one reductions are a special case and a stronger form of Turing reduction
s. With many-one reductions the oracle can be invoked only once at the end and the answer cannot be modified.
Many-one reductions were first used by Emil Post in 1944. Later Norman Shapiro
used the same concept in 1956 under the name strong reducibility.
s over the alphabet
s Σ and Γ, respectively. A many-one reduction from A to B is a total computable function f : Σ* → Γ* that has the property that
each word w is in A if and only if f(w) is in B (that is,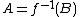
).
If such a function f exists, we say that A is many-one reducible or m-reducible to B and write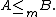
If there is an injective many-one reduction function then we say A is 1 reducible or one-one reducible to B and write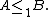
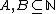we say 
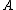is many-one reducible to 
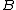and write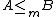
if there exists a total computable function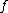
with 
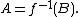
If additionally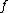
is injective we say 
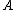is 1-reducible to 
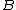and write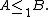
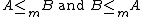
we say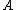
is many-one equivalent or m-equivalent to 
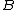and write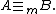
If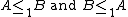
we say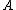
is 1-equivalent to 
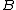and write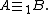
B is recursively enumerable and every recursively enumerable set A is m-reducible to B.
and log-space reduction
for details.
Given decision problems A and B and an algorithm
N which solves instances of B, we can use a many-one reduction from A to B to solve instances of A in:
We say that a class C of languages (or a subset of the power set of the natural numbers) is closed under many-one reducibility if there exists no reduction from a language in C to a language outside C. If a class is closed under many-one reducibility, then many-one reduction can be used to show that a problem is in C by reducing a problem in C to it. Many-one reductions are valuable because most well-studied complexity classes are closed under some type of many-one reducibility, including P
, NP
, L
, NL
, co-NP, PSPACE
, EXP
, and many others. These classes are not closed under arbitrary many-one reductions, however.
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
and computational complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, a many-one reduction is a reduction
Reduction (complexity)
In computability theory and computational complexity theory, a reduction is a transformation of one problem into another problem. Depending on the transformation used this can be used to define complexity classes on a set of problems....
which converts instances of one decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
into instances of a second decision problem. Reductions are thus used to measure the relative computational difficulty of two problems.
Many-one reductions are a special case and a stronger form of Turing reduction
Turing reduction
In computability theory, a Turing reduction from a problem A to a problem B, named after Alan Turing, is a reduction which solves A, assuming B is already known . It can be understood as an algorithm that could be used to solve A if it had available to it a subroutine for solving B...
s. With many-one reductions the oracle can be invoked only once at the end and the answer cannot be modified.
Many-one reductions were first used by Emil Post in 1944. Later Norman Shapiro
Norman Shapiro
Norman Z. Shapiro is an American mathematician,who is the co-author of the Rice–Shapiro theorem.Shapiro spent the summer of 1954 at Bell Laboratories in Murray Hill, New Jerseywhere, in collaboration withKarel de Leeuw,Ed Moore, and...
used the same concept in 1956 under the name strong reducibility.
Formal languages
Suppose A and B are formal languageFormal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
s over the alphabet
Alphabet
An alphabet is a standard set of letters—basic written symbols or graphemes—each of which represents a phoneme in a spoken language, either as it exists now or as it was in the past. There are other systems, such as logographies, in which each character represents a word, morpheme, or semantic...
s Σ and Γ, respectively. A many-one reduction from A to B is a total computable function f : Σ* → Γ* that has the property that
each word w is in A if and only if f(w) is in B (that is,
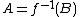).If such a function f exists, we say that A is many-one reducible or m-reducible to B and write
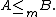
If there is an injective many-one reduction function then we say A is 1 reducible or one-one reducible to B and write
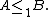
Subsets of natural numbers
Given two sets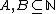 we say 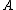is many-one reducible to 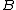and write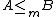if there exists a total computable function
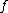with 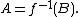If additionally
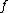is injective we say 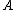is 1-reducible to 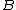and write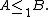Many-one equivalence and 1 equivalence
If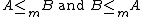we say
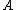is many-one equivalent or m-equivalent to 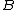and write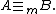If
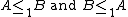
we say
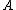is 1-equivalent to 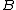and write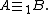Many-one completeness (m-completeness)
A set B is called many-one complete, or simply m-complete, iffIFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
B is recursively enumerable and every recursively enumerable set A is m-reducible to B.
Many-one reductions with resource limitations
Many-one reductions are often subjected to resource restrictions, for example that the reduction function is computable in polynomial time or logarithmic space; see polynomial-time reductionPolynomial-time reduction
In computational complexity theory a polynomial-time reduction is a reduction which is computable by a deterministic Turing machine in polynomial time. If it is a many-one reduction, it is called a polynomial-time many-one reduction, polynomial transformation, or Karp reduction...
and log-space reduction
Log-space reduction
In computational complexity theory, a log-space reduction is a reduction computable by a deterministic Turing machine using logarithmic space. Conceptually, this means it can keep a constant number of pointers into the input, along with a logarithmic number of fixed-size integers...
for details.
Given decision problems A and B and an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
N which solves instances of B, we can use a many-one reduction from A to B to solve instances of A in:
- the time needed for N plus the time needed for the reduction
- the maximum of the space needed for N and the space needed for the reduction
We say that a class C of languages (or a subset of the power set of the natural numbers) is closed under many-one reducibility if there exists no reduction from a language in C to a language outside C. If a class is closed under many-one reducibility, then many-one reduction can be used to show that a problem is in C by reducing a problem in C to it. Many-one reductions are valuable because most well-studied complexity classes are closed under some type of many-one reducibility, including P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
, NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
, L
L (complexity)
In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space...
, NL
NL (complexity)
In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space....
, co-NP, PSPACE
PSPACE
In computational complexity theory, PSPACE is the set of all decision problems which can be solved by a Turing machine using a polynomial amount of space.- Formal definition :...
, EXP
Exp
Exp may stand for:* Exponential function, in mathematics* Expiry date of organic compounds like food or medicines* Experience points, in role-playing games* EXPTIME, a complexity class in computing* Ford EXP, a car manufactured in the 1980s...
, and many others. These classes are not closed under arbitrary many-one reductions, however.
Properties
- The relationRelation (mathematics)In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
s of many-one reducibility and 1 reducibility are transitiveTransitive relationIn mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
and reflexiveReflexive relationIn mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
and thus induce a preorderPreorderIn mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
on the powerset of the natural numbers. -
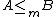if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
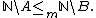
- A set is many-one reducible to the halting problemHalting problemIn computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is recursively enumerable. This says that with regards to many-one reducibility, the halting problem is the most complicated of all computer programs. Thus the halting problem is many-one complete. - The specialized halting problem for an individual Turing machine T (i.e., the set of inputs for which T eventually halts) is many-one complete iff T is a universal Turing machineUniversal Turing machineIn computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
. Emil Post showed that there exist recursively enumerable sets that are neither decidableDecidableThe word decidable may refer to:* Decidable language*Decidability for the equivalent in mathematical logic*Gödel's incompleteness theorem, a theorem on the indecidability of languages consisting of "true statements" in mathematical logic....
nor m-complete, and hence that there exist nonuniversal Turing machines whose individual halting problems are nevertheless undecidable.