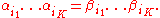Post correspondence problem
Encyclopedia
The Post correspondence problem is an undecidable
decision problem
that was introduced by Emil Post in 1946. Because it is simpler than the halting problem
and the Entscheidungsproblem
it is often used in proofs of undecidability.
and 
of words over some alphabet 
having at least two symbols. A solution to this problem is a sequence
of indices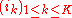
with 
and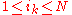 
for all 
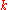, such that
The decision problem then is to decide whether such a solution exists or not.
A solution to this problem would be the sequence (3, 2, 3, 1), because
Furthermore, since (3, 2, 3, 1) is a solution, so are all of its "repetitions", such as (3, 2, 3, 1, 3, 2, 3, 1), etc.; that is, when a solution exists, there are infinitely many solutions of this repetitive kind.
However, if the two lists had consisted of only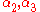
and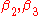 
, then there would have been no solution (because then no matching pair would have the same last letter, as must occur at the end of a solution).
A convenient way to view an instance of a Post correspondence problem is as a collection of blocks of the form
there being an unlimited supply of each type of block. Thus the above example is viewed as
where the solver has an endless supply of each of these three block types. A solution corresponds to some way of laying blocks next to each other so that the string in the top cells corresponds to the string in the bottom cells. Then the solution to the above example corresponds to:
In this instance, every sequence of the form (1, 2, 2, ..., 2, 3) is a solution (in addition to all their repetitions):
on a particular input. A match will only occur if the input would be accepted by the Turing machine. Because deciding if a Turing machine will accept an input is a basic undecidable problem, PCP cannot be decidable either. The following discussion is based on Michael Sipser
's textbook Introduction to the Theory of Computation.
In more detail, the idea is that the string along the top and bottom will be a computation history
of the Turing machine's computation. This means it will list a string describing the initial state, followed by a string describing the next state, and so on until it ends with a string describing an accepting state. The state strings are separated by some separator symbol (usually written #). According to the definition of a Turing machine, the full state of the machine consists of three parts:
Although the tape has infinitely many cells, only some finite prefix of these will be non-blank. We write these down as part of our state. To describe the state of the finite control, we create new symbols, labelled q1 through qk, for each of the finite state machine's k states. We insert the correct symbol into the string describing the tape's contents at the position of the tape head, thereby indicating both the tape head's position and the current state of the finite control. For the alphabet {0,1}, a typical state might look something like:
101101110q700110.
A simple computation history would then look something like this:
q0101#1q401#11q21#1q810.
We start out with this block, where x is the input string and q0 is the start state:
The top starts out "lagging" the bottom by one state, and keeps this lag until the very end stage. Next, for each symbol a in the tape alphabet, as well as #, we have a "copy" block, which copies it unmodified from one state to the next:
We also have a block for each position transition the machine can make, showing how the tape head moves, how the finite state changes, and what happens to the surrounding symbols. For example, here the tape head is over a 0 in state 4, and then writes a 1 and moves right, changing to state 7:
Finally, when the top reaches an accepting state, the bottom needs a chance to finally catch up to complete the match. To allow this, we extend the computation so that once an accepting state is reached, each subsequent machine step will cause a symbol near the tape head to vanish, one at a time, until none remain. If qf is an accepting state, we can represent this with the following transition blocks, where a is a tape alphabet symbol:
There are a number of details to work out, such as dealing with boundaries between states, making sure that our initial tile goes first in the match, and so on, but this shows the general idea of how a static tile puzzle can simulate a Turing machine computation.
Undecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
that was introduced by Emil Post in 1946. Because it is simpler than the halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
and the Entscheidungsproblem
Entscheidungsproblem
In mathematics, the is a challenge posed by David Hilbert in 1928. The asks for an algorithm that will take as input a description of a formal language and a mathematical statement in the language and produce as output either "True" or "False" according to whether the statement is true or false...
it is often used in proofs of undecidability.
Definition of the problem
The input of the problem consists of two finite lists and of words over some alphabet having at least two symbols. A solution to this problem is a sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of indices
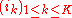with and 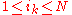for all 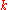, such that
The decision problem then is to decide whether such a solution exists or not.
Example 1
Consider the following two lists:
|
|
A solution to this problem would be the sequence (3, 2, 3, 1), because
Furthermore, since (3, 2, 3, 1) is a solution, so are all of its "repetitions", such as (3, 2, 3, 1, 3, 2, 3, 1), etc.; that is, when a solution exists, there are infinitely many solutions of this repetitive kind.
However, if the two lists had consisted of only
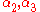and 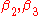, then there would have been no solution (because then no matching pair would have the same last letter, as must occur at the end of a solution).A convenient way to view an instance of a Post correspondence problem is as a collection of blocks of the form
|
there being an unlimited supply of each type of block. Thus the above example is viewed as
|
|
| ||||||
| i = 1 | i = 2 | i = 3 |
where the solver has an endless supply of each of these three block types. A solution corresponds to some way of laying blocks next to each other so that the string in the top cells corresponds to the string in the bottom cells. Then the solution to the above example corresponds to:
|
|
|
| ||||||||
| i1 = 3 | i2 = 2 | i3 = 3 | i4 = 1 |
Example 2
Again using blocks to represent an instance of the problem, the following is an example that has infinitely many solutions in addition to the kind obtained by merely "repeating" a solution.
|
|
| ||||||
| 1 | 2 | 3 |
In this instance, every sequence of the form (1, 2, 2, ..., 2, 3) is a solution (in addition to all their repetitions):
|
|
|
|
| ||||||||||
| 1 | 2 | 2 | 2 | 3 |
Proof sketch of undecidability
The most common proof for the undecidability of PCP describes an instance of PCP that can simulate the computation of a Turing machineTuring machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
on a particular input. A match will only occur if the input would be accepted by the Turing machine. Because deciding if a Turing machine will accept an input is a basic undecidable problem, PCP cannot be decidable either. The following discussion is based on Michael Sipser
Michael Sipser
Michael Fredric Sipser is a professor of Applied Mathematics in the Theory of Computation Group at the Massachusetts Institute of Technology. He received his Ph.D. in 1980 from the University of California, Berkeley under the direction of Manuel Blum....
's textbook Introduction to the Theory of Computation.
In more detail, the idea is that the string along the top and bottom will be a computation history
Computation history
In computer science, a computation history is a sequence of steps taken by an abstract machine in the process of computing its result. Computation histories are frequently used in proofs about the capabilities of certain machines, and particularly about the undecidability of various formal...
of the Turing machine's computation. This means it will list a string describing the initial state, followed by a string describing the next state, and so on until it ends with a string describing an accepting state. The state strings are separated by some separator symbol (usually written #). According to the definition of a Turing machine, the full state of the machine consists of three parts:
- The current contents of the tape.
- The current state of the finite state machineFinite state machineA finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
which operates the tape head. - The current position of the tape head on the tape.
Although the tape has infinitely many cells, only some finite prefix of these will be non-blank. We write these down as part of our state. To describe the state of the finite control, we create new symbols, labelled q1 through qk, for each of the finite state machine's k states. We insert the correct symbol into the string describing the tape's contents at the position of the tape head, thereby indicating both the tape head's position and the current state of the finite control. For the alphabet {0,1}, a typical state might look something like:
101101110q700110.
A simple computation history would then look something like this:
q0101#1q401#11q21#1q810.
We start out with this block, where x is the input string and q0 is the start state:
| q0x# |
The top starts out "lagging" the bottom by one state, and keeps this lag until the very end stage. Next, for each symbol a in the tape alphabet, as well as #, we have a "copy" block, which copies it unmodified from one state to the next:
| a |
| a |
We also have a block for each position transition the machine can make, showing how the tape head moves, how the finite state changes, and what happens to the surrounding symbols. For example, here the tape head is over a 0 in state 4, and then writes a 1 and moves right, changing to state 7:
| q40 |
| 1q7 |
Finally, when the top reaches an accepting state, the bottom needs a chance to finally catch up to complete the match. To allow this, we extend the computation so that once an accepting state is reached, each subsequent machine step will cause a symbol near the tape head to vanish, one at a time, until none remain. If qf is an accepting state, we can represent this with the following transition blocks, where a is a tape alphabet symbol:
|
|
There are a number of details to work out, such as dealing with boundaries between states, making sure that our initial tile goes first in the match, and so on, but this shows the general idea of how a static tile puzzle can simulate a Turing machine computation.
Variants
Many variants of PCP have been considered. One reason is that, when one tries to prove undecidability of some new problem by reducing from PCP, it often happens that the first reduction one finds is not from PCP itself but from an apparently weaker version.- The condition that the alphabet
have at least two symbols is required since the problem is decidable if 
has only one symbol.
- A simple variant is to fix n, the number of tiles. This problem is decidable if n ≤ 2, but remains undecidable for n ≥ 7. It is unknown whether the problem is decidable for 3 ≤ n ≤ 6.
- The circular Post correspondence problem asks whether indexes
can be found such that 
and 
are conjugate words, i.e., they are equal modulo rotation. This variant is undecidable.
- One of the most important variants of PCP is the bounded Post correspondence problem, which asks if we can find a match using no more than k tiles, including repeated tiles. A brute force search solves the problem in time O(2k), but this may be difficult to improve upon, since the problem is NP-completeNP-completeIn computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
. Unlike some NP-complete problems like the boolean satisfiability problemBoolean satisfiability problemIn computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
, a small variation of the bounded problem was also shown to be complete for RNP, which means that it remains hard even if the inputs are chosen at random (it is hard on average over uniformly distributed inputs).
- Another variant of PCP is called the marked Post Correspondence Problem, in which each ui must begin with a different symbol, and each vi must also begin with a different symbol. Halava, Hirvensalo, and de Wolf showed that this variation is decidable in exponential timeEXPTIMEIn computational complexity theory, the complexity class EXPTIME is the set of all decision problems solvable by a deterministic Turing machine in O time, where p is a polynomial function of n....
. Moreover, they showed that if this requirement is slightly loosened so that only the two-character prefixes need to differ (the so-called 2-marked Post Correspondence Problem), the problem becomes undecidable again.
- The Post Embedding Problem is another variant where one looks for indexes
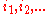such that 
is a (scattered) subwordSubstringA subsequence, substring, prefix or suffix of a string is a subset of the symbols in a string, where the order of the elements is preserved...
of
. This variant is easily decidable since, when some solutions exist, in particular a length-one solution exists. More interesting is the Regular Post Embedding Problem, a further variant where one looks for solutions that belong to a given regular language (submitted, e.g., under the form of a regular expression on the set 
). The Regular Post Embedding Problem is still decidable but, because of the added regular constraint, it has a very high complexity that dominates every multiply recursive function.
External links
- Eitan M. Gurari. An Introduction to the Theory of Computation, Chapter 4, Post's Correspondence Problem. A proof of the undecidability of PCP based on a generalization of context-free grammarContext-free grammarIn formal language theory, a context-free grammar is a formal grammar in which every production rule is of the formwhere V is a single nonterminal symbol, and w is a string of terminals and/or nonterminals ....
s. - Online PHP Based PCP Solver
- PCP AT HOME