Regular language
Encyclopedia
In theoretical computer science
and formal language theory, a regular language is a formal language
that can be expressed using regular expression
.
Note that the "regular expression" features provided with many programming languages are augmented with features that make them capable of recognizing languages that
can not be expressed by the formal regular expressions (as formally defined below).
In chomsky hierarchy
, regular languages are defined to be the languages that
are generated by Type-3 grammars (regular grammar
s).
Regular languages are very useful in input parsing
and programming language
design.
See regular expression for its syntax and semantics. Note that the above cases are in effect the defining rules of regular expression.
Examples
All finite languages are regular. Other typical examples include the language consisting of all strings over the alphabet {a, b} which contain an even number of as, or the language consisting of all strings of the form: several as followed by several bs.
A simple example of a language that is not regular is the set of strings
. This is because in this language, the number of as controls the number of bs, which is not allowed by any of the above rules.
The above properties are sometimes used as alternative definition of regular languages.
, the complexity class
of all regular languages is sometimes referred to as REGULAR or REG and equals DSPACE
(O(1)), the decision problem
s that can be solved in constant space (the space used is independent of the input size). REGULAR ≠ AC0
, since it (trivially) contains the parity problem of determining whether the number of 1 bits in the input is even or odd and this problem is not in AC0. On the other hand, REGULAR does not contain AC0, because the nonregular language of palindrome
s, or the nonregular language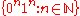
can both be recognized in AC0.
If a language is not regular, it requires a machine with at least Ω
(log log n) space to recognize (where n is the input size). In other words, DSPACE(o
(log log n)) equals the class of regular languages. In practice, most nonregular problems are solved by machines taking at least logarithmic space.
under the various operations, that is, if the languages K and L are regular, so is the result of the following operations:
, one notices that every regular language is context-free. The converse is not true: for example the language consisting of all strings having the same number of a' s as b' s is context-free but not regular. To prove that a language such as this is not regular, one uses the Myhill–Nerode theorem
or the pumping lemma
.
There are two purely algebraic approaches to define regular languages. If:
then the set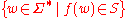
is regular. Every regular language arises in this fashion.
If L is any subset of Σ*, one defines an equivalence relation
~ (called the syntactic relation) on Σ* as follows: u ~ v is defined to mean
The language L is regular if and only if the number of equivalence classes of ~ is finite (A proof of this is provided in the article on the syntactic monoid
). When a language is regular, then the number of equivalence classes is equal to the number of states of the minimal deterministic finite automaton
accepting L.
A similar set of statements can be formulated for a monoid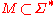
. In this case, equivalence over M leads to the concept of a recognizable language
.
that is the union
of every word in the language.
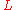there exist constants 
and polynomials 
such that for every
the number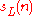 
of words of length 
in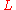 
satisfies the equation
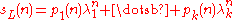. Thus, a non-regularity of some language 
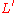can be proved by counting the words in
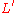. Consider, for example, the Dyck language
of strings of balanced parentheses. The number of words of length
in the Dyck language is equal to the Catalan number
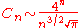, which is not of the form 
,
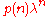witnessing the non-regularity of the Dyck language.
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
and formal language theory, a regular language is a formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
that can be expressed using regular expression
Regular expression
In computing, a regular expression provides a concise and flexible means for "matching" strings of text, such as particular characters, words, or patterns of characters. Abbreviations for "regular expression" include "regex" and "regexp"...
.
Note that the "regular expression" features provided with many programming languages are augmented with features that make them capable of recognizing languages that
can not be expressed by the formal regular expressions (as formally defined below).
In chomsky hierarchy
Chomsky hierarchy
Within the field of computer science, specifically in the area of formal languages, the Chomsky hierarchy is a containment hierarchy of classes of formal grammars....
, regular languages are defined to be the languages that
are generated by Type-3 grammars (regular grammar
Regular grammar
In theoretical computer science, a regular grammar is a formal grammar that describes a regular language.- Strictly regular grammars :A right regular grammar is a formal grammar such that all the production rules in P are of one of the following forms:# B → a - where B is a non-terminal in N and...
s).
Regular languages are very useful in input parsing
Parsing
In computer science and linguistics, parsing, or, more formally, syntactic analysis, is the process of analyzing a text, made of a sequence of tokens , to determine its grammatical structure with respect to a given formal grammar...
and programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
design.
Formal definition
The collection of regular languages over an alphabet Σ is defined recursively as follows:- The empty language Ø is a regular language.
- The empty stringEmpty stringIn computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....
language {ε} is a regular language. - For each a ∈ Σ (a belongs to Σ), the singleton language {a} is a regular language.
- If A and B are regular languages, then A ∪ B (union), A • B (concatenation), and A* (Kleene starKleene starIn mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
) are regular languages. - No other languages over Σ are regular.
See regular expression for its syntax and semantics. Note that the above cases are in effect the defining rules of regular expression.
Examples
All finite languages are regular. Other typical examples include the language consisting of all strings over the alphabet {a, b} which contain an even number of as, or the language consisting of all strings of the form: several as followed by several bs.
A simple example of a language that is not regular is the set of strings
. This is because in this language, the number of as controls the number of bs, which is not allowed by any of the above rules.Equivalence to other formalisms
A regular language satisfies the following equivalent properties:- it can be accepted by a deterministic finite automaton.
- it can be accepted by a nondeterministic finite automaton.
- it can be accepted by an alternating finite automatonAlternating finite automatonIn automata theory, an alternating finite automaton is a nondeterministic finite automaton whose transitions are divided into existential and universal transitions. For example, let A be an alternating automaton....
. - it can be generated by a regular grammarRegular grammarIn theoretical computer science, a regular grammar is a formal grammar that describes a regular language.- Strictly regular grammars :A right regular grammar is a formal grammar such that all the production rules in P are of one of the following forms:# B → a - where B is a non-terminal in N and...
- it can be generated by a prefix grammarPrefix grammarIn computer science, a prefix grammar is a type of string rewriting system, consisting of a set of string rewriting rules, and similar to a formal grammar or a semi-Thue system. What is specific about prefix grammars is not the shape of their rules, but the way in which they are applied: only...
- it can be accepted by a read-only Turing machineTuring machineA Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
- it can be defined in monadicMonadic predicate calculusIn logic, the monadic predicate calculus is the fragment of predicate calculus in which all predicate letters are monadic , and there are no function letters...
second-order logicSecond-order logicIn logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory.... - it is recognized by some finitely generated monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
- it is the preimage of a subset of a finite monoid under a homomorphism from the free monoid on its alphabet
The above properties are sometimes used as alternative definition of regular languages.
Complexity results
In computational complexity theoryComputational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, the complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
of all regular languages is sometimes referred to as REGULAR or REG and equals DSPACE
DSPACE
In computational complexity theory, DSPACE or SPACE is the computational resource describing the resource of memory space for a deterministic Turing machine. It represents the total amount of memory space that a "normal" physical computer would need to solve a given computational problem with a...
(O(1)), the decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
s that can be solved in constant space (the space used is independent of the input size). REGULAR ≠ AC0
AC0
AC0 is a complexity class used in circuit complexity. It is the smallest class in the AC hierarchy, and consists of all families of circuits of depth O and polynomial size, with unlimited-fanin AND gates and OR gates....
, since it (trivially) contains the parity problem of determining whether the number of 1 bits in the input is even or odd and this problem is not in AC0. On the other hand, REGULAR does not contain AC0, because the nonregular language of palindrome
Palindrome
A palindrome is a word, phrase, number, or other sequence of units that can be read the same way in either direction, with general allowances for adjustments to punctuation and word dividers....
s, or the nonregular language
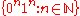can both be recognized in AC0.If a language is not regular, it requires a machine with at least Ω
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(log log n) space to recognize (where n is the input size). In other words, DSPACE(o
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
(log log n)) equals the class of regular languages. In practice, most nonregular problems are solved by machines taking at least logarithmic space.
Closure properties
The regular languages are closedClosure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under the various operations, that is, if the languages K and L are regular, so is the result of the following operations:
- the set theoretic Boolean operations: unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
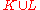, intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
, and complementComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
. From this also differenceDifferenceDifference may refer to:* Difference , a 2005 power metal album* Difference , a concept in computer science* Difference , any systematic way of distinguishing similar coats of arms belonging to members of the same family* Difference , a statement about the relative size or order of two objects**...
follows. - the regular operations: unionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
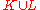, concatenationConcatenationIn computer programming, string concatenation is the operation of joining two character strings end-to-end. For example, the strings "snow" and "ball" may be concatenated to give "snowball"...
, and Kleene starKleene starIn mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
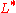. - the trioAbstract family of languagesIn computer science, in particular in the field of formal language theory,the term abstract family of languages refers to an abstract mathematical notion generalizing characteristics common to the regular languages, the context-free languages and the recursively enumerable languages, and other...
operations: string homomorphism, inverse string homomorphism, and intersection with regular languages. As a consequence they are closed under arbitrary finite state transductionsFinite state transducerA finite state transducer is a finite state machine with two tapes: an input tape and an output tape. This contrasts with an ordinary finite state automaton , which has a single tape.-Overview:...
, like quotientRight quotientThe right quotient of a formal language L_1 with a formal language L_2 is the language consisting of strings w such that wx is in L_1 for some string x in L_2...
with a regular language. Even more, regular languages are closed under quotients with arbitrary languages: If L is regular then L/K is regular for any K. - the reverse (or mirror image)
.
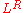Deciding whether a language is regular
To locate the regular languages in the Chomsky hierarchyChomsky hierarchy
Within the field of computer science, specifically in the area of formal languages, the Chomsky hierarchy is a containment hierarchy of classes of formal grammars....
, one notices that every regular language is context-free. The converse is not true: for example the language consisting of all strings having the same number of a
Myhill–Nerode theorem
In the theory of formal languages, the Myhill–Nerode theorem provides a necessary and sufficient condition for a language to be regular. The theorem is named for John Myhill and Anil Nerode, who proved it at the University of Chicago in 1958 ....
or the pumping lemma
Pumping lemma
In the theory of formal languages in computability theory, a pumping lemma or pumping argument states that, for a particular language to be a member of a language class, any sufficiently long string in the language contains a section, or sections, that can be removed, or repeated any number of...
.
There are two purely algebraic approaches to define regular languages. If:
- Σ is a finite alphabet,
- Σ* denotes the free monoid over Σ consisting of all strings over Σ,
- f : Σ* → M is a monoid homomorphism where M is a finite monoid,
- S is a subset of M
then the set
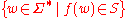is regular. Every regular language arises in this fashion.If L is any subset of Σ*, one defines an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
~ (called the syntactic relation) on Σ* as follows: u ~ v is defined to mean
- uw ∈ L if and only if vw ∈ L for all w ∈ Σ*
The language L is regular if and only if the number of equivalence classes of ~ is finite (A proof of this is provided in the article on the syntactic monoid
Syntactic monoid
In mathematics and computer science, the syntactic monoid M of a formal language L is the smallest monoid that recognizes the language L.-Syntactic quotient:...
). When a language is regular, then the number of equivalence classes is equal to the number of states of the minimal deterministic finite automaton
Dfa minimization
In computer science, more specifically in the branch of automata theory, DFA minimization is the task of transforming a given deterministic finite automaton into an equivalent DFA that has minimum number of states. Here, two DFAs are called equivalent if they describe the same regular language...
accepting L.
A similar set of statements can be formulated for a monoid
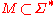. In this case, equivalence over M leads to the concept of a recognizable languageRecognizable language
In mathematics and computer science, a recognizable language is a formal language that is recognized by a finite state machine. Equivalently, a recognizable language is one for which the family of quotients for the syntactic relation is finite.-Definition:...
.
Finite languages
A specific subset within the class of regular languages is the finite languages – those containing only a finite number of words. These are regular languages, as one can create a regular expressionRegular expression
In computing, a regular expression provides a concise and flexible means for "matching" strings of text, such as particular characters, words, or patterns of characters. Abbreviations for "regular expression" include "regex" and "regexp"...
that is the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of every word in the language.
The number of words in a regular language
For any regular language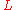 there exist constants and polynomials such that for every
the number 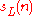of words of length in 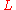satisfies the equation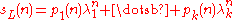. Thus, a non-regularity of some language 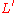can be proved by counting the words in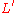. Consider, for example, the Dyck languageDyck language
In the theory of formal languages of computer science, mathematics, and linguistics, the Dyck language is the language consisting of balanced strings of parentheses [ and ]. It is important in the parsing of expressions that must have a correctly nested sequence of parentheses, such as arithmetic...
of strings of balanced parentheses. The number of words of length
in the Dyck language is equal to the Catalan number
Catalan number
In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...
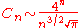, which is not of the form 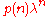,witnessing the non-regularity of the Dyck language.