
Finite state transducer
Encyclopedia
A finite state transducer (FST) is a finite state machine
with two tapes: an input tape and an output tape. This contrasts with an ordinary finite state automaton (or finite state acceptor), which has a single tape.
, which is a set of strings. The two views of automata are equivalent: the function that the automaton computes is precisely the indicator function of the set of strings it generates. The class of languages generated by finite automata is known as the class of regular language
s.
The two tapes of a transducer are typically viewed as an input tape and an output tape. On this view, a transducer is said to transduce (i.e., translate) the contents of its input tape to its output tape, by accepting a string on its input tape and generating another string on its output tape. It may do so nondeterministically and it may produce more than one output for each input string. A transducer may also produce no output for a given input string, in which case it is said to reject the input. In general, a transducer computes a relation
between two formal languages. The class of relations computed by finite state transducers is known as the class of rational relations.
Finite-state transducers are often used for phonological
and morphological analysis
in natural language processing
research and applications. Pioneers in this field include Ronald Kaplan
, Lauri Karttunen, Martin Kay
and Kimmo Koskenniemi
.
A common way of using transducers is in a so-called "cascade", where transducers for various operations are combined into a single transducer by repeated application of the composition operator (defined below).
We can view (Q, δ) as a labeled directed graph
, known as the transition graph of T: the set of vertices is Q, and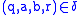 means that there is a labeled edge going from vertex q to vertex r. We also say that a is the input label and b the output label of that edge.
means that there is a labeled edge going from vertex q to vertex r. We also say that a is the input label and b the output label of that edge.
NOTE: This definition of finite transducer is also called letter transducer (Roche and Schabes 1997); alternative definitions are possible, but can all be converted into transducers following this one.
Define the extended transition relation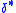 as the smallest set such that:
as the smallest set such that:
The extended transition relation is essentially the reflexive transitive closure
of the transition graph that has been augmented to take edge labels into account. The elements of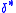 are known as paths. The edge labels of a path are obtained by concatenating the edge labels of its constituent transitions in order.
are known as paths. The edge labels of a path are obtained by concatenating the edge labels of its constituent transitions in order.
The behavior of the transducer T is the rational relation [T] defined as follows: if and only if
if and only if
there exists and
and 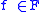 such that
such that 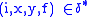 . This is to say that T transduces a string
. This is to say that T transduces a string 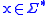 into a string
into a string 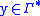 if there exists a path from an initial state to a final state whose input label is x and whose output label is y.
if there exists a path from an initial state to a final state whose input label is x and whose output label is y.
Finite State Transducers can be weighted, where each transition is labeled with a weight in addition to the input and output labels. This property makes FSTs very useful for machine learning applications. A Weighted Finite State Transducer (WFST) over a semiring
K can be defined similarly to an unweighted one as an 8-tuple T=(Q, Σ, Γ, I, F, E, λ, ρ), where:
In order to make certain operations on WFSTs well-defined, the weights have to form a Semiring
. Two typical semirings used in practice are Log and Tropical Semirings.
Finite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
with two tapes: an input tape and an output tape. This contrasts with an ordinary finite state automaton (or finite state acceptor), which has a single tape.
Overview
An automaton can be said to recognize a string if we view the content of its tape as input. In other words, the automaton computes a function that maps strings into the set {0,1}. Alternatively, we can say that an automaton generates strings, which means viewing its tape as an output tape. On this view, the automaton generates a formal languageFormal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
, which is a set of strings. The two views of automata are equivalent: the function that the automaton computes is precisely the indicator function of the set of strings it generates. The class of languages generated by finite automata is known as the class of regular language
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
s.
The two tapes of a transducer are typically viewed as an input tape and an output tape. On this view, a transducer is said to transduce (i.e., translate) the contents of its input tape to its output tape, by accepting a string on its input tape and generating another string on its output tape. It may do so nondeterministically and it may produce more than one output for each input string. A transducer may also produce no output for a given input string, in which case it is said to reject the input. In general, a transducer computes a relation
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
between two formal languages. The class of relations computed by finite state transducers is known as the class of rational relations.
Finite-state transducers are often used for phonological
Phonology
Phonology is, broadly speaking, the subdiscipline of linguistics concerned with the sounds of language. That is, it is the systematic use of sound to encode meaning in any spoken human language, or the field of linguistics studying this use...
and morphological analysis
Morphology (linguistics)
In linguistics, morphology is the identification, analysis and description, in a language, of the structure of morphemes and other linguistic units, such as words, affixes, parts of speech, intonation/stress, or implied context...
in natural language processing
Natural language processing
Natural language processing is a field of computer science and linguistics concerned with the interactions between computers and human languages; it began as a branch of artificial intelligence....
research and applications. Pioneers in this field include Ronald Kaplan
Ronald Kaplan
Ronald M. Kaplan is Chief Scientist and a Principal Researcher at the Powerset division of Microsoft Bing. He is also a Consulting Professor in the Linguistics Department at Stanford University and a Principal of Stanford's Center for the Study of Language and Information...
, Lauri Karttunen, Martin Kay
Martin Kay
Martin Kay is a computer scientist known especially for his work in computational linguistics.Born and raised in the United Kingdom, he received his M.A. from Trinity College, Cambridge, in 1961. In 1958 he started to work at the Cambridge Language Research Unit, one of the earliest centers for...
and Kimmo Koskenniemi
Kimmo Koskenniemi
Kimmo Matti Koskenniemi is the inventor of finite-state two-level models for computational phonology and morphology and a professor of Computational Linguistics at the University of Helsinki, Finland.- Bibliography :...
.
A common way of using transducers is in a so-called "cascade", where transducers for various operations are combined into a single transducer by repeated application of the composition operator (defined below).
Formal construction
Formally, a finite transducer T is a 6-tuple (Q, Σ, Γ, I, F, δ) such that:- Q is a finite set, the set of states;
- Σ is a finite set, called the input alphabet;
- Γ is a finite set, called the output alphabet;
- I is a subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of Q, the set of initial states; - F is a subset of Q, the set of final states; and
-
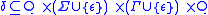 (where ε is the empty stringEmpty stringIn computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....
(where ε is the empty stringEmpty stringIn computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....
) is the transition relation.
We can view (Q, δ) as a labeled directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
, known as the transition graph of T: the set of vertices is Q, and
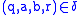 means that there is a labeled edge going from vertex q to vertex r. We also say that a is the input label and b the output label of that edge.
means that there is a labeled edge going from vertex q to vertex r. We also say that a is the input label and b the output label of that edge.NOTE: This definition of finite transducer is also called letter transducer (Roche and Schabes 1997); alternative definitions are possible, but can all be converted into transducers following this one.
Define the extended transition relation
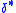 as the smallest set such that:
as the smallest set such that:-
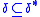 ;
; -
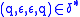 for all
for all 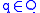 ; and
; and - whenever
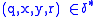 and
and  then
then 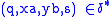 .
.
The extended transition relation is essentially the reflexive transitive closure
Transitive closure
In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
of the transition graph that has been augmented to take edge labels into account. The elements of
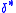 are known as paths. The edge labels of a path are obtained by concatenating the edge labels of its constituent transitions in order.
are known as paths. The edge labels of a path are obtained by concatenating the edge labels of its constituent transitions in order.The behavior of the transducer T is the rational relation [T] defined as follows:
 if and only if
if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there exists
 and
and 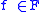 such that
such that 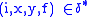 . This is to say that T transduces a string
. This is to say that T transduces a string 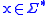 into a string
into a string 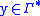 if there exists a path from an initial state to a final state whose input label is x and whose output label is y.
if there exists a path from an initial state to a final state whose input label is x and whose output label is y.Finite State Transducers can be weighted, where each transition is labeled with a weight in addition to the input and output labels. This property makes FSTs very useful for machine learning applications. A Weighted Finite State Transducer (WFST) over a semiring
Semiring
In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
K can be defined similarly to an unweighted one as an 8-tuple T=(Q, Σ, Γ, I, F, E, λ, ρ), where:
- Q, Σ, Γ, I, F are defined as above;
-
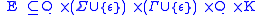 (where ε is the empty stringEmpty stringIn computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....
(where ε is the empty stringEmpty stringIn computer science and formal language theory, the empty string is the unique string of length zero. It is denoted with λ or sometimes Λ or ε....
) is the finite set of transitions; -
 maps initial states to weights;
maps initial states to weights; -
 maps final states to weights.
maps final states to weights.
In order to make certain operations on WFSTs well-defined, the weights have to form a Semiring
Semiring
In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
. Two typical semirings used in practice are Log and Tropical Semirings.
Operations on finite state transducers
The following operations defined on finite automata also apply to finite transducers:- UnionUnion (set theory)In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
. Given transducers T and S, there exists a transducer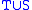 such that
such that  if and only if
if and only if 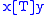 or
or 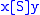 .
.
- Concatenation. Given transducers T and S, there exists a transducer
 such that
such that 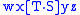 if and only if
if and only if 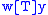 and
and  .
.
- Kleene closure. Given a transducer T, there exists a transducer
 with the following properties: (1)
with the following properties: (1) 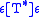 ; (2) if
; (2) if 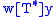 and
and 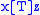 then
then 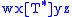 ; and
; and 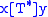 does not hold unless mandated by (1) or (2).
does not hold unless mandated by (1) or (2).
- IntersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
. Given transducers T, S, the intersection of these transducers H has the property that (1) x[H]y if and only if x[T]y and x[S]y.
- CompositionComposition of relationsIn mathematics, the composition of binary relations is a concept of forming a new relation from two given relations R and S, having as its most well-known special case the composition of functions.- Definition :...
. Given a transducer T on alphabets Σ and Γ and a transducer S on alphabets Γ and Δ, there exists a transducer on Σ and Δ such that
on Σ and Δ such that 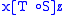 if and only if there exists a string
if and only if there exists a string  such that
such that 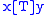 and
and 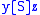 . This operation extends to the weighted case.
. This operation extends to the weighted case.
- This definition uses the same notation which is used in mathematics for relation compositionComposition of relationsIn mathematics, the composition of binary relations is a concept of forming a new relation from two given relations R and S, having as its most well-known special case the composition of functions.- Definition :...
. However, the conventional reading for relation composition is the other way around: given two relations and
and  ,
, 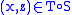 when there exist some
when there exist some  such that
such that 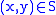 and
and 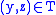 .
.
- ProjectionProjection (mathematics)Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
to an automaton. There are two projection functions: preserves the input tape, and
preserves the input tape, and 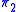 preserves the output tape. The first projection,
preserves the output tape. The first projection,  is defined as follows:
is defined as follows:
- Given a transducer T, there exists a finite automaton
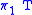 such that
such that 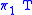 accepts x if and only if there exists a string y for which
accepts x if and only if there exists a string y for which  .
.
- The second projection,
 is defined similarly.
is defined similarly.
- Determinization. Given a transducer T, we want to build an equivalent transducer which has a unique initial state and such that no two transitions leaving any state share the same input label. The powerset constructionPowerset constructionIn the theory of computation and Automata theory, the powerset construction or subset construction is a standard method for converting a nondeterministic finite automaton into a deterministic finite automaton which recognizes the same formal language...
can be extended to transducers, or even weighted transducers, but sometimes fails to halt; indeed, some non-deterministic transducers do not admit equivalent deterministic transducers. CharacterizationsCharacterization (mathematics)In mathematics, the statement that "Property P characterizes object X" means, not simply that X has property P, but that X is the only thing that has property P. It is also common to find statements such as "Property Q characterises Y up to isomorphism". The first type of statement says in...
of determinizable transducers have been proposed along with efficient algorithms to test them: they rely on the semiringSemiringIn abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
used in the weighted case as well as a general property on the structure of the transducer (the twins property).
- Weight pushing for the weighted case.
- Minimization for the weighted case.
- Removal of epsilon-transitions.
Additional properties of finite state transducers
- It is decidableDecidableThe word decidable may refer to:* Decidable language*Decidability for the equivalent in mathematical logic*Gödel's incompleteness theorem, a theorem on the indecidability of languages consisting of "true statements" in mathematical logic....
whether the relation [T] of a transducer T is empty.
- It is decidable whether there exists a string y such that x[T]y for a given string x.
- It is undecidableUndecidableUndecidable may refer to:In mathematics and logic* Undecidable problem - a decision problem which no algorithm can decide* "Undecidable" is sometimes used as a synonym of "independent", where a formula in mathematical logic is independent of a logical theory if neither that formula nor its negation...
whether two transducers are equivalent.
- If one defines the alphabet of labels
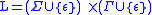 , finite state transducers are isomorphic to NDFA over the alphabet
, finite state transducers are isomorphic to NDFA over the alphabet  , and may therefore be determinized (turned into deterministic finite state machineDeterministic finite state machineIn the theory of computation and automata theory, a deterministic finite state machine—also known as deterministic finite automaton —is a finite state machine accepting finite strings of symbols. For each state, there is a transition arrow leading out to a next state for each symbol...
, and may therefore be determinized (turned into deterministic finite state machineDeterministic finite state machineIn the theory of computation and automata theory, a deterministic finite state machine—also known as deterministic finite automaton —is a finite state machine accepting finite strings of symbols. For each state, there is a transition arrow leading out to a next state for each symbol...
s over the alphabet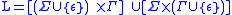 ) and subsequently minimized so that they have the minimum number of states.
) and subsequently minimized so that they have the minimum number of states.
Internal links
- Mealy machineMealy machineIn the theory of computation, a Mealy machine is a finite-state machine whose output values are determined both by its current state and the current inputs. The outputs change asynchronously with respect to the clock, meaning that the outputs change at unpredictable times, making timing analysis...
- Moore machineMoore machineIn the theory of computation, a Moore machine is a finite-state machine, whose output values are determined solely by its current state.-Name:The Moore machine is named after Edward F...
- Morphological dictionaryMorphological dictionaryIn the field of computational linguistics, a morphological dictionary is a file that contains correspondences between surface form and lexical forms of words. Surface forms of words are those found in any text. The corresponding lexical form of a surface form is the lemma followed by grammatical...
- foma (software)Foma (software)Foma is a free and open source finite-state toolkit created and maintained by Mans Hulden. It includes a compiler, programming language, and C library for constructing finite-state automata and transducers for various uses, most typically Natural Language Processing uses such as morphological...

