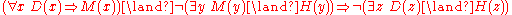Monadic predicate calculus
Encyclopedia
In logic
, the monadic predicate calculus is the fragment of predicate calculus in which all predicate letters are monadic (that is, they take only one argument), and there are no function letters. All atomic formula
e have the form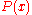 , where
, where 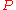 is a predicate letter and
is a predicate letter and  is a variable
is a variable
.
Monadic predicate logic can be contrasted with polyadic predicate logic, which uses predicates (called many-place predicates) that take two or more arguments. For example, "x is mortal" or "Mx" is a one-place predicate, while "x loves y" or "Lxy" is a two-place predicate and "x lies between y and z" or "Bxyz" is a three-place predicate.
The absence of polyadic predicates severely restricts what can be expressed in the monadic predicate calculus. That calculus is so weak that, unlike the full predicate calculus, it is decidable
whether a given formula of that calculus is logically valid (true for all nonempty domain
s). (However, adding a single binary predicate letter to monadic logic would result in a system with the expressive power of the full predicate calculus.) Because the monadic predicate calculus is decidable
, it is ipso facto inadequate for general mathematical reasoning, if only because the tiny fragment of mathematics called Peano arithmetic is known to be undecidable.
Notwithstanding the above deficiencies, the need to go beyond monadic logic was not appreciated until the work on the logic of relation
s, by Augustus DeMorgan and Charles Sanders Peirce in the 19th century, and by Frege in his little-read 1879 Begriffsschrifft. Prior to the work of these three men, syllogistic term logic
was widely considered adequate for formal deductive reasoning.
Inferences in term logic can all be represented in the monadic predicate calculus. For example the syllogism
can be notated in the language of monadic predicate calculus as
where ,
,  and
and  denote the predicates of being, respectively, a dog, a mammal, and a herbivore.
denote the predicates of being, respectively, a dog, a mammal, and a herbivore.
Conversely, monadic predicate calculus is not significantly more expressive than term logic. It is easily proved that every formula in the monadic predicate calculus is equivalent
to a formula in which quantifiers appear only in closed subformulae of the form

or
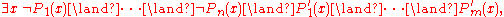
Each of these formulas is the negation of the other, and the quantifiers do not nest. These formulas also generalize slightly the form of basic judgements considered in term logic. For example, this form allows statements such as "Every mammal is either a herbivore or a carnivore (or both)",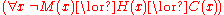 . Reasoning about such statements can, however, still be handled within the framework of term logic, although not by the 19 classical Aristotelian syllogism
. Reasoning about such statements can, however, still be handled within the framework of term logic, although not by the 19 classical Aristotelian syllogism
s alone.
Taking propositional logic as given, every formula in the monadic predicate calculus expresses something that can likewise be formulated in term logic. On the other hand, a modern view of the problem of multiple generality
in traditional logic concludes that quantifiers cannot nest usefully if there are no polyadic predicates to relate the bound variables.
Monadic predicate calculus is also called monadic first-order logic. Monadic second-order logic
keeps the requirement that all predicates be unary, but allows for quantification over predicates as well as variables.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, the monadic predicate calculus is the fragment of predicate calculus in which all predicate letters are monadic (that is, they take only one argument), and there are no function letters. All atomic formula
Atomic formula
In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...
e have the form
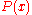 , where
, where 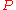 is a predicate letter and
is a predicate letter and  is a variable
is a variableVariable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
.
Monadic predicate logic can be contrasted with polyadic predicate logic, which uses predicates (called many-place predicates) that take two or more arguments. For example, "x is mortal" or "Mx" is a one-place predicate, while "x loves y" or "Lxy" is a two-place predicate and "x lies between y and z" or "Bxyz" is a three-place predicate.
The absence of polyadic predicates severely restricts what can be expressed in the monadic predicate calculus. That calculus is so weak that, unlike the full predicate calculus, it is decidable
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
whether a given formula of that calculus is logically valid (true for all nonempty domain
Domain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
s). (However, adding a single binary predicate letter to monadic logic would result in a system with the expressive power of the full predicate calculus.) Because the monadic predicate calculus is decidable
Decidability (logic)
In logic, the term decidable refers to the decision problem, the question of the existence of an effective method for determining membership in a set of formulas. Logical systems such as propositional logic are decidable if membership in their set of logically valid formulas can be effectively...
, it is ipso facto inadequate for general mathematical reasoning, if only because the tiny fragment of mathematics called Peano arithmetic is known to be undecidable.
Notwithstanding the above deficiencies, the need to go beyond monadic logic was not appreciated until the work on the logic of relation
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
s, by Augustus DeMorgan and Charles Sanders Peirce in the 19th century, and by Frege in his little-read 1879 Begriffsschrifft. Prior to the work of these three men, syllogistic term logic
Term logic
In philosophy, term logic, also known as traditional logic or aristotelian logic, is a loose name for the way of doing logic that began with Aristotle and that was dominant until the advent of modern predicate logic in the late nineteenth century...
was widely considered adequate for formal deductive reasoning.
Inferences in term logic can all be represented in the monadic predicate calculus. For example the syllogism
Syllogism
A syllogism is a kind of logical argument in which one proposition is inferred from two or more others of a certain form...
- All dogs are mammals
- No mammal is a herbivore
- Thus, no dog is a herbivore
can be notated in the language of monadic predicate calculus as
where
 ,
,  and
and  denote the predicates of being, respectively, a dog, a mammal, and a herbivore.
denote the predicates of being, respectively, a dog, a mammal, and a herbivore.Conversely, monadic predicate calculus is not significantly more expressive than term logic. It is easily proved that every formula in the monadic predicate calculus is equivalent
Logical equivalence
In logic, statements p and q are logically equivalent if they have the same logical content.Syntactically, p and q are equivalent if each can be proved from the other...
to a formula in which quantifiers appear only in closed subformulae of the form

or
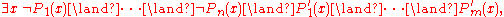
Each of these formulas is the negation of the other, and the quantifiers do not nest. These formulas also generalize slightly the form of basic judgements considered in term logic. For example, this form allows statements such as "Every mammal is either a herbivore or a carnivore (or both)",
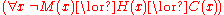 . Reasoning about such statements can, however, still be handled within the framework of term logic, although not by the 19 classical Aristotelian syllogism
. Reasoning about such statements can, however, still be handled within the framework of term logic, although not by the 19 classical Aristotelian syllogismSyllogism
A syllogism is a kind of logical argument in which one proposition is inferred from two or more others of a certain form...
s alone.
Taking propositional logic as given, every formula in the monadic predicate calculus expresses something that can likewise be formulated in term logic. On the other hand, a modern view of the problem of multiple generality
Problem of multiple generality
The problem of multiple generality names a failure in traditional logic to describe certain intuitively valid inferences. For example, it is intuitively clear that if:then it follows logically that:The syntax of traditional logic permits exactly four sentence types: "All As are Bs", "No As are...
in traditional logic concludes that quantifiers cannot nest usefully if there are no polyadic predicates to relate the bound variables.
Variants
The formal system describe in this entry is sometimes called the pure monadic predicate calculus, where "pure" signifies the absence of function letters. Allowing monadic function letters changes the logic only superficially, whereas admitting even a single binary function letter would result in a system with the expressive power of the full predicate calculus.Monadic predicate calculus is also called monadic first-order logic. Monadic second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
keeps the requirement that all predicates be unary, but allows for quantification over predicates as well as variables.