Variable (mathematics)
Encyclopedia
In mathematics
, a variable is a value
that may change within the scope of a given problem or set of operations. In contrast, a constant
is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and its applications
. A "constant" in this context should not be confused with a mathematical constant
which is a specific number independent of the scope of the given problem.
When one value is completely determined by another, or several others, then it is called a function
of the other value or values. In this case the value of the function is a dependent variable and the other values are independent variables. The notation f(x) is used for the value of the function f with x representing the independent variable. Similarly, notation such as f(x, y, z) may be used when there are several independent variables.
in which the variable occurs, as in the case of summation variables or variables that designate the argument of a function
being defined. The context can also be larger, for instance when a variable is used to designate a value occurring in a hypothesis of the discussion at hand. In some cases nothing varies at all, and alternative names can be used instead of "variable": a parameter is a value that is fixed in the statement of the problem being studied (although its value may not be explicitly known), an unknown is a variable that is introduced to stand for a constant value that is not initially known, but which may become known by solving some equation(s) for it, and an indeterminate is a symbol that need not stand for anything else but is an abstract value in itself. In all these cases the term "variable" is often still used because the rules for the manipulation of these symbols are the same; however, in some languages other than English, one distinguishes between "variables" in functions and "unknown quantities" in equations ("incógnita" in Portuguese/Spanish, "inconnue" in French).
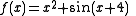
then x is a variable standing for the argument of the function being defined, which can be any real number. In the identity
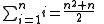
the variable i is a summation variable which designates in turn each of the integers 1, 2, ..., n (it is also called index because its variation is over a discrete set of values) while n is a parameter (it does not vary within the formula).
In the theory of polynomials, a polynomial of degree 2 is generally denoted as ax2 + bx + c, where a, b and c are called coefficient
s (they are assumed to be fixed, i.e., parameters of the problem considered) while x is called a variable. When studying this polynomial for its polynomial function this x stands for the function argument. When studying the polynomial as an object in itself, x is taken to be an indeterminate, and would often be written with a capital letter instead to indicate this status.
Formulas from physics
such as E = mc2 or PV = nRT (the ideal gas law
) do not involve the mathematical notion of a variable, because the quantities E, m, P, V, n, and T are instead used to designate certain properties (energy, mass, pressure, volume, quantity, temperature) of the physical system.
, variables and constants are usually set in an italic type
face.
Specific branches and applications of mathematics usually have specific naming convention
s for variables. Variables with similar roles or meanings are often assigned consecutive letters. For example, the three axes in 3D coordinate space
are conventionally called x, y, and z, while random variable
s in statistics are usually named X, Y, Z. In physics, the names of variables are largely determined by the physical quantity
they describe, but various naming conventions exist.
A convention sometimes followed in statistics
is to use X, Y, Z for the names of random variables, with these being replaced by x, y, z for observations or sample outcomes of those random variables. Another convention sometimes used in statistics is to denote population values of particular statistics by lower (or upper) case Greek letters, with sample-based estimates of those quantities being denoted by the corresponding lower (or upper) case letters from the ordinary alphabet.
s. For instance, in the formula x + 1 = 5, x is a variable which represents an "unknown" number
. Variables are often represented by Greek
or Roman letter
s and may be used with other special symbols.
In mathematics, variables are essential because they let quantitative relationships to be stated in a general way. If we were forced to use actual values, then the relationships would only apply in a more narrow set of situations. For example:
2(x) = x + x or x * 2
So in this example, the variable x is a "placeholder" for any number—that is to say, a variable. One important thing we assume is that the value of x does not change, even though we do not know what x is. But in some algorithms, obviously, will change x, and there are various ways to then denote if we mean its old or new value—again, generally not knowing either, but perhaps (for example) that one is less than the other.
, variables refer to measurable attributes, as these typically vary over time or between individuals. Variables can be discrete (taking values from a finite or countable set), continuous (having a continuous
distribution function
), or neither. Temperature is a continuous variable, while the number of legs of an animal is a discrete variable. This concept of a variable is widely used in the natural
, medical, and social sciences.
In causal models, a distinction is made between "independent variable
s" and "dependent variables", the latter being expected to vary in value in response to changes in the former. In other words, an independent variable is presumed to potentially affect a dependent one. In experiments, independent variables include factors that can be altered or chosen by the researcher independent of other factors.
So, in an experiment to test if the boiling point of water changes with altitude, the altitude is under direct control and is the independent variable, and the boiling point is presumed to depend upon it, so being the dependent variable. The results of an experiment, or information to be used to draw conclusions, are known as data
. It is often important to consider which variables to allow, or directly control or eliminate, in the design of experiments
.
There are also quasi-independent variables, which are used by researchers to group things without affecting the variable itself. For example, to separate people into groups by their sex does not change whether they are male or female. Or a researcher may separate people, arbitrarily, on the amount of coffee they had drunk before beginning an experiment. The researcher cannot change the past, but can use it to split people into groups.
While independent variables can refer to quantities and qualities that are under experimental control, they can also include extraneous factors that influence results in a confusing or undesired manner. In statistics the technique to work this out is called correlation
.
If strongly confounding variables exist that can substantially change the result, it makes it harder to interpret. For example, a study on cancer against age will also have to take into account variables such as income, location
, stress
, and lifestyle. Without considering these, the results could be grossly inaccurate deductions. Because of this, controlling unwanted variables is important in research.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a variable is a value
Value (mathematics)
In mathematics, value commonly refers to the 'output' of a function. In the most basic case, that of unary, single-valued functions, there is one input and one output .The function f of the example is real-valued, since each and every possible function value is real...
that may change within the scope of a given problem or set of operations. In contrast, a constant
Constant (mathematics)
In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition to variable In mathematics, a constant is a non-varying value, i.e. completely fixed or fixed in the context of use. The term usually occurs in opposition...
is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and its applications
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
. A "constant" in this context should not be confused with a mathematical constant
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
which is a specific number independent of the scope of the given problem.
Dependent and independent variables
Variables are further distinguished as being either a dependent variable or an independent variable. Independent variables are regarded as inputs to a system and may take on different values freely. Dependent variables are those values that change as a consequence of changes in other values in the system.When one value is completely determined by another, or several others, then it is called a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of the other value or values. In this case the value of the function is a dependent variable and the other values are independent variables. The notation f(x) is used for the value of the function f with x representing the independent variable. Similarly, notation such as f(x, y, z) may be used when there are several independent variables.
What it means for a variable to vary
Varying, in the context of mathematical variables, does not mean change in the course of time, but rather dependence on the context in which the variable is used. This can be the immediate context of the expressionExpression (mathematics)
In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
in which the variable occurs, as in the case of summation variables or variables that designate the argument of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
being defined. The context can also be larger, for instance when a variable is used to designate a value occurring in a hypothesis of the discussion at hand. In some cases nothing varies at all, and alternative names can be used instead of "variable": a parameter is a value that is fixed in the statement of the problem being studied (although its value may not be explicitly known), an unknown is a variable that is introduced to stand for a constant value that is not initially known, but which may become known by solving some equation(s) for it, and an indeterminate is a symbol that need not stand for anything else but is an abstract value in itself. In all these cases the term "variable" is often still used because the rules for the manipulation of these symbols are the same; however, in some languages other than English, one distinguishes between "variables" in functions and "unknown quantities" in equations ("incógnita" in Portuguese/Spanish, "inconnue" in French).
Examples
If one defines a function f from the real numbers to the real numbers by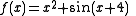then x is a variable standing for the argument of the function being defined, which can be any real number. In the identity
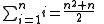
the variable i is a summation variable which designates in turn each of the integers 1, 2, ..., n (it is also called index because its variation is over a discrete set of values) while n is a parameter (it does not vary within the formula).
In the theory of polynomials, a polynomial of degree 2 is generally denoted as ax2 + bx + c, where a, b and c are called coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s (they are assumed to be fixed, i.e., parameters of the problem considered) while x is called a variable. When studying this polynomial for its polynomial function this x stands for the function argument. When studying the polynomial as an object in itself, x is taken to be an indeterminate, and would often be written with a capital letter instead to indicate this status.
Formulas from physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
such as E = mc2 or PV = nRT (the ideal gas law
Ideal gas law
The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...
) do not involve the mathematical notion of a variable, because the quantities E, m, P, V, n, and T are instead used to designate certain properties (energy, mass, pressure, volume, quantity, temperature) of the physical system.
Notation
In mathematics, single-symbol names for variables are the norm, with letter at the beginning of the alphabet, e.g. a, b, c commonly used for constants and letters at the end of the alphabet, e.g. x, y, z, and t commonly used for variables. In written mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, variables and constants are usually set in an italic type
Italic type
In typography, italic type is a cursive typeface based on a stylized form of calligraphic handwriting. Owing to the influence from calligraphy, such typefaces often slant slightly to the right. Different glyph shapes from roman type are also usually used—another influence from calligraphy...
face.
Specific branches and applications of mathematics usually have specific naming convention
Naming convention
A naming convention is a convention for naming things. The intent is to allow useful information to be deduced from the names based on regularities. For instance, in Manhattan, streets are numbered, with East-West streets being called "Streets" and North-South streets called "Avenues".-Use...
s for variables. Variables with similar roles or meanings are often assigned consecutive letters. For example, the three axes in 3D coordinate space
Coordinate space
In mathematics, specifically in linear algebra, the coordinate space, Fn, is the prototypical example of an n-dimensional vector space over a field F. It can be defined as the product space of F over a finite index set.-Definition:...
are conventionally called x, y, and z, while random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s in statistics are usually named X, Y, Z. In physics, the names of variables are largely determined by the physical quantity
Physical quantity
A physical quantity is a physical property of a phenomenon, body, or substance, that can be quantified by measurement.-Definition of a physical quantity:Formally, the International Vocabulary of Metrology, 3rd edition defines quantity as:...
they describe, but various naming conventions exist.
A convention sometimes followed in statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
is to use X, Y, Z for the names of random variables, with these being replaced by x, y, z for observations or sample outcomes of those random variables. Another convention sometimes used in statistics is to denote population values of particular statistics by lower (or upper) case Greek letters, with sample-based estimates of those quantities being denoted by the corresponding lower (or upper) case letters from the ordinary alphabet.
General introduction
Variables are used in open sentenceOpen sentence
In mathematics, an open sentence is described as "open" in the sense that its truth value is meaningless until its variables are replaced with specific numbers, at which point the truth value can usually be determined...
s. For instance, in the formula x + 1 = 5, x is a variable which represents an "unknown" number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
. Variables are often represented by Greek
Greek alphabet
The Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
or Roman letter
Letter (alphabet)
A letter is a grapheme in an alphabetic system of writing, such as the Greek alphabet and its descendants. Letters compose phonemes and each phoneme represents a phone in the spoken form of the language....
s and may be used with other special symbols.
In mathematics, variables are essential because they let quantitative relationships to be stated in a general way. If we were forced to use actual values, then the relationships would only apply in a more narrow set of situations. For example:
-
- State a mathematical definition for finding the number twice that of ANY other finite number:
2(x) = x + x or x * 2
-
- Now, all we need to do to find the double of a number is replace x with any number we want.
-
-
- 2(1) = 1 + 1 = 2 or 1 * 2
- 2(3) = 3 + 3 = 6 or 3 * 2
- 2(55) = 55 + 55 = 110 or 55 * 2
- etc.
-
So in this example, the variable x is a "placeholder" for any number—that is to say, a variable. One important thing we assume is that the value of x does not change, even though we do not know what x is. But in some algorithms, obviously, will change x, and there are various ways to then denote if we mean its old or new value—again, generally not knowing either, but perhaps (for example) that one is less than the other.
Naming conventions
Mathematics has many conventions. Below are some of the more common. Many of the symbols have other conventional uses, but they may actually represent a constant or a specific function rather than a variable.- ai is often used to denote a term of a sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
. - a, b, c, and d (sometimes extended to e and f) usually play similar roles or are made to represent parallel notions in a mathematical context. They often represent constants.
- The coefficients in an equation, for example the general expression of a polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
or a Diophantine equationDiophantine equationIn mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
are often a, b, c, d, e, and f.
- The coefficients in an equation, for example the general expression of a polynomial
- f and g (sometimes h) commonly denote functionsFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. - i, j, and k (sometimes l or h) are often used as subscripts to denote indicesIndex (mathematics)The word index is used in variety of senses in mathematics.- General :* In perhaps the most frequent sense, an index is a number or other symbol that indicates the location of a variable in a list or array of numbers or other mathematical objects. This type of index is usually written as a...
. - l and w are often used to represent the length and width of a figure.
- m and n usually denote integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s and usually play similar roles or are made to represent parallel notions in a mathematical context, such a pair of dimensions.- n commonly denotes a count of objects, or, in statistics, the number of individuals or observations.
- p, q, and r usually play similar roles or are made to represent parallel notions in a mathematical context.
- p and q often denote prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s or relatively prime numbers, or, in statistics, probabilities.
- p and q often denote prime number
- r often denotes a remainder or modulus.
- r, s, and t usually play similar roles or are made to represent parallel notions in a mathematical context.
- u and v usually play similar roles or are made to represent parallel notions in a mathematical context, such as denoting a vertex (graph theory)Vertex (graph theory)In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
. - w, x, y, and z usually play similar roles or are made to represent parallel notions in a mathematical context, such as representing unknowns in an equation.
- x, y and z correspond to the three Cartesian axes. In many two-dimensional cases, y will be expressed in terms of x; if a third dimension is added, z is expressed in terms of x and y.
- z typically denotes a complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, or, in statistics, a normal random variate.
- z typically denotes a complex number
-
, 
, 
, 
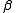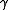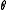and 
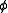commonly denote angleAngleIn geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
measures. -
usually represents an arbitrarily small positive number.
-
and 
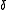commonly denote two small positives.
-
-
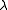is used for eigenvalues. -
often denotes a sum, or, in statistics, the standard deviationStandard deviationStandard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
.
Applied statistics
In statisticsStatistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, variables refer to measurable attributes, as these typically vary over time or between individuals. Variables can be discrete (taking values from a finite or countable set), continuous (having a continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
), or neither. Temperature is a continuous variable, while the number of legs of an animal is a discrete variable. This concept of a variable is widely used in the natural
Natural science
The natural sciences are branches of science that seek to elucidate the rules that govern the natural world by using empirical and scientific methods...
, medical, and social sciences.
In causal models, a distinction is made between "independent variable
Independent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
s" and "dependent variables", the latter being expected to vary in value in response to changes in the former. In other words, an independent variable is presumed to potentially affect a dependent one. In experiments, independent variables include factors that can be altered or chosen by the researcher independent of other factors.
So, in an experiment to test if the boiling point of water changes with altitude, the altitude is under direct control and is the independent variable, and the boiling point is presumed to depend upon it, so being the dependent variable. The results of an experiment, or information to be used to draw conclusions, are known as data
Data
The term data refers to qualitative or quantitative attributes of a variable or set of variables. Data are typically the results of measurements and can be the basis of graphs, images, or observations of a set of variables. Data are often viewed as the lowest level of abstraction from which...
. It is often important to consider which variables to allow, or directly control or eliminate, in the design of experiments
Design of experiments
In general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. However, in statistics, these terms are usually used for controlled experiments...
.
There are also quasi-independent variables, which are used by researchers to group things without affecting the variable itself. For example, to separate people into groups by their sex does not change whether they are male or female. Or a researcher may separate people, arbitrarily, on the amount of coffee they had drunk before beginning an experiment. The researcher cannot change the past, but can use it to split people into groups.
While independent variables can refer to quantities and qualities that are under experimental control, they can also include extraneous factors that influence results in a confusing or undesired manner. In statistics the technique to work this out is called correlation
Correlation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
.
If strongly confounding variables exist that can substantially change the result, it makes it harder to interpret. For example, a study on cancer against age will also have to take into account variables such as income, location
Location (geography)
The terms location and place in geography are used to identify a point or an area on the Earth's surface or elsewhere. The term 'location' generally implies a higher degree of can certainty than "place" which often has an ambiguous boundary relying more on human/social attributes of place identity...
, stress
Stress (medicine)
Stress is a term in psychology and biology, borrowed from physics and engineering and first used in the biological context in the 1930s, which has in more recent decades become commonly used in popular parlance...
, and lifestyle. Without considering these, the results could be grossly inaccurate deductions. Because of this, controlling unwanted variables is important in research.
See also
- Bound variable, also known as a dummy variable
- Free variables and bound variablesFree variables and bound variablesIn mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a free variable is a notation that specifies places in an expression where substitution may take place...
- Variable (programming)Variable (programming)In computer programming, a variable is a symbolic name given to some known or unknown quantity or information, for the purpose of allowing the name to be used independently of the information it represents...
- Mathematical expressionExpression (mathematics)In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
- Physical constantPhysical constantA physical constant is a physical quantity that is generally believed to be both universal in nature and constant in time. It can be contrasted with a mathematical constant, which is a fixed numerical value but does not directly involve any physical measurement.There are many physical constants in...
- CoefficientCoefficientIn mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
- Constant of integration
- Constant term of a polynomialConstant termIn mathematics, a constant term is a term in an algebraic expression has a value that is constant or cannot change, because it does not contain any modifiable variables. For example, in the quadratic polynomialx^2 + 2x + 3,\ the 3 is a constant term....
- Indeterminate (variable)Indeterminate (variable)In mathematics, and particularly in formal algebra, an indeterminate is a symbol that does not stand for anything else but itself. In particular it does not designate a constant, or a parameter of the problem, it is not an unknown that could be solved for, it is not a variable designating a...