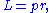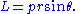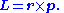Physical quantity
Encyclopedia
A physical quantity is a physical property
of a phenomenon
, body, or substance, that can be quantified
by measurement
.
Hence the value of a physical quantity q is expressed as the product
of a numerical value
Nq and a unit of measurement uq;
Quantity calculus
describes how to do maths with quantities.
Examples
In practice, note that different observers may get different values of a quantity depending on the frame of reference; in turn the coordinate system and metric. Physical properties such as length, mass or time, by themselves, are not physically invariant. However, the laws of physics which include these properties are invariant.
Intensive quantity: the magnitude is independent of the extent of the system (temperature, pressure, etc.)
There are also physical quantities that can be classified as neither extensive nor intensive, for example angular momentum
, area
, force
, length
, and time
.
. For example, the recommended symbol for the physical quantity 'mass' is m, and the recommended symbol for the quantity 'charge' is Q.
Subscripts and indices
Subscripts are used for two reasons, to simply attach a name to the quantity or associate it with another quantity, or represent a specific vector, matrix, or tensor component.
Scalars: Symbol
s for physical quantities are usually chosen to be a single letter of the Latin
or Greek alphabet
, and are printed in italic type.
Vectors: Symbols for physical quantities that are vectors are in bold type, underlined or with an arrow above. If, e.g., u is the speed of a particle, then the straightforward notation for its velocity is u, u, or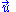
.
Numbers and elementary functions
Numerical quantities, even those denoted by letters, are usually printed in roman (upright) type, though sometimes can be italic. Symbols for elementary functions (circular trigonometric, hyperbolic, logarithmic etc.), changes in a quantity like Δ in Δy or operators like d in dx, are also recommended to be printed in roman type.
Most physical quantities include a unit, but not all - some are dimensionless. Neither the name of a physical quantity, nor the symbol used to denote it, implies a particular choice of unit, though SI
units
are usually preferred and assumed today due to their ease of use and all-round applicability. For example, a quantity of mass might be represented by the symbol m, and could be expressed in the units kilogram
s (kg), pounds
(lb), or Daltons
(Da).
Dimensions
The notion of physical dimension
of a physical quantity was introduced by Joseph Fourier
in 1822. By convention, physical quantities are organized in a dimensional system built upon base quantities, each of which is regarded as having its own dimension.
units and dimensions are listed in the following table. Other conventions may have a different number of fundamental units (e.g. the CGS and MKS
systems of units).
The last two angular units; plane angle and solid angle
are subsidiary units used in the SI, but treated dimensionless. The subsidiary units are used for convenience to differentiate between a truly dimensionless quantity (pure number) and an angle, which are different measurements.
Colour mixing analogy
Defining quantities is analogous to mixing colours, and could be classified a similar way, although this is not standard. Primary colours are to base quantities; as secondary (or tertiary etc.) colours are to derived quantities. Mixing colours is analogous to combining quantities using mathematical operations. But colours could be for light
or paint
, and analogously the system of units could be one of many forms: such as SI (now most common), CGS
, Gaussian
, old imperial units, a specific form of natural units
or even arbitrarily defined units characteristic to the physical system in consideration (characteristic units
).
The choice of a base system of quantities and units is arbitrary; but once chosen it must be adhered to throughout all analysis which follows for consistency. It makes no sense to mix up different systems of units. Choosing a system of units, one system out of the SI, CGS etc., is like choosing whether use paint or light colours.
In light of this analogy, primary definitions are base quantities with no defining equation, but defined standardized condition, "secondary" definitions are quantities defined purely in terms of base quantities, "tertiary" for quantities in terms of both base and "secondary" quantities, "quaternary" for quantities in terms of base, "secondary", and "tertiary" quantities, and so on.
Theoretical implications: Definitions are important since they can lead into new insights of a branch of physics. Two such examples occurred in classical physics. When entropy
S was defined – the range of thermodynamics
was greatly extended by associating chaos and disorder
with a numerical quantity that could relate to energy and temperature, leading to the understanding of the second
thermodynamic law
and statistical mechanics
. Also the action
functional
(also written S) (together with generalized coordinates
and momenta
and the lagrangian
function), initially an alternative formulation of classical mechanics
to Newton's laws, now extends the range of modern physics in general – notably quantum mechanics
and particle physics
.
Analytical convenience: They allow other equations to be written more compactly and so allow easier mathematical manipulation; by including a parameter in a definition, occurrences of the parameter can be absorbed into the substituted quantity and removed from the equation.
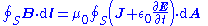
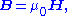
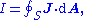
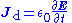leading to the displacement current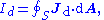 
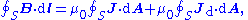
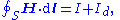
Ease of comparison: They allow comparisons of measurements to be made when they might appear ambiguous and unclear otherwise.
and calculus
, vector algebra and calculus, or for the most general applications tensor algebra and calculus
, depending on the level of study and presentation, complexity of topic and scope of applicability. Functions may be incorporated into a definition, in for calculus this is necessary. Quantities may also be complex
-valued for theoretical advantage, but for a physical measurement the real part is relevant, the imaginary part can be discarded. For more advanced treatments the equation may have to be written in an equivalent but alternative form using other defining equations for the definition to be useful. Often definitions can start from elementary algebra, then modify to vectors, then in the limiting cases calculus may be used. The various levels of maths used typically follows this pattern.
Typically definitions are explicit, meaning the defining quantity is the subject of the equation, but sometimes the equation is not written explicitly – although the defining quantity can be solved for to make the equation explicit. For vector equations, sometimes the defining quantity is in a cross or dot product and cannot be solved for explicitly as a vector, but the components can.
Physical property
A physical property is any property that is measurable whose value describes a physical system's state. The changes in the physical properties of a system can be used to describe its transformations ....
of a phenomenon
Phenomenon
A phenomenon , plural phenomena, is any observable occurrence. Phenomena are often, but not always, understood as 'appearances' or 'experiences'...
, body, or substance, that can be quantified
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
by measurement
Measurement
Measurement is the process or the result of determining the ratio of a physical quantity, such as a length, time, temperature etc., to a unit of measurement, such as the metre, second or degree Celsius...
.
Definition of a physical quantity
Formally, the International Vocabulary of Metrology, 3rd edition (VIM3) defines quantity as:Hence the value of a physical quantity q is expressed as the product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
of a numerical value
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
Nq and a unit of measurement uq;
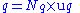
Quantity calculus
Quantity calculus
Quantity calculus is the formal method for describing the mathematical relations between abstract physical quantities. Despite the name, it is more analogous to a system of algebra than calculus in the mathematical sense of the term. Measurements are expressed as products of a numeric value with a...
describes how to do maths with quantities.
Examples
- If the temperature T of a body is quantified as 300 kelvin (in which T is the quantity symbol, 300 the value, and K is the unit), this is written
- T = 300 × K = 300 K,
- If a person weighs 120 poundsPound (mass)The pound or pound-mass is a unit of mass used in the Imperial, United States customary and other systems of measurement...
, then "120" is the numerical value and "pound" is the unit. This physical quantity mass would be written as "120 lb", or
- m = 120 lb
- If a person traveling with a yardstick, measures the length of such yardstick, the physical quantity of length would be written as
- L = 36 inches
- An example employing SISiSi, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units and scientific notationScientific notationScientific notation is a way of writing numbers that are too large or too small to be conveniently written in standard decimal notation. Scientific notation has a number of useful properties and is commonly used in calculators and by scientists, mathematicians, doctors, and engineers.In scientific...
for the number, might be a measurement of powerPower (physics)In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
written as
- P = 42.3 × 103 W,
In practice, note that different observers may get different values of a quantity depending on the frame of reference; in turn the coordinate system and metric. Physical properties such as length, mass or time, by themselves, are not physically invariant. However, the laws of physics which include these properties are invariant.
Extensive and intensive quantities
Extensive quantity: its magnitude is additive for subsystems (volume, mass, etc.)Intensive quantity: the magnitude is independent of the extent of the system (temperature, pressure, etc.)
There are also physical quantities that can be classified as neither extensive nor intensive, for example angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
, area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
, force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
, length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
, and time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
.
Symbols, nomenclature
General: Symbols for quantities should be chosen according to the international recommendations from ISO 80000, the IUPAP red book and the IUPAC green bookIUPAC green book
right|thumb|Front cover of the Green BookQuantities, Units and Symbols in Physical Chemistry Third Edition , also known as the Green Book, published in Aug 2007 by IUPAC is based on the most up to date sources for fundamental constants, data and nomenclature in the field of chemistry and physics...
. For example, the recommended symbol for the physical quantity 'mass' is m, and the recommended symbol for the quantity 'charge' is Q.
Subscripts and indices
Subscripts are used for two reasons, to simply attach a name to the quantity or associate it with another quantity, or represent a specific vector, matrix, or tensor component.
- Name reference: The quantity has a subscripted or superscripted single letter, a number of letters, or an entire word, to specify what concept or entity they refer to, and tend to be written in upright roman typeface rather than italic while the quantity is in italic. For instance Ek or Ekinetic is usually used to denote kinetic energyKinetic energyThe kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
and Ep or Epotential is usually used to denote potential energyPotential energyIn physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
.
- Quantity reference: The quantity has a subscripted or superscripted single letter, a number of letters, or an entire word, to specify what measurement/s they refer to, and tend to be written in italic rather than upright roman typeface while the quantity is also in italic. For example cp or cisobaric is heat capacityHeat capacityHeat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
at constant pressurePressurePressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
.
- Note the difference in the style of the subscripts: k and p are abbreviations of the words kinetic and potential, whereas p (italic) is the symbol for the physical quantity pressure rather than an abbreviation of the word "pressure".
- Indices: These are quite apart from the above, their use is for mathematical formalism, see Index notationIndex notationIndex notation is used in mathematics and computer programming to specify the elements of matrices or the components of a vector. The formalism of how indices are used varies according to the discipline...
.
Scalars: Symbol
Symbol
A symbol is something which represents an idea, a physical entity or a process but is distinct from it. The purpose of a symbol is to communicate meaning. For example, a red octagon may be a symbol for "STOP". On a map, a picture of a tent might represent a campsite. Numerals are symbols for...
s for physical quantities are usually chosen to be a single letter of the Latin
Latin alphabet
The Latin alphabet, also called the Roman alphabet, is the most recognized alphabet used in the world today. It evolved from a western variety of the Greek alphabet called the Cumaean alphabet, which was adopted and modified by the Etruscans who ruled early Rome...
or Greek alphabet
Greek alphabet
The Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
, and are printed in italic type.
Vectors: Symbols for physical quantities that are vectors are in bold type, underlined or with an arrow above. If, e.g., u is the speed of a particle, then the straightforward notation for its velocity is u, u, or
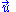.Numbers and elementary functions
Numerical quantities, even those denoted by letters, are usually printed in roman (upright) type, though sometimes can be italic. Symbols for elementary functions (circular trigonometric, hyperbolic, logarithmic etc.), changes in a quantity like Δ in Δy or operators like d in dx, are also recommended to be printed in roman type.
- Examples
- real numbers are as usual, such as 1 or √2,
- e for the base of natural logarithm,
- i for the imaginary unit,
- π for 3.14152658...
- δx, Δy, dz,
- sin α, sinh γ, log x
Units and dimensions
UnitsMost physical quantities include a unit, but not all - some are dimensionless. Neither the name of a physical quantity, nor the symbol used to denote it, implies a particular choice of unit, though SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units
Units of measurement
A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of...
are usually preferred and assumed today due to their ease of use and all-round applicability. For example, a quantity of mass might be represented by the symbol m, and could be expressed in the units kilogram
Kilogram
The kilogram or kilogramme , also known as the kilo, is the base unit of mass in the International System of Units and is defined as being equal to the mass of the International Prototype Kilogram , which is almost exactly equal to the mass of one liter of water...
s (kg), pounds
Pound (mass)
The pound or pound-mass is a unit of mass used in the Imperial, United States customary and other systems of measurement...
(lb), or Daltons
Atomic mass unit
The unified atomic mass unit or dalton is a unit that is used for indicating mass on an atomic or molecular scale. It is defined as one twelfth of the rest mass of an unbound neutral atom of carbon-12 in its nuclear and electronic ground state, and has a value of...
(Da).
Dimensions
The notion of physical dimension
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
of a physical quantity was introduced by Joseph Fourier
Joseph Fourier
Jean Baptiste Joseph Fourier was a French mathematician and physicist best known for initiating the investigation of Fourier series and their applications to problems of heat transfer and vibrations. The Fourier transform and Fourier's Law are also named in his honour...
in 1822. By convention, physical quantities are organized in a dimensional system built upon base quantities, each of which is regarded as having its own dimension.
Base quantities
The seven base quantities of the International System of Quantities (ISQ) and their corresponding SISi
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units and dimensions are listed in the following table. Other conventions may have a different number of fundamental units (e.g. the CGS and MKS
Mks system of units
The MKS system of units is a physical system of units that expresses any given measurement using fundamental units of the metre, kilogram, and/or second ....
systems of units).
| Quantity name/s | (Common) Quantity symbol/s | SI unit name | SI unit symbol | Dimension symbol |
|---|---|---|---|---|
| Length Length In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire... , width, height, depth |
a, b, c, d, h, l, r, w, x, y, z | metre Metre The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology... |
m | [L] |
| Time Time Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects.... |
t | second Second The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock.... |
s | [T] |
| Mass Mass Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:... |
m | kilogram Kilogram The kilogram or kilogramme , also known as the kilo, is the base unit of mass in the International System of Units and is defined as being equal to the mass of the International Prototype Kilogram , which is almost exactly equal to the mass of one liter of water... |
kg | [M] |
| Temperature Temperature Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot... |
T, θ | kelvin Kelvin The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all... |
K | [Θ] |
| Amount of substance Matter Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume... , number of moles |
n | mole Mole (unit) The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value... |
mol | [N] |
| Electric current Electric current Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire... |
i, I | ampere Ampere The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics... |
A | [I] |
| Luminous intensity Luminous intensity In photometry, luminous intensity is a measure of the wavelength-weighted power emitted by a light source in a particular direction per unit solid angle, based on the luminosity function, a standardized model of the sensitivity of the human eye... |
Iv | candela Candela The candela is the SI base unit of luminous intensity; that is, power emitted by a light source in a particular direction, weighted by the luminosity function . A common candle emits light with a luminous intensity of roughly one candela... |
Cd | [J] |
| Plane angle Angle In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc... |
α, β, γ, θ, φ, χ | radian Radian Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit... |
rad | dimensionless |
| Solid angle Solid angle The solid angle, Ω, is the two-dimensional angle in three-dimensional space that an object subtends at a point. It is a measure of how large that object appears to an observer looking from that point... |
ω, Ω | steradian Steradian The steradian is the SI unit of solid angle. It is used to describe two-dimensional angular spans in three-dimensional space, analogous to the way in which the radian describes angles in a plane... |
sr | dimensionless |
The last two angular units; plane angle and solid angle
Solid angle
The solid angle, Ω, is the two-dimensional angle in three-dimensional space that an object subtends at a point. It is a measure of how large that object appears to an observer looking from that point...
are subsidiary units used in the SI, but treated dimensionless. The subsidiary units are used for convenience to differentiate between a truly dimensionless quantity (pure number) and an angle, which are different measurements.
Physical quantities defined from equations
Description of units and physical quantities
Physical quantities and units follow the same hierarchy; chosen base quantities have defined base units, from these any other quantities may be derived and have corresponding derived units.Colour mixing analogy
Defining quantities is analogous to mixing colours, and could be classified a similar way, although this is not standard. Primary colours are to base quantities; as secondary (or tertiary etc.) colours are to derived quantities. Mixing colours is analogous to combining quantities using mathematical operations. But colours could be for light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
or paint
Paint
Paint is any liquid, liquefiable, or mastic composition which after application to a substrate in a thin layer is converted to an opaque solid film. One may also consider the digital mimicry thereof...
, and analogously the system of units could be one of many forms: such as SI (now most common), CGS
Centimetre gram second system of units
The centimetre–gram–second system is a metric system of physical units based on centimetre as the unit of length, gram as a unit of mass, and second as a unit of time...
, Gaussian
Gaussian units
Gaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
, old imperial units, a specific form of natural units
Natural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
or even arbitrarily defined units characteristic to the physical system in consideration (characteristic units
Nondimensionalization
Nondimensionalization is the partial or full removal of units from an equation involving physical quantities by a suitable substitution of variables. This technique can simplify and parameterize problems where measured units are involved. It is closely related to dimensional analysis...
).
The choice of a base system of quantities and units is arbitrary; but once chosen it must be adhered to throughout all analysis which follows for consistency. It makes no sense to mix up different systems of units. Choosing a system of units, one system out of the SI, CGS etc., is like choosing whether use paint or light colours.
In light of this analogy, primary definitions are base quantities with no defining equation, but defined standardized condition, "secondary" definitions are quantities defined purely in terms of base quantities, "tertiary" for quantities in terms of both base and "secondary" quantities, "quaternary" for quantities in terms of base, "secondary", and "tertiary" quantities, and so on.
Motivation
Much of physics requires definitions to be made for the equations to make sense.Theoretical implications: Definitions are important since they can lead into new insights of a branch of physics. Two such examples occurred in classical physics. When entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
S was defined – the range of thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
was greatly extended by associating chaos and disorder
Order and disorder (physics)
In physics, the terms order and disorder designate the presence or absence of some symmetry or correlation in a many-particle system.In condensed matter physics, systems typically are ordered at low temperatures; upon heating, they undergo one or several phase transitions into less ordered...
with a numerical quantity that could relate to energy and temperature, leading to the understanding of the second
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
thermodynamic law
Laws of thermodynamics
The four laws of thermodynamics summarize its most important facts. They define fundamental physical quantities, such as temperature, energy, and entropy, in order to describe thermodynamic systems. They also describe the transfer of energy as heat and work in thermodynamic processes...
and statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. Also the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
(also written S) (together with generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
and momenta
Canonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
and the lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
function), initially an alternative formulation of classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
to Newton's laws, now extends the range of modern physics in general – notably quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
.
Analytical convenience: They allow other equations to be written more compactly and so allow easier mathematical manipulation; by including a parameter in a definition, occurrences of the parameter can be absorbed into the substituted quantity and removed from the equation.
- Example
- As an example consider Ampère's circuital law (with Maxwell's correction) in integral form for an arbitrary current carrying conductorElectrical conductorIn physics and electrical engineering, a conductor is a material which contains movable electric charges. In metallic conductors such as copper or aluminum, the movable charged particles are electrons...
in a vacuumVacuumIn everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
(so zero magnetizationMagnetizationIn classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
due medium, i.e M = 0):
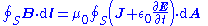
- using the constitutive definition
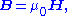
- and the current density definition
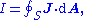
- similarly for the displacement currentDisplacement currentIn electromagnetism, displacement current is a quantity that is defined in terms of the rate of change of electric displacement field. Displacement current has the units of electric current density, and it has an associated magnetic field just as actual currents do. However it is not an electric...
density
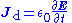leading to the displacement current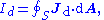 - we have
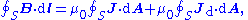
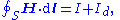
- which is simpler to write, even if the equation is the same.
Ease of comparison: They allow comparisons of measurements to be made when they might appear ambiguous and unclear otherwise.
- Example
- A basic example is mass density. It is not clear how compare how much matter constitutes a variety of substances given only their masses or only their volumes. Given both for each substance, the mass m per unit volume V, or mass density ρ provides a meaningful comparison between the substances, since for each, a fixed amount of volume will correspond to an amount of mass depending on the substance. To illustrate this; if two substances A and B have masses mA and mB respectively, occupying volumes VA and VB respectively, using the definition of mass density gives:
- ρA = mA / VA , ρB = mB / VB
- following this can be seen that:
- if mA > mB or mA < mB and VA = VB, then ρA > ρB or ρA < ρB,
- if mA = mB and VA > VB or VA < VB, then ρA < ρB or ρA > ρB,
- if ρA = ρB, then ρA > ρB, then mA / VA = mB / VB so mA / mB = VA / VB, demonstrating that if mA > mB or mA < mB, then VA > VB or VA < VB.
Scope of defining equations
Defining equations are normally formulated in terms of elementary algebraElementary algebra
Elementary algebra is a fundamental and relatively basic form of algebra taught to students who are presumed to have little or no formal knowledge of mathematics beyond arithmetic. It is typically taught in secondary school under the term algebra. The major difference between algebra and...
and calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, vector algebra and calculus, or for the most general applications tensor algebra and calculus
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
, depending on the level of study and presentation, complexity of topic and scope of applicability. Functions may be incorporated into a definition, in for calculus this is necessary. Quantities may also be complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued for theoretical advantage, but for a physical measurement the real part is relevant, the imaginary part can be discarded. For more advanced treatments the equation may have to be written in an equivalent but alternative form using other defining equations for the definition to be useful. Often definitions can start from elementary algebra, then modify to vectors, then in the limiting cases calculus may be used. The various levels of maths used typically follows this pattern.
Typically definitions are explicit, meaning the defining quantity is the subject of the equation, but sometimes the equation is not written explicitly – although the defining quantity can be solved for to make the equation explicit. For vector equations, sometimes the defining quantity is in a cross or dot product and cannot be solved for explicitly as a vector, but the components can.
- Examples
- Electric current density is an example spanning all of these methods, Angular momentumAngular momentumIn physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
is an example which doesn't require calculus. See the classical mechanics section below for nomenclature and diagrams to the right.
- Elementary algebra
- Operations are simply multiplication and division. Equations may be written in a product or quotient form, both of course equivalent.
| Angular momentum | Electric current density | |
|---|---|---|
| Quotient form |  |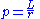
 |
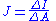| Product form |  |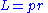
 |
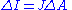- Vector algebra
- There is no way to divide a vector by a vector, so there are no product or quotient forms.
| Angular momentum | Electric current density | |
|---|---|---|
| Quotient form | N/A |  |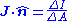
| Product form |   |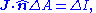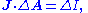
|
- Elementary calculus
- The arithmetic operations are modified to the limiting cases of differentiation and integration. Equations can be expressed in these equivalent and alternative ways.
| Current density | |
|---|---|
| Differential form |  |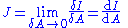
| Integral form | 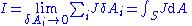 Alternatively for integral form   |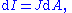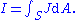
- Vector calculus
| Current density | |
|---|---|
| Differential form |  |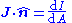
| Integral form |  |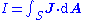
- Tensor analysis
- Vectors are rank-1 tensors. The formulae below are no more than the vector equations in the language of tensors.
Angular momentum Electric current density Differential form N/A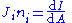 
Product/integral form Starting from
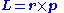
the components are Li, rj, pi, where i, j, k are each dummy indices each taking values 1, 2, 3, using the identity from tensor analysis
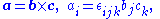
where εijk is the permutation/Levi-Cita tensorLevi-Civita symbolThe Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
, leads to
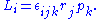
Using the Einstein summation convention,
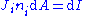
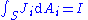
Multiple choice definitions
Sometimes there is still freedom within the chosen units system, to define one or more quantities in more than one way. The situation splits into two cases:
- Mutually exclusive definitions: There are a number of possible choices for a quantity to be defined in terms of others, but only one can be used and not the others. Choosing more than one of the exclusive equations for a definition leads to a contradiction – one equation might demand a quantity X to be defined in one way using another quantity Y, while another equation requires the reverse, Y be defined using X, but then another equation might falsify the use of both X and Y, and so on. The mutual disagreement makes it impossible to say which equation defines what quantity.
- Equivalent definitions: Defining equations which are equivalent and self-consistent with other equations and laws within the physical theory, simply written in different ways.
There are two possibilities for each case:
- One defining equation – one defined quantity: A defining equation is used to define a single quantity in terms of a number of others.
- One defining equation – a number of defined quantities: A defining equation is used to define a number of quantities in terms of a number of others. A single defining equation shouldn't contain one quantity defining all other quantities in the same equation, otherwise contradictions arise again. There is no definition of the defined quantities separately since they are defined by a single quantity in a single equation. Furthermore the defined quantities may have already been defined before, so if another quantity defines these in the same equation, there is a clash between definitions.
Contradictions can be avoided by defining quantities successively; the order in which quantities are defined must be accounted for. Examples spanning these instances occur in electromagnetismElectromagnetismElectromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, and are given below.
- Examples
- Mutually exclusive definitions:
- The magnetic induction fieldMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
B can be defined in terms of electric chargeElectric chargeElectric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
q or currentElectric currentElectric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
I, and the Lorentz forceLorentz forceIn physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
(magnetic term) F experienced by the charge carriers due to the field,
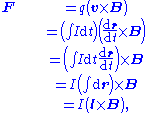
- where
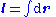is the change in position traversed by the charge carriers (assuming current is independent of position, if not so a line integral must be done along the path of current) or in terms of the magnetic flux ΦB through a surface S, where the area is used as a scalar A and vector: 
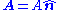and 
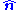is a unit normal to A, either in differential form
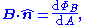
- or integral form,
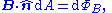
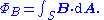
- However, only one of the above equations can be used to define B for the following reason, given that A, r, v, and F have been defined elsewhere unambiguously (most likely mechanics and Euclidean geometryEuclidean geometryEuclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
).
- If the force equation defines B, where q or I have been previously defined, then the flux equation defines ΦB, since B has been previously defined unambiguously. If the flux equation defines B, where ΦB, the force equation may be a defining equation for I or q. Notice the contradiction when B both equations define B simultaneously and when B is not a base quantity; the force equation demands that q or I be defined elsewhere while at the same time the flux equation demands that q or I be defined by the force equation, similarly the force equation requires ΦB to be defined by the flux equation, at the same time the flux equation demands that ΦB is defined elsewhere. For both equations to be used as definitions simultaneously, B must be a base quantity so that F and ΦB can be defined to stem from B unambiguously.
- Equivalent definitions:
- Another example is inductanceInductanceIn electromagnetism and electronics, inductance is the ability of an inductor to store energy in a magnetic field. Inductors generate an opposing voltage proportional to the rate of change in current in a circuit...
L which has two equivalent equations to use as a definition (see the defined quantity tables of electromagnetism section).
- In terms of I and ΦB, the inductance is given by
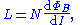
- in terms of I and induced emf V
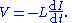
- These two are equivalent by Faraday's law of inductionFaraday's law of inductionFaraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
:
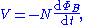
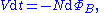
- substituting into the first definition for L
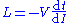
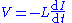
- and so they are not mutually exclusive.
- One defining equation – a number of defined quantities
- Notice that L cannot define I and ΦB simultaneously - this makes no sense. I, ΦB and V have most likely all been defined before as (ΦB given above in flux equation);
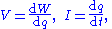
- where W = work done on charge q. Furthermore there is no definition of either I or ΦB separately – because L is defining them in the same equation.
- However, using the Lorentz force for the electromagnetic fieldElectromagnetic fieldAn electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
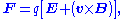
- as a single defining equation for the electric fieldElectric fieldIn physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
E and magnetic field B is allowed, since E and B are not only defined by one variable, but three; force F, velocity v and charge q. This is consistent with isolated definitions of E and B since E is defined using F and q:
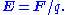
- and B defined by F, v, and q, as given above.
Limitations of definitions
Definitions vs. functions: Defining quantities can vary as a function of parameters other than those in the definition. A defining equation only defines how calculate the defined quantity, it cannot describe how the quantity varies as a function of other parameters since the function would vary from one application to another.
- Examples
- Mass density ρ is defined using mass m and volume V by but can vary as a function of temperature T and pressure p, ρ = ρ(p, T)
- The angular frequencyAngular frequencyIn physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
ω of wave propagationWave propagationWave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
is defined using the frequencyFrequencyFrequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
(or equivalently time period T) of the oscillation, as a function of wavenumberWavenumberIn the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
k, ω = ω(k). This is the dispersion relationDispersion relationIn physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
for wave propagation.
- The coefficient of restitutionCoefficient of restitutionThe coefficient of restitution of two colliding objects is a fractional value representing the ratio of speeds after and before an impact, taken along the line of the impact...
for a object colliding is defined using the speeds of separation and and approach with respect to the collision point, but depends on the nature of the surfaces in question.
Definitions vs. theorems: There is a very important difference between defining equations and general or derived results, theorems or laws. Defining equations do not find out any information about a physical system, they simply re-state one measurement in terms of others. Results, theorems, and laws, on the other hand do provide meaningful information, if only a little, since they represent a calculation for a quantity given other properties of the system, and describe how the system behaves as variables are changed.
Examples
- An example was given above for Ampere's law. Another is the conservation of momentum for N1 initial particles having initial momenta pi where i = 1, 2 ... N1, and N2 final particles having final momenta pi (some particles may explode or adhere) where j = 1, 2 ... N2, the equation of conservation reads:
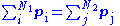
- Using the definition of momentum in terms of velocity:
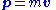
- so that for each particle:
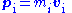and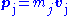 
- the conservation equation can be written as
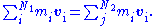
- It is identical to the previous version. No information is lost or gained by changing quantities when definitions are substituted, but the equation itself does give information about the system.
Pseudo-defining equations
Some equations, typically results from a derivation, contain quantities which may already be base quantities or have a definition, but be labelled in a different way with respect to the context of the result. These are not defining equations since they are results which apply to a physical situation – they are not quantity constructions, but can be used in the same way for calculations of the specific quantity within its scope of application.
- Examples
- Two examples in special relativitySpecial relativitySpecial relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
follow.
- Mass could be at rest or in motion (relativistic mass), relativistic mass can be pseudo-defined by
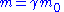
- where m0 = rest mass, m = relativistic mass and γ is the Lorentz factorLorentz factorThe Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
.
- The invariant massInvariant massThe invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
of a system could be pseudo-defined by the same equation as mass-momentum-energy invariance,
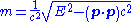
- where E = Total energy, p = Total 3-momentum of the system.
- Two examples in electromagnetism follow, neglecting relativistic effects for simplicity.
- Using SI units – not CGS or Gaussian which are fairly common in this field, the vacuum luminal speedSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
c has the exact value c = 299 792 458 ms−1 (this in itself is the definition of the metreMetreThe metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...
), and so does the vacuum permeabilityVacuum permeabilityThe physical constant μ0, commonly called the vacuum permeability, permeability of free space, or magnetic constant is an ideal, physical constant, which is the value of magnetic permeability in a classical vacuum...
μ0 (another defined value, cannot be obtained from experiment), where μ0 = 4π × 10−7 Hm−1, so the value of the vacuum permittivity can be found from the pseudo-definition
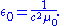
- For a charged particle (of mass m and charge q) in a uniform magnetic field B, deflected by the field in a circular helical arc at velocity v and radius of curvatureRadius of curvature (mathematics)In geometry, the radius of curvature, R, of a curve at a point is a measure of the radius of the circular arc which best approximates the curve at that point. If this value taken to be positive when the curve turns anticlockwise and negative when the curve turns clockwise...
r, where the helical trajectory inclined at an angle θ to B, the magnetic force is the centripetal forceCentripetal forceCentripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
, so the force F acting on the particle is;
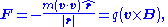
- reducing to scalar form and solving for |B||r|;
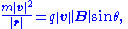
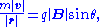
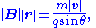
- serves as a pseudo-definition for the magnetic rigidity of the particle.
Notice that these are all derived results from their respective theories – not proper definitions.
Space
Important applied base units for space and time are below. AreaAreaArea is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
and volumeVolumeVolume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
are of course derived from length, but included for completeness as they occur frequently in many derived quantities, in particular densities.
(Common) Quantity name/s (Common) Quantity symbol SI unit Dimension (Spatial) position (vector) r, R, a, d m [L] Angular position, angle of rotation (can be treated as vector or scalar) θ, θ rad dimensionless Area, cross-section A, S, Ω m2 [L]2 Vector area (Magnitude of surface area, directed normal to tangent TangentIn geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
ial plane of surface)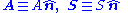
m2 [L]2 Volume τ, V m3 [L]3
Densities, flows, gradients, and moments
Important and convenient derived quantities such as densities, fluxFluxIn the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
es, flowFlow-Relating to the movement of material:* Fluid dynamics, or fluid flow, the motion of a gas or liquid* Environmental flow, the amount of water necessary in a watercourse to maintain a healthy ecosystem* Flow chemistry, a chemical reaction run in a continuous stream...
s, currentCurrent- Science and Mathematics :* Electric current* Current , including** Ocean currents** Air currents** Current - currents in rivers and streams* Current density, mathematical concept unifying electric current, fluid current, and others...
s are associated with many quantities. Sometimes different terms such as current density and flux density, rate, frequency and current, are used interchangeably in the same context, sometimes they are used uniqueley.
To clarify these effective template derived quantities, we let q be any quantity within some scope of context (not necessarily base quantities) and present in the table below some of the most commonly used symbols where applicable, their definitions, usage, SI units and SI dimensions - where [q] is the dimension of q.
For time derivatives, specific, molar, and flux densities of quantities there is no one symbol, nomenclature depends on subject, though time derivatives can be generally written using overdot notation. For generality we use qm, qn, and F respectively. No symbol is necessarily required for the gradient of a scalar field, since only the nabla/del operatorDelIn vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
∇ or gradGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
needs to be written. For spatial density, current, current density and flux, the notations are common from one context to another, differing only by a change in subscripts.
For current density,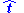
is a unit vector in the direction of flow, i.e. tangent to a flowline. Notice the dot product with the unit normal for a surface, since the amount of current passing through the surface is reduced when the current is not normal to the area. Only the current passing perpendicular to the surface contributes to the current passing through the surface, no current passes in the (tangential) plane of the surface.
The calculus notations below can be used synonymously.
If X is a n-variableMultivariable calculusMultivariable calculus is the extension of calculus in one variable to calculus in more than one variable: the differentiated and integrated functions involve multiple variables, rather than just one....
functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
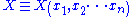, then:
- Differential The differential n-space volume elementVolume elementIn mathematics, a volume element provides a means for integrating a function with respect to volume in various coordinate systems such as spherical coordinates and cylindrical coordinates...
is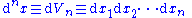
,
- Integral: The multiple integralMultiple integralThe multiple integral is a type of definite integral extended to functions of more than one real variable, for example, ƒ or ƒ...
of X over the n-space volume is
.
Quantity Typical symbols Definition Meaning, usage Dimension Quantity q q Amount of a property [q] Rate of change of quantity, Time derivative Time derivativeA time derivative is a derivative of a function with respect to time, usually interpreted as the rate of change of the value of the function. The variable denoting time is usually written as t\,.-Notation:...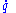
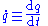
Rate of change of property with respect to time [q] [T]−1 Quantity spatial density ρ = volume density (n = 3), σ = surface density (n = 2), λ = linear density (n = 1)
No common symbol for n-space density, here ρn is used.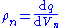
Amount of property per unit n-space
(length, area, volume or higher dimensions)[q][L]-n Specific quantity qm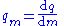 
Amount of property per unit mass [q][L]-n Molar quantity qn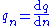 
Amount of property per mole of substance [q][L]-n Quantity gradient (if q is a scalar field Scalar fieldIn mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
.
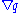
Rate of change of property with respect to position [q] [L]−1 Spectral quantity (for EM waves) qv, qν, qλ Two definitions are used, for frequency and wavelength:
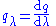
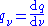
Amount of property per unit wavelength or frequency. [q][L]−1 (qλ)
[q][T] (qν)Flux, flow (synonymous) ΦF, F Two definitions are used;
Transport mechanicsTransport phenomena (engineering & physics)In engineering and physics, the study of transport phenomena concerns the exchange of mass, energy, or momentum between observed and studied engineering systems. This subject is a fundamental component of disciplines involved with fluid mechanics, heat transfer, and mass transfer...
, nuclear physicsNuclear physicsNuclear physics is the field of physics that studies the building blocks and interactions of atomic nuclei. The most commonly known applications of nuclear physics are nuclear power generation and nuclear weapons technology, but the research has provided application in many fields, including those...
/particle physicsParticle physicsParticle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
:
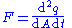
Vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
:
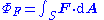
Flow of a property though a cross-section/surface boundary. [q] [T]−1 [L]−2, [F] [L]2 Flux density F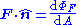 
Flow of a property though a cross-section/surface boundary per unit cross-section/surface area [F] Current i, I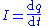 
Rate of flow of property through a cross
section/ surface boundary[q] [T]−1 Current density (sometimes called flux density in transport mechanics) j, J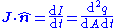 
Rate of flow of property per unit cross-section/surface area [q] [T]−1 [L]−2 Moment Moment- Science, engineering, and mathematics :* Moment , used in probability theory and statistics* Moment , several related concepts, including:** Angular momentum or moment of momentum, the rotational analog of momentum...
of quantitym, M Two definitions can be used;
q is a scalar: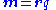
q is a vector: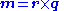
Quantity at position r has a moment about a point or axes, often relates to tendency of rotation or potential energy Potential energyIn physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
.[q] [L]
Physical quantities as coordinates over spaces of physical qualities (philosophy)
The meaning of the term physical quantity is generally well understood (everyone understands what is meant by the frequency of a periodic phenomenon, or the resistance of an electric wire). The term physical quantity does not imply a physically invariant quantity. Length for example is a physical quantity, yet it is variant under coordinate change in special and general relativity. The notion of physical quantities is so basic and intuitive in the realm of science, that it does not need to be explicitly spelled out or even mentioned. It is universally understood that scientists will (more often than not) deal with quantitative data, as opposed to qualitative data. Explicit mention and discussion of physical quantities is not part of any standard science program, and is more suited for a philosophy of science or philosophy program.
The notion of physical quantities is seldom used in physics, nor is it part of the standard physics vernacular. The idea is often misleading, as its name implies "a quantity that can be physically measured", yet is often incorrectly used to mean a physical invariant. Due to the rich complexity of physics, many different fields possess different physical invariants. There is no known physical invariant sacred in all possible fields of physics. Energy, space, momentum, torque, position, and length (just to name a few) are all found to be experimentally variant in some particular scale and system. Additionally, the notion that it is possible to measure "physical quantities" comes into question, particular in quantum field theory and normalization techniques. As infinities are produced by the theory, the actual “measurements” made are not really those of the physical universe (as we cannot measure infinities), they are those of the renormalization scheme which is expressly depended on our measurement scheme, coordinate system and metric system.
It is not always possible to define the distance between two points of any quality space, and this distance is —inside a given theoretical context— not uniquely defined. The notion of a distance, even in the context of quality space, relies on a concept of a metric space. Without a metric space, any notion of distance, physical or otherwise is undefined.
Sources
- Cook, Alan H. The observational foundations of physics, Cambridge, 1994. ISBN 0-521-45597-
- Essential Principles of Physics, P.M. Whelan, M.J. Hodgeson, 2nd Edition, 1978, John Murray, ISBN 0 7195 3382 1
- Encyclopaedia of Physics, R.G. Lerner, G.L. Trigg, 2nd Edition, VHC Publishers, Hans Warlimont, Springer, 2005, pp 12–13
- Physics for Scientists and Engineers: With Modern Physics (6th Edition), P.A. Tipler, G. Mosca, W.H. Freeman and Co, 2008, 9-781429-202657