Vector calculus
Encyclopedia
Vector calculus is a branch of mathematics
concerned with differentiation
and integration
of vector field
s, primarily in 3 dimensional Euclidean space
The term "vector calculus" is sometimes used as a synonym for the broader subject of multivariable calculus
, which includes vector calculus as well as partial differentiation
and multiple integration
. Vector calculus plays an important role in differential geometry and in the study of partial differential equation
s. It is used extensively in physics
and engineering
, especially in the description of
electromagnetic field
s, gravitational field
s and fluid flow.
Vector calculus was developed from quaternion
analysis by J. Willard Gibbs and Oliver Heaviside
near the end of the 19th century, and most of the notation and terminology was established by Gibbs and Edwin Bidwell Wilson
in their 1901 book, Vector Analysis. In the traditional form using cross products, vector calculus does not generalize to higher dimensions, while the alternative approach of geometric algebra
, which uses exterior products does generalize, as discussed below.
s (scalar-valued functions) and vector field
s (vector-valued functions). These are then combined or transformed under various operations, and integrated. In more advanced treatments, one further distinguishes pseudovector
fields and pseudoscalar
fields, which are identical to vector fields and scalar fields except that they change sign under an orientation-reversing map: for example, the curl of a vector field is a pseudovector field, and if one reflects a vector field, the curl points in the opposite direction. This distinction is clarified and elaborated in geometric algebra, as described below.
scalar multiplication
: multiplication of a scalar field and a vector field, yielding a vector field:
;
vector addition: addition of two vector fields, yielding a vector field:
;
dot product
: multiplication of two vector fields, yielding a scalar field:
;
cross product
: multiplication of two vector fields, yielding a vector field: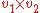
.
There are also two triple product
s: the scalar triple product and the vector triple product, but these are less used.
s defined on scalar or vector fields, which are typically expressed in terms of the del
operator (
). The four most important differential operations in vector calculus are:
where the curl and divergence differ because the former uses a cross product
and the latter a dot product
, and f denotes a scalar field and F denotes a vector field. A quantity called the Jacobian is useful for studying functions when both the domain and range of the function are multivariable, such as a change of variables
during integration.
to higher dimensions:
,
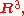which has additional structure beyond simply being a 3-dimensional real vector space, namely: an inner product (the dot product
), which gives a notion of length (and hence angle), and an orientation
, which gives a notion of left-handed and right-handed. These structures give rise to a volume form
, and also the cross product
, which is used pervasively in vector calculus.
The gradient and divergence only require the inner product, while the curl and the cross product also requires the handedness of the coordinate system
to be taken into account (see cross product and handedness for more detail).
Vector calculus can be defined on other 3-dimensional real vector spaces if they have an inner product (or more generally a symmetric nondegenerate form) and an orientation; note that this is less data than an isomorphism to Euclidean space, as it does not require a set of coordinates (a frame of reference), which reflects the fact that vector calculus is invariant under rotations (the special orthogonal group SO(3)).
More generally, vector calculus can be defined on any 3-dimensional oriented Riemannian manifold
, or more generally pseudo-Riemannian manifold
. This structure simply means that the tangent space
at each point has an inner product (more generally, a symmetric nondegenerate form) and an orientation, or more globally that there is a symmetric nondegenerate metric tensor
and an orientation, and works because vector calculus is defined in terms of tangent vectors at each point.
), while curl and cross product do not generalize as directly.
From a general point of view, the various fields in (3-dimensional) vector calculus are uniformly seen as being k-vector fields: scalar fields are 0-vector fields, vector fields are 1-vector fields, pseudovector fields are 2-vector fields, and pseudoscalar fields are 3-vector fields. In higher dimensions there are additional types of fields (scalar/vector/pseudovector/pseudoscalar corresponding to 0/1/n−1/n dimensions, which is exhaustive in dimension 3), so one cannot only work with (pseudo)scalars and (pseudo)vectors.
In any dimension, assuming a nondegenerate form, grad of a scalar function is a vector field, and div of a vector field is a scalar function, but only in dimension 3 and 7http://www.springerlink.com/content/r3p3602pq2t10036/ (and, trivially, dimension 0) is the curl of a vector field a vector field, and only in 3 or 7 dimensions can a cross product be defined (generalizations in other dimensionalities either require
vectors to yield 1 vector, or are alternative Lie algebra
s, which are more general antisymmetric bilinear products). The generalization of grad and div, and how curl may be generalized is elaborated at Curl: Generalizations; in brief, the curl of a vector field is a bivector
field, which may be interpreted as the special orthogonal Lie algebra of infinitesimal rotations; however, this cannot be identified with a vector field because the dimensions differ - there are 3 dimensions of rotations in 3 dimensions, but 6 dimensions of rotations in 4 dimensions (and more generally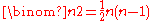
dimensions of rotations in n dimensions).
There are two important alternative generalizations of vector calculus. The first, geometric algebra
, uses k-vector
fields instead of vector fields (in 3 or fewer dimensions, every k-vector field can be identified with a scalar function or vector field, but this is not true in higher dimensions). This replaces the cross product, which is specific to 3 dimensions, taking in two vector fields and giving as output a vector field, with the exterior product, which exists in all dimensions and takes in two vector fields, giving as output a bivector (2-vector) field. This product yields Clifford algebra
s as the algebraic structure on vector spaces (with an orientation and nondegenerate form). Geometric algebra is mostly used in generalizations of physics and other applied fields to higher dimensions.
The second generalization uses differential form
s (k-covector fields) instead of vector fields or k-vector fields, and is widely used in mathematics, particularly in differential geometry, geometric topology
, and harmonic analysis
, in particular yielding Hodge theory
on oriented pseudo-Riemannian manifolds. From this point of view, grad, curl, and div correspond to the differential of 0-forms, 1-forms, and 2-forms, respectively, and the key theorems of vector calculus are all special cases of the general form of Stokes' theorem
.
From the point of view of both of these generalizations, vector calculus implicitly identifies mathematically distinct objects, which makes the presentation more elegant but the underlying mathematical structure and generalizations less clear.
From the point of view of geometric algebra, vector calculus implicitly identifies k-vector fields with vector fields or scalar functions: 0-vectors and 3-vectors with scalars, 1-vectors and 2-vectors with vectors. From the point of view of differential forms, vector calculus implicitly identifies k-forms with scalar fields or vector fields: 0-forms and 3-forms with scalar fields, 1-forms and 2-forms with vector fields. Thus for example the curl naturally takes as input a vector field, but naturally has as output a 2-vector field or 2-form (hence pseudovector field), which is then interpreted as a vector field, rather than directly taking a vector field to a vector field; this is reflected in the curl of a vector field in higher dimensions not having as output a vector field.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
concerned with differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
and integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s, primarily in 3 dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
The term "vector calculus" is sometimes used as a synonym for the broader subject of multivariable calculusMultivariable calculus
Multivariable calculus is the extension of calculus in one variable to calculus in more than one variable: the differentiated and integrated functions involve multiple variables, rather than just one....
, which includes vector calculus as well as partial differentiation
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
and multiple integration
Multiple integral
The multiple integral is a type of definite integral extended to functions of more than one real variable, for example, ƒ or ƒ...
. Vector calculus plays an important role in differential geometry and in the study of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s. It is used extensively in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, especially in the description of
electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
s, gravitational field
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
s and fluid flow.
Vector calculus was developed from quaternion
Quaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
analysis by J. Willard Gibbs and Oliver Heaviside
Oliver Heaviside
Oliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...
near the end of the 19th century, and most of the notation and terminology was established by Gibbs and Edwin Bidwell Wilson
Edwin Bidwell Wilson
Edwin Bidwell Wilson was an American mathematician and polymath. He was the sole protégé of Yale's physicist Josiah Willard Gibbs and was mentor to MIT economist Paul Samuelson. He received his AB from Harvard College in 1899 and his PhD from Yale University in 1901, working under Gibbs.E.B...
in their 1901 book, Vector Analysis. In the traditional form using cross products, vector calculus does not generalize to higher dimensions, while the alternative approach of geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
, which uses exterior products does generalize, as discussed below.
Basic objects
The basic objects in vector calculus are scalar fieldScalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
s (scalar-valued functions) and vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s (vector-valued functions). These are then combined or transformed under various operations, and integrated. In more advanced treatments, one further distinguishes pseudovector
Pseudovector
In physics and mathematics, a pseudovector is a quantity that transforms like a vector under a proper rotation, but gains an additional sign flip under an improper rotation such as a reflection. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image...
fields and pseudoscalar
Pseudoscalar
In physics, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion such as improper rotations while a true scalar does not.The prototypical example of a pseudoscalar is the scalar triple product...
fields, which are identical to vector fields and scalar fields except that they change sign under an orientation-reversing map: for example, the curl of a vector field is a pseudovector field, and if one reflects a vector field, the curl points in the opposite direction. This distinction is clarified and elaborated in geometric algebra, as described below.
Algebraic operations
The basic algebraic (non-differential) operations in vector calculus are referred to as vector algebra, being defined for a vector space and then globally applied to a vector field, and consist of:scalar multiplication
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
: multiplication of a scalar field and a vector field, yielding a vector field:
;vector addition: addition of two vector fields, yielding a vector field:
;dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
: multiplication of two vector fields, yielding a scalar field:
;cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
: multiplication of two vector fields, yielding a vector field:
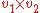.There are also two triple product
Triple product
In mathematics, the triple product is a product of three vectors. The name "triple product" is used for two different products, the scalar-valued scalar triple product and, less often, the vector-valued vector triple product....
s: the scalar triple product and the vector triple product, but these are less used.
Differential operations
Vector calculus studies various differential operatorDifferential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
s defined on scalar or vector fields, which are typically expressed in terms of the del
Del
In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
operator (
). The four most important differential operations in vector calculus are:
| Operation | Notation | Description | Domain/Range |
|---|---|---|---|
| Gradient Gradient In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change.... |
 |
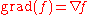Measures the rate and direction of change in a scalar field. | Maps scalar fields to vector fields. |
| Curl |  |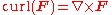
Measures the tendency to rotate about a point in a vector field. | Maps vector fields to (pseudo)vector fields. |
| Divergence Divergence In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around... |
 |
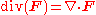Measures the magnitude of a source or sink at a given point in a vector field. | Maps vector fields to scalar fields. |
| Laplacian Laplace operator In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ... |
 |
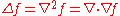A composition of the divergence and gradient operations. | Maps scalar fields to scalar fields. |
where the curl and divergence differ because the former uses a cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
and the latter a dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
, and f denotes a scalar field and F denotes a vector field. A quantity called the Jacobian is useful for studying functions when both the domain and range of the function are multivariable, such as a change of variables
Change of variables
In mathematics, a change of variables is a basic technique used to simplify problems in which the original variables are replaced with new ones; the new and old variables being related in some specified way...
during integration.
Theorems
Likewise, there are several important theorems related to these operators which generalize the fundamental theorem of calculusFundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
to higher dimensions:
| Theorem | Statement | Description |
|---|---|---|
| Gradient theorem Gradient theorem The gradient theorem, also known as the fundamental theorem of calculus for line integrals, says that a line integral through a gradient field can be evaluated by evaluating the original scalar field at the endpoints of the curve: \phi\left-\phi\left = \int_L... |
The line integral Line integral In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field... through a gradient (vector) field equals the difference in its scalar field at the endpoints of the curve Curve In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight... L. |
|
| Green's theorem Green's theorem In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C... |
 |
The integral of the scalar curl of a vector field over some region in the plane equals the line integral of the vector field over the closed curve bounding the region. |
| Stokes' theorem Stokes' theorem In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850... |
 |
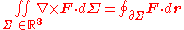The integral of the curl of a vector field over a surface Surface In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball... in  equals the line integral of the vector field over the closed curve bounding the surface. |
| Divergence theorem Divergence theorem In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem... |
 |
The integral of the divergence of a vector field over some solid equals the integral of the flux Flux In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time... through the closed surface bounding the solid. |
Different 3-manifolds
Vector calculus is initially defined for Euclidean 3-spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
,
which has additional structure beyond simply being a 3-dimensional real vector space, namely: an inner product (the dot productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
), which gives a notion of length (and hence angle), and an orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
, which gives a notion of left-handed and right-handed. These structures give rise to a volume form
Volume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
, and also the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
, which is used pervasively in vector calculus.
The gradient and divergence only require the inner product, while the curl and the cross product also requires the handedness of the coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
to be taken into account (see cross product and handedness for more detail).
Vector calculus can be defined on other 3-dimensional real vector spaces if they have an inner product (or more generally a symmetric nondegenerate form) and an orientation; note that this is less data than an isomorphism to Euclidean space, as it does not require a set of coordinates (a frame of reference), which reflects the fact that vector calculus is invariant under rotations (the special orthogonal group SO(3)).
More generally, vector calculus can be defined on any 3-dimensional oriented Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
, or more generally pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
. This structure simply means that the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at each point has an inner product (more generally, a symmetric nondegenerate form) and an orientation, or more globally that there is a symmetric nondegenerate metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
and an orientation, and works because vector calculus is defined in terms of tangent vectors at each point.
Other dimensions
Most of the analytic results are easily understood, in a more general form, using the machinery of differential geometry, of which vector calculus forms a subset. Grad and div generalize immediately to other dimensions, as do the gradient theorem, divergence theorem, and Laplacian (yielding harmonic analysisHarmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
), while curl and cross product do not generalize as directly.
From a general point of view, the various fields in (3-dimensional) vector calculus are uniformly seen as being k-vector fields: scalar fields are 0-vector fields, vector fields are 1-vector fields, pseudovector fields are 2-vector fields, and pseudoscalar fields are 3-vector fields. In higher dimensions there are additional types of fields (scalar/vector/pseudovector/pseudoscalar corresponding to 0/1/n−1/n dimensions, which is exhaustive in dimension 3), so one cannot only work with (pseudo)scalars and (pseudo)vectors.
In any dimension, assuming a nondegenerate form, grad of a scalar function is a vector field, and div of a vector field is a scalar function, but only in dimension 3 and 7http://www.springerlink.com/content/r3p3602pq2t10036/ (and, trivially, dimension 0) is the curl of a vector field a vector field, and only in 3 or 7 dimensions can a cross product be defined (generalizations in other dimensionalities either require
vectors to yield 1 vector, or are alternative Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s, which are more general antisymmetric bilinear products). The generalization of grad and div, and how curl may be generalized is elaborated at Curl: Generalizations; in brief, the curl of a vector field is a bivector
Bivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
field, which may be interpreted as the special orthogonal Lie algebra of infinitesimal rotations; however, this cannot be identified with a vector field because the dimensions differ - there are 3 dimensions of rotations in 3 dimensions, but 6 dimensions of rotations in 4 dimensions (and more generally
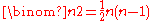dimensions of rotations in n dimensions).There are two important alternative generalizations of vector calculus. The first, geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
, uses k-vector
Multivector
In multilinear algebra, a multivector or clif is an element of the exterior algebra on a vector space, \Lambda^* V. This algebra consists of linear combinations of simple k-vectors v_1\wedge\cdots\wedge v_k."Multivector" may mean either homogeneous elements In multilinear algebra, a multivector...
fields instead of vector fields (in 3 or fewer dimensions, every k-vector field can be identified with a scalar function or vector field, but this is not true in higher dimensions). This replaces the cross product, which is specific to 3 dimensions, taking in two vector fields and giving as output a vector field, with the exterior product, which exists in all dimensions and takes in two vector fields, giving as output a bivector (2-vector) field. This product yields Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
s as the algebraic structure on vector spaces (with an orientation and nondegenerate form). Geometric algebra is mostly used in generalizations of physics and other applied fields to higher dimensions.
The second generalization uses differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s (k-covector fields) instead of vector fields or k-vector fields, and is widely used in mathematics, particularly in differential geometry, geometric topology
Geometric topology
In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...
, and harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
, in particular yielding Hodge theory
Hodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
on oriented pseudo-Riemannian manifolds. From this point of view, grad, curl, and div correspond to the differential of 0-forms, 1-forms, and 2-forms, respectively, and the key theorems of vector calculus are all special cases of the general form of Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
.
From the point of view of both of these generalizations, vector calculus implicitly identifies mathematically distinct objects, which makes the presentation more elegant but the underlying mathematical structure and generalizations less clear.
From the point of view of geometric algebra, vector calculus implicitly identifies k-vector fields with vector fields or scalar functions: 0-vectors and 3-vectors with scalars, 1-vectors and 2-vectors with vectors. From the point of view of differential forms, vector calculus implicitly identifies k-forms with scalar fields or vector fields: 0-forms and 3-forms with scalar fields, 1-forms and 2-forms with vector fields. Thus for example the curl naturally takes as input a vector field, but naturally has as output a 2-vector field or 2-form (hence pseudovector field), which is then interpreted as a vector field, rather than directly taking a vector field to a vector field; this is reflected in the curl of a vector field in higher dimensions not having as output a vector field.
See also
- Vector calculus identities
- Del in cylindrical and spherical coordinatesDel in cylindrical and spherical coordinatesThis is a list of some vector calculus formulae of general use in working with various curvilinear coordinate systems.- Note :* This page uses standard physics notation. For spherical coordinates, \theta is the angle between the z axis and the radius vector connecting the origin to the point in...
- Directional derivativeDirectional derivativeIn mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
- Irrotational vector fieldIrrotational vector fieldIn vector calculus a conservative vector field is a vector field which is the gradient of a function, known in this context as a scalar potential. Conservative vector fields have the property that the line integral from one point to another is independent of the choice of path connecting the two...
- Solenoidal vector field
- Laplacian vector field
- Helmholtz decompositionHelmholtz decompositionIn physics and mathematics, in the area of vector calculus, Helmholtz's theorem, also known as the fundamental theorem of vector calculus, states that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational vector field and a...
- Orthogonal coordinatesOrthogonal coordinatesIn mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
- Skew coordinatesSkew coordinatesA system of skew coordinates is a coordinate system where the coordinate surfaces are not orthogonal, in contrast to orthogonal coordinates.Skew coordinates tend to be more complicated to work with compared to orthogonal coordinates since the metric tensor will have nonzero off-diagonal components,...
- Curvilinear coordinatesCurvilinear coordinatesCurvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given...
- TensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
External links
- Vector Calculus Video Lectures from University of New South WalesUniversity of New South WalesThe University of New South Wales , is a research-focused university based in Kensington, a suburb in Sydney, New South Wales, Australia...
on Academic EarthAcademic EarthAcademic Earth is a website launched March 24, 2009, by Richard Ludlow and co-founders Chris Bruner and Liam Pisano,which offers free online video lectures from universities such as UC Berkeley, UCLA, University of Michigan, Harvard, MIT, Princeton, Stanford, and Yale in the subjects of Astronomy,... - A survey of the improper use of ∇ in vector analysis (1994) Tai, Chen
- Expanding vector analysis to an oblique coordinate system
- Vector Analysis: A Text-book for the Use of Students of Mathematics and Physics, (based upon the lectures of Willard Gibbs) by Edwin Bidwell WilsonEdwin Bidwell WilsonEdwin Bidwell Wilson was an American mathematician and polymath. He was the sole protégé of Yale's physicist Josiah Willard Gibbs and was mentor to MIT economist Paul Samuelson. He received his AB from Harvard College in 1899 and his PhD from Yale University in 1901, working under Gibbs.E.B...
, published 1902. - Earliest Known Uses of Some of the Words of Mathematics: Vector Analysis