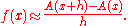
Fundamental theorem of calculus
Encyclopedia
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration
can be reversed by a differentiation. The first part is also important because it guarantees the existence of antiderivative
s for continuous function
s.
The second part, sometimes called the second fundamental theorem of calculus, allows one to compute the definite integral of a function by using any one of its infinitely many antiderivative
s. This part of the theorem has invaluable practical applications, because it markedly simplifies the computation of definite integrals.
The first published statement and proof of a restricted version of the fundamental theorem was by James Gregory
(1638–1675). Isaac Barrow
(1630–1677) proved a more generalized version of the theorem, while Barrow's student Isaac Newton
(1643–1727) completed the development of the surrounding mathematical theory. Gottfried Leibniz
(1646–1716) systematized the knowledge into a calculus for infinitesimal quantities.
changes in a quantity over time (or over some other quantity) adds up to the net change in the quantity.
In the case of a particle traveling in a straight line, its position, x, is given by x(t) where t is time and x(t) means that x is a function
of t. The derivative of this function is equal to the infinitesimal change in quantity, dx, per infinitesimal change in time, dt (of course, the derivative itself is dependent on time). This change in displacement per change in time is the velocity v of the particle. In Leibniz's notation
:
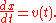
Rearranging this equation, it follows that:
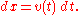
By the logic above, a change in x (or Δx) is the sum of the infinitesimal changes dx. It is also equal to the sum of the infinitesimal products of the derivative and time. This infinite summation is integration; hence, the integration operation allows the recovery of the original function from its derivative. It can be concluded that this operation works in reverse; the result of the integral can be differentiated to recover the original function.
The area under the curve between x and x + h could be computed by finding the area between 0 and x + h, then subtracting the area between 0 and x. In other words, the area of this “sliver” would be .
There is another way to estimate the area of this same sliver. h is multiplied by ƒ(x) to find the area of a rectangle that is approximately the same size as this sliver. It is intuitive that the approximation improves as h becomes smaller.
At this point, it is true A(x + h) − A(x) is approximately equal to ƒ(x)·h. In other words, , with this approximation becoming an equality as h approaches 0 in the limit
.
When both sides of the equation are divided by h:
As h approaches 0, it can be seen that the right hand side of this equation is simply the derivative
A’(x) of the area function A(x). The left-hand side of the equation simply remains ƒ(x), since no h is present.
It can thus be shown, in an informal way, that . That is, the derivative of the area function A(x) is the original function ƒ(x); or, the area function is simply the antiderivative
of the original function.
Computing the derivative of a function and “finding the area” under its curve are "opposite" operations. This is the crux of the Fundamental Theorem of Calculus. Most of the theorem's proof is devoted to showing that the area function A(x) exists in the first place, under the right conditions.
, while the second part deals with the relationship between antiderivatives and definite integrals.
Let ƒ be a continuous real-valued function defined on a closed interval [a, b]. Let F be the function defined, for all x in [a, b], by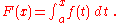
Then, F is continuous on [a, b], differentiable on the open interval (a, b), and
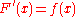
for all x in (a, b).
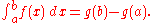
The corollary assumes continuity on the whole interval. This result is strengthened slightly in the following theorem.
Let ƒ be a real-valued function defined on a closed interval [a, b] that admits an antiderivative
g on [a, b]. That is, ƒ and g are functions such that for all x in [a, b],
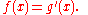
If ƒ is integrable on [a, b] then
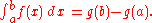
Notice that the Second part is somewhat stronger than the Corollary because it does not assume that ƒ is continuous.
Note that when an antiderivative g exists, then there are infinitely many antiderivatives for ƒ, obtained by adding to g an arbitrary constant. Also, by the first part of the theorem, antiderivatives of ƒ always exist when ƒ is continuous.
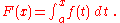
For any two numbers x1 and x1 + Δx in [a, b], we have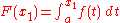
and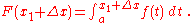
Subtracting the two equations gives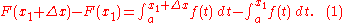
It can be shown that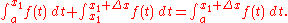
Manipulating this equation gives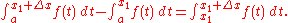
Substituting the above into (1) results in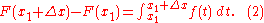
According to the mean value theorem
for integration, there exists a c in [x1, x1 + Δx] such that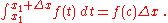
Substituting the above into (2) we get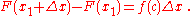
Dividing both sides by Δx gives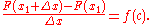
Take the limit as Δx → 0 on both sides of the equation.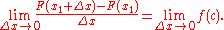
The expression on the left side of the equation is the definition of the derivative of F at x1.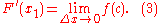
To find the other limit, we will use the squeeze theorem
. The number c is in the interval [x1, x1 + Δx], so x1 ≤ c ≤ x1 + Δx.
Also,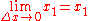
and 
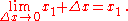
Therefore, according to the squeeze theorem,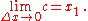
Substituting into (3), we get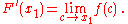
The function f is continuous at c, so the limit can be taken inside the function. Therefore, we get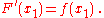
which completes the proof.
(Leithold et al, 1996)
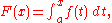with ƒ continuous on [a, b]. If g is an antiderivative of ƒ, then g and F have the same derivative, by the first part of the theorem. It follows by the mean value theorem that there is a number c such that , for all x in [a, b]. Letting ,
which means c = − g(a). In other words F(x) = , and so
.
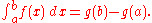
Let ƒ be (Riemann) integrable on the interval [a, b], and let ƒ admit an antiderivative F on [a, b]. Begin with the quantity . Let there be numbers x1, ..., xn
such that
It follows that
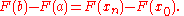
Now, we add each F(xi) along with its additive inverse, so that the resulting quantity is equal:
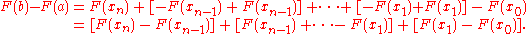
The above quantity can be written as the following sum:
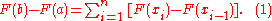
Next we will employ the mean value theorem
. Stated briefly,
Let F be continuous on the closed interval [a, b] and differentiable on the open interval (a, b). Then there exists some c in (a, b) such that
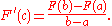
It follows that
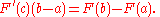
The function F is differentiable on the interval [a, b]; therefore, it is also differentiable and continuous on each interval . According to the mean value theorem (above),
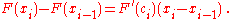
Substituting the above into (1), we get
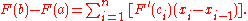
The assumption implies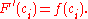
Also,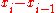 
can be expressed as 
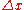of partition 
.
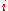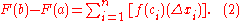
Notice that we are describing the area of a rectangle, with the width times the height, and we are adding the areas together. Each rectangle, by virtue of the Mean Value Theorem
, describes an approximation of the curve section it is drawn over. Also notice that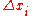
need not be the same for all values of i, or in other words that the width of the rectangles can differ. What we have to do is approximate the curve with n rectangles. Now, as the size of the partitions get smaller and n increases, resulting in more partitions to cover the space, we will get closer and closer to the actual area of the curve.
By taking the limit of the expression as the norm of the partitions approaches zero, we arrive at the Riemann integral
. We know that this limit exists because ƒ was assumed to be integrable. That is, we take the limit as the largest of the partitions approaches zero in size, so that all other partitions are smaller and the number of partitions approaches infinity.
So, we take the limit on both sides of (2). This gives us
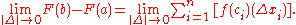
Neither F(b) nor F(a) is dependent on ||Δ||, so the limit on the left side remains F(b) − F(a).
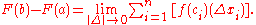
The expression on the right side of the equation defines the integral over ƒ from a to b. Therefore, we obtain
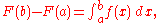
which completes the proof.
It almost looks like the first part of the theorem follows directly from the second, because the equation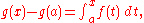
where g is an antiderivative of ƒ, implies that 
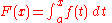has the same derivative as g, and therefore . This argument only works if we already know that ƒ has an antiderivative, and the only way we know that all continuous functions have antiderivatives is by the first part of the Fundamental Theorem.
For example if ƒ(x) = e−x2, then ƒ has an antiderivative, namely
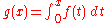
and there is no simpler expression for this function. It is therefore important not to interpret the second part of the theorem as the definition of the integral. Indeed, there are many functions that are integrable but lack antiderivatives that can be written as an elementary function. Conversely, many functions that have antiderivatives are not Riemann integrable (see Volterra's function
).
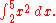
Here,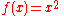
and we can use 
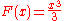as the antiderivative. Therefore:
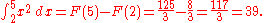
Or, more generally, that
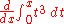
is to be calculated. Here,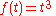
and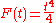 
can be used as the antiderivative. Therefore:
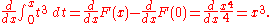
Or, equivalently,
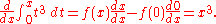
function on and x0 is a number in such that ƒ is continuous at x0, then
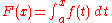
is differentiable for x = x0 with F' (x0) = ƒ(x0). We can relax the conditions on ƒ still further and suppose that it is merely locally integrable. In that case, we can conclude that the function F is differentiable almost everywhere
and F' (x) = ƒ(x) almost everywhere. On the real line this statement is equivalent to Lebesgue's differentiation theorem
. These results remain true for the Henstock–Kurzweil integral which allows a larger class of integrable functions .
The most familiar extensions of the Fundamental theorem of calculus in two dimensions are Green's theorem
.
In higher dimensions Lebesgue's differentiation theorem generalizes the Fundamental theorem of calculus by stating that for almost every x, the average value of a function ƒ over a ball of radius r centered at x will tend to ƒ(x) as r tends to 0.
Part II of the theorem is true for any Lebesgue integrable function ƒ which has an antiderivative F (not all integrable functions do, though). In other words, if a real function F on [a, b] admits a derivative ƒ(x) at every point x of and if this derivative ƒ is Lebesgue integrable on [a, b], then
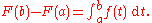
This result may fail for continuous functions F that admit a derivative ƒ(x) at almost every point x, as the example of the Cantor function
shows. But the result remains true if F is absolutely continuous
: in that case, F admits a derivative ƒ(x) at almost every point x and, as in the formula above, is equal to the integral of ƒ on [a, b].
The conditions of this theorem may again be relaxed by considering the integrals involved as Henstock–Kurzweil integrals. Specifically, if a continuous function F(x) admits a derivative ƒ(x) at all but countably many points, then ƒ(x) is Henstock–Kurzweil integrable and is equal to the integral of ƒ on [a, b]. The difference here is that the integrability of ƒ does not need to be assumed.
The version of Taylor's theorem
which expresses the error term as an integral can be seen as a generalization of the Fundamental Theorem.
There is a version of the theorem for complex
functions: suppose U is an open set in C and ƒ : U → C is a function which has a holomorphic
antiderivative F on U. Then for every curve γ : [a, b] → U, the curve integral can be computed as
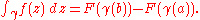
The fundamental theorem can be generalized to curve and surface integrals in higher dimensions and on manifold
s. One such generalization offered by the calculus of moving surfaces is the time evolution of integrals
.
One of the most powerful statements in this direction is Stokes' theorem
: Let M be an oriented piecewise
smooth manifold
of dimension
n and let
be an n−1 form that is a compactly supported differential form
on M of class C1. If ∂M denotes the boundary
of M with its induced orientation
, then
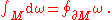
Here
is the exterior derivative
, which is defined using the manifold structure only.
The theorem is often used in situations where M is an embedded oriented submanifold of some bigger manifold on which the form
is defined.
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
can be reversed by a differentiation. The first part is also important because it guarantees the existence of antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
s for continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s.
The second part, sometimes called the second fundamental theorem of calculus, allows one to compute the definite integral of a function by using any one of its infinitely many antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
s. This part of the theorem has invaluable practical applications, because it markedly simplifies the computation of definite integrals.
The first published statement and proof of a restricted version of the fundamental theorem was by James Gregory
James Gregory (astronomer and mathematician)
James Gregory FRS was a Scottish mathematician and astronomer. He described an early practical design for the reflecting telescope – the Gregorian telescope – and made advances in trigonometry, discovering infinite series representations for several trigonometric functions.- Biography :The...
(1638–1675). Isaac Barrow
Isaac Barrow
Isaac Barrow was an English Christian theologian, and mathematician who is generally given credit for his early role in the development of infinitesimal calculus; in particular, for the discovery of the fundamental theorem of calculus. His work centered on the properties of the tangent; Barrow was...
(1630–1677) proved a more generalized version of the theorem, while Barrow's student Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
(1643–1727) completed the development of the surrounding mathematical theory. Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
(1646–1716) systematized the knowledge into a calculus for infinitesimal quantities.
Physical intuition
Intuitively, the theorem simply states that the sum of infinitesimalInfinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
changes in a quantity over time (or over some other quantity) adds up to the net change in the quantity.
In the case of a particle traveling in a straight line, its position, x, is given by x(t) where t is time and x(t) means that x is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of t. The derivative of this function is equal to the infinitesimal change in quantity, dx, per infinitesimal change in time, dt (of course, the derivative itself is dependent on time). This change in displacement per change in time is the velocity v of the particle. In Leibniz's notation
Leibniz notation
In calculus, Leibniz's notation, named in honor of the 17th-century German philosopher and mathematician Gottfried Wilhelm Leibniz, uses the symbols dx and dy to represent "infinitely small" increments of x and y, just as Δx and Δy represent finite increments of x and y...
:
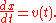
Rearranging this equation, it follows that:
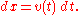
By the logic above, a change in x (or Δx) is the sum of the infinitesimal changes dx. It is also equal to the sum of the infinitesimal products of the derivative and time. This infinite summation is integration; hence, the integration operation allows the recovery of the original function from its derivative. It can be concluded that this operation works in reverse; the result of the integral can be differentiated to recover the original function.
Geometric intuition
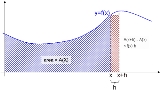
For a continuous function whose graph is plotted as a curve, each value of x has a corresponding area function A(x), representing the area beneath the curve between 0 and x. The function A(x) may not be known, but it is given that it represents the area under the curve.The area under the curve between x and x + h could be computed by finding the area between 0 and x + h, then subtracting the area between 0 and x. In other words, the area of this “sliver” would be .
There is another way to estimate the area of this same sliver. h is multiplied by ƒ(x) to find the area of a rectangle that is approximately the same size as this sliver. It is intuitive that the approximation improves as h becomes smaller.
At this point, it is true A(x + h) − A(x) is approximately equal to ƒ(x)·h. In other words, , with this approximation becoming an equality as h approaches 0 in the limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
.
When both sides of the equation are divided by h:
As h approaches 0, it can be seen that the right hand side of this equation is simply the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
A’(x) of the area function A(x). The left-hand side of the equation simply remains ƒ(x), since no h is present.
It can thus be shown, in an informal way, that . That is, the derivative of the area function A(x) is the original function ƒ(x); or, the area function is simply the antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
of the original function.
Computing the derivative of a function and “finding the area” under its curve are "opposite" operations. This is the crux of the Fundamental Theorem of Calculus. Most of the theorem's proof is devoted to showing that the area function A(x) exists in the first place, under the right conditions.
Formal statements
There are two parts to the Fundamental Theorem of Calculus. Loosely put, the first part deals with the derivative of an antiderivativeAntiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
, while the second part deals with the relationship between antiderivatives and definite integrals.
First part
This part is sometimes referred to as the First Fundamental Theorem of Calculus.Let ƒ be a continuous real-valued function defined on a closed interval [a, b]. Let F be the function defined, for all x in [a, b], by
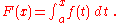
Then, F is continuous on [a, b], differentiable on the open interval (a, b), and
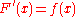
for all x in (a, b).
Corollary
The fundamental theorem is often employed to compute the definite integral of a function ƒ for which an antiderivative g is known. Specifically, if ƒ is a real-valued continuous function on [a, b], and g is an antiderivative of ƒ in [a, b], then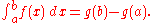The corollary assumes continuity on the whole interval. This result is strengthened slightly in the following theorem.
Second part
This part is sometimes referred to as the Second Fundamental Theorem of Calculus or the Newton–Leibniz Axiom.Let ƒ be a real-valued function defined on a closed interval [a, b] that admits an antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
g on [a, b]. That is, ƒ and g are functions such that for all x in [a, b],
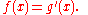
If ƒ is integrable on [a, b] then
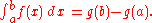
Notice that the Second part is somewhat stronger than the Corollary because it does not assume that ƒ is continuous.
Note that when an antiderivative g exists, then there are infinitely many antiderivatives for ƒ, obtained by adding to g an arbitrary constant. Also, by the first part of the theorem, antiderivatives of ƒ always exist when ƒ is continuous.
Proof of the first part
For a given f(t), define the function F(x) as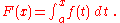For any two numbers x1 and x1 + Δx in [a, b], we have
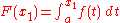
and
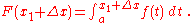
Subtracting the two equations gives
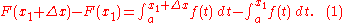
It can be shown that
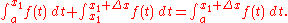
Manipulating this equation gives
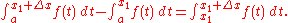
Substituting the above into (1) results in
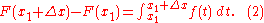
According to the mean value theorem
Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
for integration, there exists a c in [x1, x1 + Δx] such that
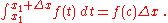
Substituting the above into (2) we get
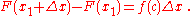
Dividing both sides by Δx gives
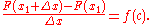
- Notice that the expression on the left side of the equation is Newton's difference quotientDifference quotientThe primary vehicle of calculus and other higher mathematics is the function. Its "input value" is its argument, usually a point expressible on a graph...
for F at x1.
Take the limit as Δx → 0 on both sides of the equation.
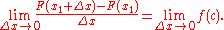
The expression on the left side of the equation is the definition of the derivative of F at x1.
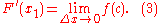
To find the other limit, we will use the squeeze theorem
Squeeze theorem
In calculus, the squeeze theorem is a theorem regarding the limit of a function....
. The number c is in the interval [x1, x1 + Δx], so x1 ≤ c ≤ x1 + Δx.
Also,
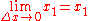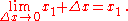
and Therefore, according to the squeeze theorem,
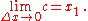
Substituting into (3), we get
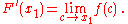
The function f is continuous at c, so the limit can be taken inside the function. Therefore, we get
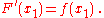
which completes the proof.
(Leithold et al, 1996)
Proof of the corollary
Let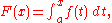 with ƒ continuous on [a, b]. If g is an antiderivative of ƒ, then g and F have the same derivative, by the first part of the theorem. It follows by the mean value theorem that there is a number c such that , for all x in [a, b]. Letting ,which means c = − g(a). In other words F(x) = , and so
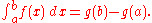
Proof of the second part
This is a limit proof by Riemann sumsRiemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
.
Let ƒ be (Riemann) integrable on the interval [a, b], and let ƒ admit an antiderivative F on [a, b]. Begin with the quantity . Let there be numbers x1, ..., xn
such that
It follows that
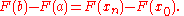
Now, we add each F(xi) along with its additive inverse, so that the resulting quantity is equal:
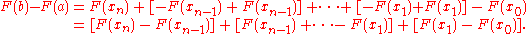
The above quantity can be written as the following sum:
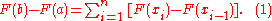
Next we will employ the mean value theorem
Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
. Stated briefly,
Let F be continuous on the closed interval [a, b] and differentiable on the open interval (a, b). Then there exists some c in (a, b) such that
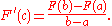
It follows that
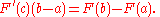
The function F is differentiable on the interval [a, b]; therefore, it is also differentiable and continuous on each interval . According to the mean value theorem (above),
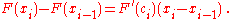
Substituting the above into (1), we get
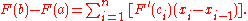
The assumption implies
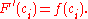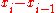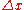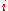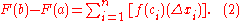
Also, can be expressed as of partition .Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
, describes an approximation of the curve section it is drawn over. Also notice that
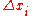need not be the same for all values of i, or in other words that the width of the rectangles can differ. What we have to do is approximate the curve with n rectangles. Now, as the size of the partitions get smaller and n increases, resulting in more partitions to cover the space, we will get closer and closer to the actual area of the curve.By taking the limit of the expression as the norm of the partitions approaches zero, we arrive at the Riemann integral
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
. We know that this limit exists because ƒ was assumed to be integrable. That is, we take the limit as the largest of the partitions approaches zero in size, so that all other partitions are smaller and the number of partitions approaches infinity.
So, we take the limit on both sides of (2). This gives us
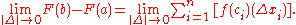
Neither F(b) nor F(a) is dependent on ||Δ||, so the limit on the left side remains F(b) − F(a).
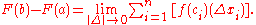
The expression on the right side of the equation defines the integral over ƒ from a to b. Therefore, we obtain
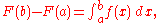
which completes the proof.
It almost looks like the first part of the theorem follows directly from the second, because the equation
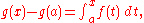where g is an antiderivative of ƒ, implies that 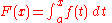has the same derivative as g, and therefore . This argument only works if we already know that ƒ has an antiderivative, and the only way we know that all continuous functions have antiderivatives is by the first part of the Fundamental Theorem.For example if ƒ(x) = e−x2, then ƒ has an antiderivative, namely
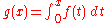
and there is no simpler expression for this function. It is therefore important not to interpret the second part of the theorem as the definition of the integral. Indeed, there are many functions that are integrable but lack antiderivatives that can be written as an elementary function. Conversely, many functions that have antiderivatives are not Riemann integrable (see Volterra's function
Volterra's function
In mathematics, Volterra's function, named for Vito Volterra, is a real-valued function V defined on the real line R with the following curious combination of properties:* V is differentiable everywhere...
).
Examples
As an example, suppose the following is to be calculated: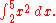Here,
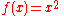and we can use 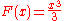as the antiderivative. Therefore: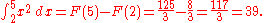Or, more generally, that
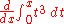
is to be calculated. Here,
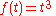and 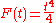can be used as the antiderivative. Therefore: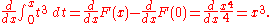Or, equivalently,
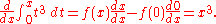
Generalizations
We don't need to assume continuity of ƒ on the whole interval. Part I of the theorem then says: if ƒ is any Lebesgue integrableLebesgue integration
In mathematics, Lebesgue integration, named after French mathematician Henri Lebesgue , refers to both the general theory of integration of a function with respect to a general measure, and to the specific case of integration of a function defined on a subset of the real line or a higher...
function on and x0 is a number in such that ƒ is continuous at x0, then
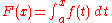
is differentiable for x = x0 with F
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
and F
Lebesgue differentiation theorem
In mathematics, the Lebesgue differentiation theorem is a theorem of real analysis, which states that for almost every point, the value of an integrable function is the limit of infinitesimal averages taken about the point...
. These results remain true for the Henstock–Kurzweil integral which allows a larger class of integrable functions .
The most familiar extensions of the Fundamental theorem of calculus in two dimensions are Green's theorem
Green's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
.
In higher dimensions Lebesgue's differentiation theorem generalizes the Fundamental theorem of calculus by stating that for almost every x, the average value of a function ƒ over a ball of radius r centered at x will tend to ƒ(x) as r tends to 0.
Part II of the theorem is true for any Lebesgue integrable function ƒ which has an antiderivative F (not all integrable functions do, though). In other words, if a real function F on [a, b] admits a derivative ƒ(x) at every point x of and if this derivative ƒ is Lebesgue integrable on [a, b], then
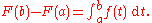
This result may fail for continuous functions F that admit a derivative ƒ(x) at almost every point x, as the example of the Cantor function
Cantor function
In mathematics, the Cantor function, named after Georg Cantor, is an example of a function that is continuous, but not absolutely continuous. It is also referred to as the Devil's staircase.-Definition:See figure...
shows. But the result remains true if F is absolutely continuous
Absolute continuity
In mathematics, the relationship between the two central operations of calculus, differentiation and integration, stated by fundamental theorem of calculus in the framework of Riemann integration, is generalized in several directions, using Lebesgue integration and absolute continuity...
: in that case, F admits a derivative ƒ(x) at almost every point x and, as in the formula above, is equal to the integral of ƒ on [a, b].
The conditions of this theorem may again be relaxed by considering the integrals involved as Henstock–Kurzweil integrals. Specifically, if a continuous function F(x) admits a derivative ƒ(x) at all but countably many points, then ƒ(x) is Henstock–Kurzweil integrable and is equal to the integral of ƒ on [a, b]. The difference here is that the integrability of ƒ does not need to be assumed.
The version of Taylor's theorem
Taylor's theorem
In calculus, Taylor's theorem gives an approximation of a k times differentiable function around a given point by a k-th order Taylor-polynomial. For analytic functions the Taylor polynomials at a given point are finite order truncations of its Taylor's series, which completely determines the...
which expresses the error term as an integral can be seen as a generalization of the Fundamental Theorem.
There is a version of the theorem for complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
functions: suppose U is an open set in C and ƒ : U → C is a function which has a holomorphic
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
antiderivative F on U. Then for every curve γ : [a, b] → U, the curve integral can be computed as
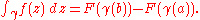
The fundamental theorem can be generalized to curve and surface integrals in higher dimensions and on manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s. One such generalization offered by the calculus of moving surfaces is the time evolution of integrals
Time evolution of integrals
In many applications, one needs to calculate the rate of change of a volume or surface integral whose domain of integration, as well as the integrand, are functions of a particular parameter...
.
One of the most powerful statements in this direction is Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
: Let M be an oriented piecewise
Piecewise
On mathematics, a piecewise-defined function is a function whose definition changes depending on the value of the independent variable...
smooth manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
of dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
n and let
be an n−1 form that is a compactly supported differential formDifferential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
on M of class C1. If ∂M denotes the boundary
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
of M with its induced orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
, then
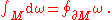
Here
is the exterior derivativeExterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
, which is defined using the manifold structure only.
The theorem is often used in situations where M is an embedded oriented submanifold of some bigger manifold on which the form
is defined.