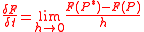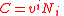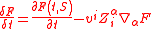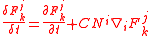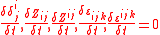Calculus of moving surfaces - AbsoluteAstronomy.com

The calculus of moving surfaces (CMS) is an extension of the classical tensor calculus

Tensor

Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...

to deforming manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

s. Central to the CMS is the

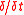-derivative

Derivative

In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...

whose original definition was put forth by Jacques Hadamard

Jacques Hadamard

Jacques Salomon Hadamard FRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.-Biography:...

. It plays the role analogous to that of the covariant derivative

Covariant derivative

In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...

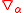on differential manifolds

Differentiable manifold

A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...

. In particular, it has the property that it produces a tensor

Tensor

when applied to a tensor.

Suppose that

is the evolution of the surface

Surface

In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...

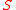indexed by a time-like parameter

. The definitions of the surface velocity

Velocity

In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...

and the operator

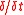are the geometric foundations of the CMS. The velocity C is the rate of deformation of the surface

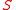in the instantaneous normal

Surface normal

A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...

direction. The value of

at a point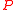

is defined as the limit

Limit of a function

In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....

where

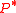is the point on

that lies on the straight line perpendicular to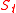

at point P. This definition is illustrated in the first geometric figure below. The velocity

is a signed quantity: it is positive when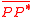

points in the direction of the chosen normal, and negative otherwise. The relationship between

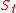and

is analogous to the relationship between location and velocity in elementary calculus: knowing either quantity allows one to construct the other by differentiation

Derivative

or integration

Initial value problem

In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...

.
The

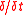-derivative for a scalar field F defined on

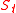is the rate of change

Derivative

in the instantaneously normal direction:

This definition is also illustrated in second geometric figure.

The above definitions are geometric
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

. In analytical settings, direct application of these definitions may not be possible. The CMS gives analytical definitions of C and

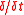in terms of elementary operations from calculus

Calculus

Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...

and differential geometry.

Analytical definitions

For analytical

Mathematical analysis

Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...

definitions of

and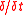

, consider the evolution of

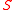given by

where

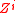are general curvilinear space coordinates

Curvilinear coordinates

Curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given...

and

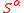are the surface coordinates. By convention, tensor indices of function arguments are dropped. Thus the above equations contains

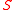rather than

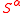.The velocity object

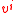is defined as the partial derivative

Partial derivative

In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...

The velocity

can be computed most directly by the formula

where

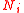are the covariant components of the normal vector

.

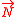The definition of the

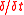-derivative for an invariant

Tensor field

In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...

F reads

where

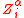is the shift tensor and

is the covariant derivative on S.

For tensors, an appropriate generalization is needed. The proper definition for a representative tensor

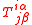reads

where

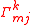are Christoffel symbols

Christoffel symbols

In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...

Properties of the δ/δt-derivative

The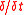

-derivative commutes with contraction, satisfies the product rule

Product rule

In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...

for any collection of indices

and obeys a chain rule

Chain rule

In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...

for surface restrictions of spatial tensors:

Chain rule shows that the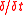

-derivative of spatial "metrics"
vanishes

where

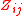and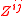

are covariant and contravariant metric tensor

Metric tensor

In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...

is the Kronecker delta symbol, and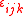

and

are the Levi-Civita symbol

Levi-Civita symbol

The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...

s. The main article

Levi-Civita symbol

The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...

on Levi-Civita symbols describes them for Cartesian coordinate systems. The preceding rule is valid in general coordinates, where the definition of the Levi-Civita symbols must include the square root of the determinant

Determinant

In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

of the covariant metric tensor

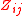Differentiation table for the δ/δt-derivative

The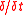

-derivative of the key surface objects leads to highly concise and attractive formulas. When applied to the covariant surface metric tensor

Metric tensor

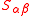and the contravariant metric tensor

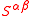, the following identities result

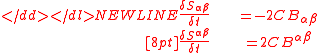
where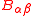

and

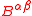are the doubly covariant and doubly contravariant curvature tensors

Sectional curvature

In Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...

. These curvature tensors, as well as for the mixed curvature tensor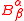

, satisfy

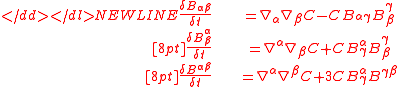
The shift tensor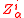

and the normal

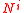satisfy

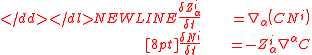
Finally, the surface Levi-Civita symbol

Levi-Civita symbol

The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...

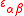and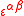

satisfy

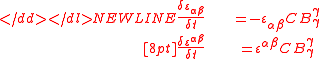
Time differentiation of integrals

The CMS provides rules for time differentiation of volume and surface integrals

Time evolution of integrals

In many applications, one needs to calculate the rate of change of a volume or surface integral whose domain of integration, as well as the integrand, are functions of a particular parameter...

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.