Tensor field
Encyclopedia
In mathematics
, physics
and engineering
, a tensor field assigns a tensor
to each point of a mathematical space (typically a Euclidean space
or manifold
). Tensor fields are used in differential geometry, algebraic geometry
, general relativity
, in the analysis of stress
and strain in materials, and in numerous applications in the physical sciences and engineering. As a tensor is a generalization of a scalar
(a pure number representing a value, like length) and a vector (a geometrical arrow in space), a tensor field is a generalization of a scalar field
or vector field
that assigns, respectively, a scalar or vector to each point of space.
Many mathematical structures informally called 'tensors' are actually 'tensor fields', that is, fields defined over a manifold which define a tensor at every point of the manifold. An example is the Riemann curvature tensor
.
The general idea of tensor field combines the requirement of richer geometry — for example, an ellipsoid varying from point to point, in the case of a metric tensor
— with the idea that we don't want our notion to depend on the particular method of mapping the surface. It should exist independently of latitude and longitude, or whatever particular 'cartographic projection' we are using to introduce numerical co-ordinates.
There is the idea of vector bundle
, which is a natural idea of 'vector space
depending on parameters' — the parameters being in a manifold. For example a vector space of one dimension depending on an angle could look like a Möbius strip
as well as a cylinder
. Given a vector bundle V over M, the corresponding field concept is called a section of the bundle: for m varying over M, a choice of vector
the vector space 'at' m.
Since the tensor product
concept is independent of any choice of basis, taking the tensor product of two vector bundles on M is routine. Starting with the tangent bundle
(the bundle of tangent space
s) the whole apparatus explained at component-free treatment of tensors carries over in a routine way — again independently of co-ordinates, as mentioned in the introduction.
We therefore can give a definition of tensor field, namely as a section
of some tensor bundle
. (There are vector bundles which are not tensor bundles: the Möbius band for instance.) This is then guaranteed geometric content, since everything has been done in an intrinsic way. More precisely, a tensor field assigns to any given point of the manifold a tensor in the space
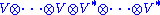
where V is the tangent space
at that point and V* is the cotangent space
. See also tangent bundle
and cotangent bundle
.
Given two tensor bundles E → M and F→M, a map A: Γ(E) → Γ(F) from the space of sections of E to sections of F can be considered itself as a tensor section of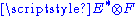
if and only if it satisfies A(fs,...) = fA(s,...) in each argument, where f is a smooth function on M. Thus a tensor is not only a linear map on the vector space of sections, but a C∞(M)-linear map on the module of sections. This property is used to check, for example, that even though the Lie derivative
and covariant derivative
are not tensors, the torsion
and curvature tensors
built from them are.
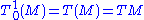
to emphasize that the tangent bundle is the range space of the (1,0) tensor fields (i.e., vector fields) on the manifold M. Do not confuse this with the very similar looking notation
;
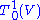in the latter case, we just have one tensor space, whereas in the former, we have a tensor space defined for each point in the manifold M.
Curly (script) letters are sometimes used to denote the set of infinitely-differentiable
tensor fields on M. Thus,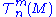
are the sections of the (m,n) tensor bundle on M which are infinitely-differentiable. A tensor field is an element of this set.
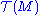(see the section on notation above) as a single space — a module
over the ring
of smooth functions, C∞(M), by pointwise scalar multiplication. The notions of multilinearity and tensor products extend easily to the case of modules over any commutative ring.
As a motivating example, consider the space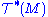
of smooth covector fields (1-forms
), also a module over the smooth functions. These act on smooth vector fields to yield smooth functions by pointwise evaluation, namely, given a covector field ω and a vector field X, we define
)(p) = ω(p)(X(p)).
Because of the pointwise nature of everything involved, the action of ω on X is a C∞(M)-linear map, that is,
)(p) = f(p) ω(p)(X(p)) = (fω)(p)(X(p))
for any p in M and smooth function f. Thus we can regard covector fields not just as sections of the cotangent bundle, but also linear mappings of vector fields into functions. By the double-dual construction, vector fields can similarly be expressed as mappings of covector fields into functions (namely, we could start "natively" with covector fields and work up from there).
In a complete parallel to the construction of ordinary single tensors (not fields!) on M as multilinear maps on vectors and covectors, we can regard general (k,l) tensor fields on M as C∞(M)-multilinear maps defined on l copies of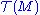
and k copies of 
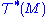into C∞(M).
Now, given any arbitrary mapping T from a product of k copies of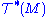
and l copies of 
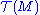into C∞(M), it turns out that it arises from a tensor field on M if and only if it is a multilinear over C∞(M). Thus this kind of multilinearity implicitly expresses the fact that we're really dealing with a pointwise-defined object, i.e. a tensor field, as opposed to a function which, even when evaluated at a single point, depends on all the values of vector fields and 1-forms simultaneously.
A frequent example application of this general rule is showing that the Levi-Civita connection
, which is a mapping of smooth vector fields
taking a pair of vector fields to a vector field, does not define a tensor field on M. This is because it is only R-linear in Y (in place of full C∞(M)-linearity, it satisfies the Leibniz rule, 
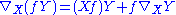)). Nevertheless it must be stressed that even though it is not a tensor field, it still qualifies as a geometric object with a component-free interpretation.
is important in physics and engineering. Both of these are related by Einstein's theory of general relativity
. In engineering, the underlying manifold will often be Euclidean 3-space
.
It is worth noting that differential form
s, used in defining integration on manifolds, are a type of tensor field.
and other fields, differential equation
s posed in terms of tensor fields provide a very general way to express relationships that are both geometric in nature (guaranteed by the tensor nature) and conventionally linked to differential calculus
. Even to formulate such equations requires a fresh notion, the covariant derivative
. This handles the formulation of variation of a tensor field along a vector field
. The original absolute differential calculus notion, which was later called tensor calculus, led to the isolation of the geometric concept of connection.
L on M. If W is the tensor product bundle of V with L, then W is a bundle of vector spaces of just the same dimension as V. This allows one to define the concept of tensor density, a 'twisted' type of tensor field. A tensor density is the special case where L is the bundle of densities on a manifold, namely the determinant bundle of the cotangent bundle
. (To be strictly accurate, one should also apply the absolute value
to the transition functions
— this makes little difference for an orientable manifold.) For a more traditional explanation see the tensor density
article.
One feature of the bundle of densities (again assuming orientability) L is that Ls is well-defined for real number values of s; this can be read from the transition functions, which take strictly positive real values. This means for example that we can take a half-density, the case where s = ½. In general we can take sections of W, the tensor product of V with Ls, and consider tensor density fields with weight s.
Half-densities are applied in areas such as defining integral operators on manifolds, and geometric quantization
.
and all the fields are taken to be invariant by translations
by the vectors of M, we get back to a situation where a tensor field is synonymous with a tensor 'sitting at the origin'. This does no great harm, and is often used in applications. As applied to tensor densities, it does make a difference. The bundle of densities cannot seriously be defined 'at a point'; and therefore a limitation of the contemporary mathematical treatment of tensors is that tensor densities are defined in a roundabout fashion.
in the multivariable case, as applied to coordinate changes, also as the requirement for self-consistent concepts of tensor giving rise to tensor fields.
Abstractly, we can identify the chain rule as a 1-cocycle
. It gives the consistency required to define the tangent bundle in an intrinsic way. The other vector bundles of tensors have comparable cocycles, which come from applying functorial properties of tensor constructions to the chain rule itself; this is why they also are intrinsic (read, 'natural') concepts.
What is usually spoken of as the 'classical' approach to tensors tries to read this backwards — and is therefore a heuristic, post hoc approach rather than truly a foundational one. Implicit in defining tensors by how they transform under a coordinate change is the kind of self-consistency the cocycle expresses. The construction of tensor densities is a 'twisting' at the cocycle level. Geometers have not been in any doubt about the geometric nature of tensor quantities; this kind of descent
argument justifies abstractly the whole theory.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, a tensor field assigns a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
to each point of a mathematical space (typically a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
or manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
). Tensor fields are used in differential geometry, algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, in the analysis of stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
and strain in materials, and in numerous applications in the physical sciences and engineering. As a tensor is a generalization of a scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
(a pure number representing a value, like length) and a vector (a geometrical arrow in space), a tensor field is a generalization of a scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
or vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
that assigns, respectively, a scalar or vector to each point of space.
Many mathematical structures informally called 'tensors' are actually 'tensor fields', that is, fields defined over a manifold which define a tensor at every point of the manifold. An example is the Riemann curvature tensor
Riemann curvature tensor
In the mathematical field of differential geometry, the Riemann curvature tensor, or Riemann–Christoffel tensor after Bernhard Riemann and Elwin Bruno Christoffel, is the most standard way to express curvature of Riemannian manifolds...
.
Geometric introduction
Intuitively, a vector field is best visualized as an 'arrow' attached to each point of a region, with variable length and direction. One example of a vector field on a curved space is a weather map showing horizontal wind velocity at each point of the Earth's surface.The general idea of tensor field combines the requirement of richer geometry — for example, an ellipsoid varying from point to point, in the case of a metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
— with the idea that we don't want our notion to depend on the particular method of mapping the surface. It should exist independently of latitude and longitude, or whatever particular 'cartographic projection' we are using to introduce numerical co-ordinates.
The vector bundle explanation
The contemporary mathematical expression of the idea of tensor field breaks it down into a two-step concept.There is the idea of vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
, which is a natural idea of 'vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
depending on parameters' — the parameters being in a manifold. For example a vector space of one dimension depending on an angle could look like a Möbius strip
Möbius strip
The Möbius strip or Möbius band is a surface with only one side and only one boundary component. The Möbius strip has the mathematical property of being non-orientable. It can be realized as a ruled surface...
as well as a cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
. Given a vector bundle V over M, the corresponding field concept is called a section of the bundle: for m varying over M, a choice of vector
- vm in Vm,
the vector space 'at' m.
Since the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
concept is independent of any choice of basis, taking the tensor product of two vector bundles on M is routine. Starting with the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
(the bundle of tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
s) the whole apparatus explained at component-free treatment of tensors carries over in a routine way — again independently of co-ordinates, as mentioned in the introduction.
We therefore can give a definition of tensor field, namely as a section
Section (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
of some tensor bundle
Tensor bundle
In mathematics, the tensor bundle of a manifold is the direct sum of all tensor products of the tangent bundle and the cotangent bundle of that manifold. To do calculus on the tensor bundle a connection is needed....
. (There are vector bundles which are not tensor bundles: the Möbius band for instance.) This is then guaranteed geometric content, since everything has been done in an intrinsic way. More precisely, a tensor field assigns to any given point of the manifold a tensor in the space
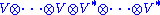
where V is the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
at that point and V* is the cotangent space
Cotangent space
In differential geometry, one can attach to every point x of a smooth manifold a vector space called the cotangent space at x. Typically, the cotangent space is defined as the dual space of the tangent space at x, although there are more direct definitions...
. See also tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
and cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
.
Given two tensor bundles E → M and F→M, a map A: Γ(E) → Γ(F) from the space of sections of E to sections of F can be considered itself as a tensor section of
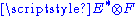if and only if it satisfies A(fs,...) = fA(s,...) in each argument, where f is a smooth function on M. Thus a tensor is not only a linear map on the vector space of sections, but a C∞(M)-linear map on the module of sections. This property is used to check, for example, that even though the Lie derivativeLie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
and covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
are not tensors, the torsion
Torsion tensor
In differential geometry, the notion of torsion is a manner of characterizing a twist or screw of a moving frame around a curve. The torsion of a curve, as it appears in the Frenet-Serret formulas, for instance, quantifies the twist of a curve about its tangent vector as the curve evolves In the...
and curvature tensors
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
built from them are.
Notation
The notation for tensor fields can sometimes be confusingly similar to the notation for tensor spaces. Thus, the tangent bundle TM = T(M) might sometimes be written as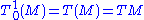to emphasize that the tangent bundle is the range space of the (1,0) tensor fields (i.e., vector fields) on the manifold M. Do not confuse this with the very similar looking notation
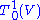;in the latter case, we just have one tensor space, whereas in the former, we have a tensor space defined for each point in the manifold M.
Curly (script) letters are sometimes used to denote the set of infinitely-differentiable
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
tensor fields on M. Thus,
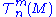
are the sections of the (m,n) tensor bundle on M which are infinitely-differentiable. A tensor field is an element of this set.
The C∞(M) module explanation
There is another more abstract (but often useful) way of characterizing tensor fields on a manifold M which turns out to actually make tensor fields into honest tensors (i.e. single multilinear mappings), though of a different type (and this is not usually why one often says "tensor" when one really means "tensor field"). First, we may consider the set of all smooth (C∞) vector fields on M,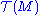 (see the section on notation above) as a single space — a moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of smooth functions, C∞(M), by pointwise scalar multiplication. The notions of multilinearity and tensor products extend easily to the case of modules over any commutative ring.
As a motivating example, consider the space
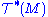of smooth covector fields (1-formsDifferential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
), also a module over the smooth functions. These act on smooth vector fields to yield smooth functions by pointwise evaluation, namely, given a covector field ω and a vector field X, we define
)(p) = ω(p)(X(p)).
Because of the pointwise nature of everything involved, the action of ω on X is a C∞(M)-linear map, that is,
)(p) = f(p) ω(p)(X(p)) = (fω)(p)(X(p))
for any p in M and smooth function f. Thus we can regard covector fields not just as sections of the cotangent bundle, but also linear mappings of vector fields into functions. By the double-dual construction, vector fields can similarly be expressed as mappings of covector fields into functions (namely, we could start "natively" with covector fields and work up from there).
In a complete parallel to the construction of ordinary single tensors (not fields!) on M as multilinear maps on vectors and covectors, we can regard general (k,l) tensor fields on M as C∞(M)-multilinear maps defined on l copies of
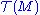and k copies of 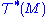into C∞(M).Now, given any arbitrary mapping T from a product of k copies of
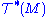and l copies of 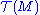into C∞(M), it turns out that it arises from a tensor field on M if and only if it is a multilinear over C∞(M). Thus this kind of multilinearity implicitly expresses the fact that we're really dealing with a pointwise-defined object, i.e. a tensor field, as opposed to a function which, even when evaluated at a single point, depends on all the values of vector fields and 1-forms simultaneously.A frequent example application of this general rule is showing that the Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
, which is a mapping of smooth vector fields
taking a pair of vector fields to a vector field, does not define a tensor field on M. This is because it is only R-linear in Y (in place of full C∞(M)-linearity, it satisfies the Leibniz rule, 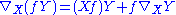)). Nevertheless it must be stressed that even though it is not a tensor field, it still qualifies as a geometric object with a component-free interpretation.Applications
The curvature tensor is discussed in differential geometry and the stress-energy tensorStress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
is important in physics and engineering. Both of these are related by Einstein's theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. In engineering, the underlying manifold will often be Euclidean 3-space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
It is worth noting that differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s, used in defining integration on manifolds, are a type of tensor field.
Tensor calculus
In theoretical physicsTheoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
and other fields, differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s posed in terms of tensor fields provide a very general way to express relationships that are both geometric in nature (guaranteed by the tensor nature) and conventionally linked to differential calculus
Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
. Even to formulate such equations requires a fresh notion, the covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
. This handles the formulation of variation of a tensor field along a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
. The original absolute differential calculus notion, which was later called tensor calculus, led to the isolation of the geometric concept of connection.
Twisting by a line bundle
An extension of the tensor field idea incorporates an extra line bundleLine bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
L on M. If W is the tensor product bundle of V with L, then W is a bundle of vector spaces of just the same dimension as V. This allows one to define the concept of tensor density, a 'twisted' type of tensor field. A tensor density is the special case where L is the bundle of densities on a manifold, namely the determinant bundle of the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
. (To be strictly accurate, one should also apply the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
to the transition functions
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
— this makes little difference for an orientable manifold.) For a more traditional explanation see the tensor density
Tensor density
In differential geometry, a tensor density or relative tensor is a generalization of the tensor concept. A tensor density transforms as a tensor when passing from one coordinate system to another , except that it is additionally multiplied or weighted by a power of the Jacobian determinant of the...
article.
One feature of the bundle of densities (again assuming orientability) L is that Ls is well-defined for real number values of s; this can be read from the transition functions, which take strictly positive real values. This means for example that we can take a half-density, the case where s = ½. In general we can take sections of W, the tensor product of V with Ls, and consider tensor density fields with weight s.
Half-densities are applied in areas such as defining integral operators on manifolds, and geometric quantization
Geometric quantization
In mathematical physics, geometric quantization is a mathematical approach to defining a quantum theory corresponding to a given classical theory. It attempts to carry out quantization, for which there is in general no exact recipe, in such a way that certain analogies between the classical theory...
.
The flat case
When M is a Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
and all the fields are taken to be invariant by translations
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
by the vectors of M, we get back to a situation where a tensor field is synonymous with a tensor 'sitting at the origin'. This does no great harm, and is often used in applications. As applied to tensor densities, it does make a difference. The bundle of densities cannot seriously be defined 'at a point'; and therefore a limitation of the contemporary mathematical treatment of tensors is that tensor densities are defined in a roundabout fashion.
Cocycles and chain rules
As an advanced explanation of the tensor concept, one can interpret the chain ruleChain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
in the multivariable case, as applied to coordinate changes, also as the requirement for self-consistent concepts of tensor giving rise to tensor fields.
Abstractly, we can identify the chain rule as a 1-cocycle
Cocycle
A cocycle refers to any one of the following:*A closed cochain in algebraic topology is called a cocycle.*A particular type of map in an autonomous dynamical system; see Oseledec theorem....
. It gives the consistency required to define the tangent bundle in an intrinsic way. The other vector bundles of tensors have comparable cocycles, which come from applying functorial properties of tensor constructions to the chain rule itself; this is why they also are intrinsic (read, 'natural') concepts.
What is usually spoken of as the 'classical' approach to tensors tries to read this backwards — and is therefore a heuristic, post hoc approach rather than truly a foundational one. Implicit in defining tensors by how they transform under a coordinate change is the kind of self-consistency the cocycle expresses. The construction of tensor densities is a 'twisting' at the cocycle level. Geometers have not been in any doubt about the geometric nature of tensor quantities; this kind of descent
Descent (category theory)
In mathematics, the idea of descent has come to stand for a very general idea, extending the intuitive idea of 'gluing' in topology. Since the topologists' glue is actually the use of equivalence relations on topological spaces, the theory starts with some ideas on identification.A sophisticated...
argument justifies abstractly the whole theory.