Geometric quantization
Encyclopedia
In mathematical physics
, geometric quantization is a mathematical approach to defining a quantum theory
corresponding to a given classical theory. It attempts to carry out quantization
, for which there is in general no exact recipe, in such a way that certain analogies between the classical theory and the quantum theory remain manifest. For example, the similarity between the Heisenberg equation in the Heisenberg picture
of quantum mechanics
and the Hamilton equation in classical physics should be built in.
One of the earliest attempts at a natural quantization was Weyl quantization
, proposed by Hermann Weyl
in 1927. Here, an attempt is made to associate a quantum-mechanical observable (a self-adjoint operator
on a Hilbert space
) with a real-valued function on classical phase space
. Here, the position and momentum are reinterpreted as the generators of the Heisenberg group, and the Hilbert space appears as a group representation
of the Heisenberg group. In 1946,
H. J. Groenewold
(H.J. Groenewold, "On the Principles of elementary quantum mechanics", Physica,12 (1946) pp. 405-460) considered the product of a pair of such observables and asked what the corresponding function would be on the classical phase space. This led him to define the phase-space star-product
of a pair of functions. More generally, this technique leads to deformation quantization, where the ∗-product is taken to be a deformation of the algebra of functions on a symplectic manifold
or Poisson manifold
. However, as a natural quantization scheme, Weyl's map is not satisfactory.
For example, the Weyl map of the classical angular-momentum-squared is not just the quantum angular momentum squared
operator, but it further contains a constant term 3ħ2/2. This extra term is actually physically significant, since it accounts for the nonvanishing angular momentum of the ground-state Bohr orbit in the hydrogen atom.
The geometric quantization procedure falls into the following three steps: prequantization, polarization, and metaplectic correction.
where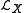
is the Lie derivative of a half-form with respect to a vector field X.
Geometric quantization of Poisson manifolds and symplectic foliations also is developed. For instance, this is the case of partially integrable
and superintegrable
Hamiltonian systems and non-autonomous mechanics
.
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, geometric quantization is a mathematical approach to defining a quantum theory
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
corresponding to a given classical theory. It attempts to carry out quantization
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
, for which there is in general no exact recipe, in such a way that certain analogies between the classical theory and the quantum theory remain manifest. For example, the similarity between the Heisenberg equation in the Heisenberg picture
Heisenberg picture
In physics, the Heisenberg picture is a formulation of quantum mechanics in which the operators incorporate a dependency on time, but the state vectors are time-independent. It stands in contrast to the Schrödinger picture in which the operators are constant and the states evolve in time...
of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and the Hamilton equation in classical physics should be built in.
One of the earliest attempts at a natural quantization was Weyl quantization
Weyl quantization
In mathematics and physics, in the area of quantum mechanics, Weyl quantization is a method for systematically associating a "quantum mechanical" Hermitian operator with a "classical" kernel function in phase space invertibly...
, proposed by Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
in 1927. Here, an attempt is made to associate a quantum-mechanical observable (a self-adjoint operator
Self-adjoint operator
In mathematics, on a finite-dimensional inner product space, a self-adjoint operator is an operator that is its own adjoint, or, equivalently, one whose matrix is Hermitian, where a Hermitian matrix is one which is equal to its own conjugate transpose...
on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
) with a real-valued function on classical phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
. Here, the position and momentum are reinterpreted as the generators of the Heisenberg group, and the Hilbert space appears as a group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the Heisenberg group. In 1946,
H. J. Groenewold
Hilbrand J. Groenewold
Hilbrand Johannes Groenewold was a Dutch theoretical physicist who pioneered the largely operator-free formulation of quantum mechanics in phase space known as phase-space quantization....
(H.J. Groenewold, "On the Principles of elementary quantum mechanics", Physica,12 (1946) pp. 405-460) considered the product of a pair of such observables and asked what the corresponding function would be on the classical phase space. This led him to define the phase-space star-product
Moyal product
In mathematics, the Moyal product, named after José Enrique Moyal, is perhaps the best-known example of a phase-space star product: an associative, non-commutative product, ∗, on the functions on ℝ2n, equipped with its Poisson bracket .This particular star product is also sometimes called...
of a pair of functions. More generally, this technique leads to deformation quantization, where the ∗-product is taken to be a deformation of the algebra of functions on a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
or Poisson manifold
Poisson manifold
In mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
. However, as a natural quantization scheme, Weyl's map is not satisfactory.
For example, the Weyl map of the classical angular-momentum-squared is not just the quantum angular momentum squared
operator, but it further contains a constant term 3ħ2/2. This extra term is actually physically significant, since it accounts for the nonvanishing angular momentum of the ground-state Bohr orbit in the hydrogen atom.
The geometric quantization procedure falls into the following three steps: prequantization, polarization, and metaplectic correction.
- Prequantization of a symplectic manifold
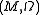provides a representation of elements 
of the Poisson algebraPoisson algebraIn mathematics, a Poisson algebra is an associative algebra together with a Lie bracket that also satisfies Leibniz' law; that is, the bracket is also a derivation. Poisson algebras appear naturally in Hamiltonian mechanics, and are also central in the study of quantum groups...
of smooth real functions on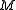
by first order differential operators 
on sections of a complex line bundleFiber bundleIn mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
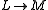. In accordance with the Kostant - Souriau prequantization formula, these operators are expressed via a connectionConnection (mathematics)In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
on
whose curvature formCurvature formIn differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
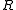obeys the prequantization condition 
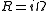. - By polarization is meant an integrable maximal distributionDistribution (differential geometry)In differential geometry, a discipline within mathematics, a distribution is a subset of the tangent bundle of a manifold satisfying certain properties...
on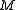 
such that 
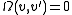for all 
. Integrable means 
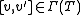for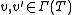 
(sections of T). The quantum algebra 
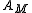of a symplectic manifold 
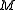consists of the operators 
of functions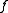 
whose Hamiltonian vector fieldHamiltonian vector fieldIn mathematics and physics, a Hamiltonian vector field on a symplectic manifold is a vector field, defined for any energy function or Hamiltonian. Named after the physicist and mathematician Sir William Rowan Hamilton, a Hamiltonian vector field is a geometric manifestation of Hamilton's equations...
s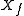
satisfiy the condition 
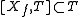. - In accordance with the metaplectic correction, elements of the quantum algebra
act in the pre-Hilbert spaceInner product spaceIn mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
of half-forms with values in the prequantization Line bundle on a symplectic manifold
. The quantization is simply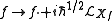
where
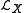is the Lie derivative of a half-form with respect to a vector field X.Geometric quantization of Poisson manifolds and symplectic foliations also is developed. For instance, this is the case of partially integrable
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
and superintegrable
Superintegrable Hamiltonian system
In mathematics, a superintegrable Hamiltonian system is a Hamiltonian system on a 2n-dimensional symplectic manifold for which the following conditions hold: There exist n ≤ k independent integrals F i of motion...
Hamiltonian systems and non-autonomous mechanics
Non-autonomous mechanics
Non-autonomous mechanics describe non-relativistic mechanical systems subject to time-dependent transformations. In particular, this is the case of mechanical systems whose Lagrangians and Hamiltonians depend on the time. The configuration space of non-autonomous mechanics isa fiber bundle Q\to...
.
External links
- William Ritter's review of Geometric Quantization presents a general framework for all problems in physicsPhysicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and fits geometric quantization into this framework - John Baez's review of Geometric Quantization, by John Baez is short and pedagogical
- Matthias Blau's primer on Geometric Quantization, one of the very few good primers (ps format only)
- A. Echeverria-Enriquez, M. Munoz-Lecanda, N. Roman-Roy, Mathematical foundations of geometric quantization, arXiv: math-ph/9904008.
- G. SardanashvilyGennadi SardanashvilyGennadi Sardanashvily is a theoretical physicist, a principal research scientist of Moscow State University.- Biography :...
, Geometric quantization of symplectic foliations, arXiv: math-ph/0110196.