Poisson manifold
Encyclopedia
In mathematics
, a Poisson manifold is a differentiable manifold
M such that the algebra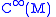
of smooth function
s over M is equipped with a bilinear map called the Poisson bracket
, turning it into a Poisson algebra
. Since their introduction by André Lichnerowicz
in 1977, Poisson
geometry and the cohomology of Poisson manifolds have developed into a wide field of research.
Every symplectic manifold
is a Poisson manifold but not vice versa.
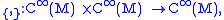
such that the bracket is skew symmetric:
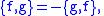
obeys the Jacobi identity
:
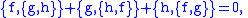
and is a derivation
of C∞(M) in its first argument:
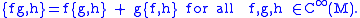
The last property allows several equivalent formulations. Fixing a smooth function g ∈ C∞(M), one has that the map f ↦ {f, g} is a derivation on C∞(M). This implies the existence of a Hamiltonian vector field
Xg on M such that
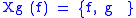
for all f ∈ C∞(M). This implies that the bracket depends only on the differential of f. Thus, associated with any Poisson structure is a map from the cotangent bundle
T∗M to the tangent bundle
TM,
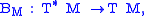
which maps df to Xf.
field η on M, the Poisson bivector, a skew-symmetric 2-tensor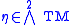
, such that
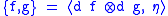
where
is the pairing between the tangent bundle and its dual. Conversely, given a smooth bivector field η on M, this formula can be used to define a skew-symmetric bracket which is a derivation in each argument. This bracket obeys the Jacobi identity, and hence defines a Poisson structure if and only if the Schouten–Nijenhuis bracket [η,η] is zero.
In local coordinates, the bivector at a point x = (x1, ..., xm) has the expression
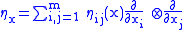
so that
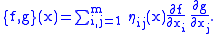
For a symplectic manifold, η is nothing other than the pairing between tangent and cotangent bundle induced by the symplectic form ω, which exists because it is nondegenerate. The difference between a symplectic manifold and a Poisson manifold is that the symplectic form must be nowhere singular, whereas the Poisson bivector does not need to be of full rank everywhere. When the Poisson bivector is zero everywhere, the manifold is said to possess the trivial Poisson structure.
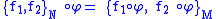
where { , }M and { , }N are the Poisson brackets on M and N respectively.
may be defined on the product manifold. Letting f1 and f2 be two smooth function
s defined on the product manifold M × N, one defines the Poisson bracket { , }M×N on the product manifold in terms of the brackets { , }M and { , }N on each of the individual manifolds:
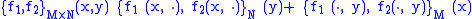
where x ∈ M and y ∈ N are held constant; that is, so that when
then
and
is implied.
of a Hamiltonian vector field. That is, the relation "piecewise connected by integral curves of Hamiltonian fields" is an equivalence relation
on the manifold. The equivalence classes of this relation are the symplectic leaves.
is a finite-dimensional Lie algebra
, and
is its dual vector space, then the Lie bracket induces a Poisson structure on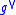 
.
More precisely, we identify the cotangent bundle
of the manifold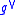
, ie the dual of 
to the Lie algebra 
. Then for two functions f1 and f2 on 
, and a point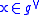 
, one may define
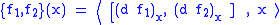
where the Lie bracket [ , ] is computed in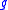
through the isomorphism:
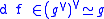
If ek are the local coordinates on the Lie algebra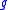
, then the Poisson bivector is given by
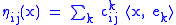
where the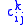
are the structure constants of the Lie algebra.
The symplectic leaves of this Poisson algebra are the coadjoint orbits of the Lie algebra used for the orbit method.
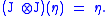
The symplectic leaves of a complex Poisson manifold are pseudo-Kähler manifolds.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Poisson manifold is a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
M such that the algebra
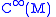of smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s over M is equipped with a bilinear map called the Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
, turning it into a Poisson algebra
Poisson algebra
In mathematics, a Poisson algebra is an associative algebra together with a Lie bracket that also satisfies Leibniz' law; that is, the bracket is also a derivation. Poisson algebras appear naturally in Hamiltonian mechanics, and are also central in the study of quantum groups...
. Since their introduction by André Lichnerowicz
André Lichnerowicz
André Lichnerowicz was a noted French differential geometer and mathematical physicist of Polish descent.-Biography:...
in 1977, Poisson
geometry and the cohomology of Poisson manifolds have developed into a wide field of research.
Every symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
is a Poisson manifold but not vice versa.
Definition
A Poisson structure on M is a bilinear map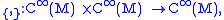such that the bracket is skew symmetric:
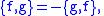
obeys the Jacobi identity
Jacobi identity
In mathematics the Jacobi identity is a property that a binary operation can satisfy which determines how the order of evaluation behaves for the given operation. Unlike for associative operations, order of evaluation is significant for operations satisfying Jacobi identity...
:
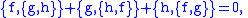
and is a derivation
Derivation
Derivation may refer to:* Derivation , a function on an algebra which generalizes certain features of the derivative operator* Derivation * Derivation in differential algebra, a unary function satisfying the Leibniz product law...
of C∞(M) in its first argument:
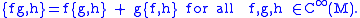
The last property allows several equivalent formulations. Fixing a smooth function g ∈ C∞(M), one has that the map f ↦ {f, g} is a derivation on C∞(M). This implies the existence of a Hamiltonian vector field
Hamiltonian vector field
In mathematics and physics, a Hamiltonian vector field on a symplectic manifold is a vector field, defined for any energy function or Hamiltonian. Named after the physicist and mathematician Sir William Rowan Hamilton, a Hamiltonian vector field is a geometric manifestation of Hamilton's equations...
Xg on M such that
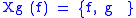
for all f ∈ C∞(M). This implies that the bracket depends only on the differential of f. Thus, associated with any Poisson structure is a map from the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
T∗M to the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
TM,
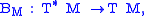
which maps df to Xf.
Poisson bivector
The map between the cotangent and tangent bundles implies the existence of a bivectorBivector
In mathematics, a bivector or 2-vector is a quantity in geometric algebra or exterior algebra that generalises the idea of a vector. If a scalar is considered a zero dimensional quantity, and a vector is a one dimensional quantity, then a bivector can be thought of as two dimensional. Bivectors...
field η on M, the Poisson bivector, a skew-symmetric 2-tensor
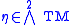, such that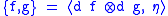where
is the pairing between the tangent bundle and its dual. Conversely, given a smooth bivector field η on M, this formula can be used to define a skew-symmetric bracket which is a derivation in each argument. This bracket obeys the Jacobi identity, and hence defines a Poisson structure if and only if the Schouten–Nijenhuis bracket [η,η] is zero.In local coordinates, the bivector at a point x = (x1, ..., xm) has the expression
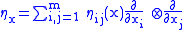
so that
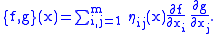
For a symplectic manifold, η is nothing other than the pairing between tangent and cotangent bundle induced by the symplectic form ω, which exists because it is nondegenerate. The difference between a symplectic manifold and a Poisson manifold is that the symplectic form must be nowhere singular, whereas the Poisson bivector does not need to be of full rank everywhere. When the Poisson bivector is zero everywhere, the manifold is said to possess the trivial Poisson structure.
Poisson map
A Poisson map is defined as a smooth map φ: M → N, which maps the Poisson manifold M to the Poisson manifold N, in such a way that the product structure is preserved: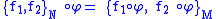where { , }M and { , }N are the Poisson brackets on M and N respectively.
Product manifold
Given two Poisson manifolds M and N, a Poisson bracketPoisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
may be defined on the product manifold. Letting f1 and f2 be two smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s defined on the product manifold M × N, one defines the Poisson bracket { , }M×N on the product manifold in terms of the brackets { , }M and { , }N on each of the individual manifolds:
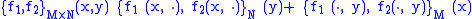
where x ∈ M and y ∈ N are held constant; that is, so that when
then
and
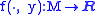
is implied.
Symplectic leaves
A Poisson manifold can be split into a collection of symplectic leaves. Each leaf is a submanifold of the Poisson manifold, and each leaf is a symplectic manifold itself. Two points lie in the same leaf if they are joined by a piecewise smooth curve, where each piece is the integral curveIntegral curve
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
of a Hamiltonian vector field. That is, the relation "piecewise connected by integral curves of Hamiltonian fields" is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
on the manifold. The equivalence classes of this relation are the symplectic leaves.
Example
If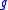 is a finite-dimensional Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
, and
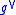is its dual vector space, then the Lie bracket induces a Poisson structure on 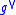.More precisely, we identify the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of the manifold
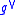, ie the dual of to the Lie algebra . Then for two functions f1 and f2 on , and a point 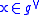, one may define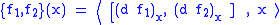where the Lie bracket [ , ] is computed in
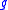through the isomorphism: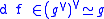If ek are the local coordinates on the Lie algebra
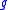, then the Poisson bivector is given by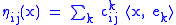where the
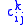are the structure constants of the Lie algebra.The symplectic leaves of this Poisson algebra are the coadjoint orbits of the Lie algebra used for the orbit method.
Complex structure
A complex Poisson manifold is a Poisson manifold with a complex or almost complex structure J such that the complex structure preserves the bivector: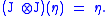The symplectic leaves of a complex Poisson manifold are pseudo-Kähler manifolds.