
Symplectic manifold
Encyclopedia
In mathematics
, a symplectic manifold is a smooth manifold, M, equipped with a closed
nondegenerate differential 2-form
, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology
. Symplectic manifolds arise naturally in abstract formulations of classical mechanics
and analytical mechanics
as the cotangent bundle
s of manifolds, e.g., in the Hamiltonian formulation
of classical mechanics, which provides one of the major motivations for the field: The set of all possible configurations of a system is modelled as a manifold, and this manifold's cotangent bundle describes the phase space
of the system.
Any real-valued differentiable function, H, on a symplectic manifold can serve as an energy function or Hamiltonian. Associated to any Hamiltonian is a Hamiltonian vector field
; the integral curve
s of the Hamiltonian vector field are solutions to Hamilton's equations. The Hamiltonian vector field defines a flow on the symplectic manifold, called a Hamiltonian flow or symplectomorphism
. By Liouville's theorem
, Hamiltonian flows preserve the volume form
on the phase space.
ω. The non-degeneracy condition means that for all we have the property that there does not exist non-zero such that for all The skew-symmetric condition means that for all we have for all Recall that in odd dimensions antisymmetric matrices are not invertible. Since ω is a differential two-form the skew-symmetric condition implies that M has even dimension. The closed condition means that the exterior derivative
of ω, namely dω, is identically zero. A symplectic manifold consists a pair (M,ω), of a manifold M and a symplectic form ω. Assigning a symplectic form ω to a manifold M is referred to as giving M a symplectic structure.
R2n. Let R2n have the basis {v1, ... ,v2n}. Then we define our symplectic form ω so that for all we have and ω is zero for all other pairs of basis vectors. In this case the symplectic form reduces to a simple quadratic form
. If In denotes the identity matrix
then the matrix, Ω, of this quadratic form is given by the block matrix
:

of a symplectic manifold.
The most important case of the isotropic submanifolds is that of Lagrangian submanifolds. A Lagrangian submanifold is, by definition, an isotropic submanifold of maximal dimension, namely half the dimension of the ambient symplectic manifold. Lagrangian submanifolds arise naturally in many physical and geometric situations. One major example is that the graph of a symplectomorphism
in the product symplectic manifold is Lagrangian. Their intersections display rigidity properties not possessed by smooth manifolds; the Arnold conjecture gives the sum of the submanifold's Betti numbers as a lower bound for the number of self intersections of a smooth Lagrangian submanifold, rather than the Euler characteristic in the smooth case.
Lagrangian submanifolds arise naturally in many physical and geometric situations. We shall see below that caustics
can be explained in terms of Lagrangian submanifolds.
where all of the fibres are Lagrangian submanifolds. Since M is even dimensional we can take local coordinates and by Darboux's theorem
the symplectic form ω can be, at least locally, written as , where d denotes the exterior derivative
and ∧ denotes the exterior product. Using this set-up we can locally think of M as being the cotangent bundle
T*Rn, and the Lagrangian fibration as the trivial fibration This is the canonical picture.
of π ○ i is called a caustic
.
Two Lagrangian maps and are called Lagrangian equivalent if there exist diffeomorphisms σ, τ and ν such that both sides of the diagram given on the right commute, and τ preserves the symplectic form. Symbolically: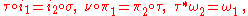
where τ*ω2 denotes the pull back of ω2 by τ.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a symplectic manifold is a smooth manifold, M, equipped with a closed
Closed and exact differential forms
In mathematics, especially vector calculus and differential topology, a closed form is a differential form α whose exterior derivative is zero , and an exact form is a differential form that is the exterior derivative of another differential form β...
nondegenerate differential 2-form
Two-form
In linear algebra, a two-form is another term for a bilinear form, typically used in informal discussions, or sometimes to indicate that the bilinear form is skew-symmetric....
, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology
Symplectic topology
Symplectic geometry is a branch of differential geometry and differential topology which studies symplectic manifolds; that is, differentiable manifolds equipped with a closed, nondegenerate 2-form...
. Symplectic manifolds arise naturally in abstract formulations of classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
and analytical mechanics
Analytical mechanics
Analytical mechanics is a term used for a refined, mathematical form of classical mechanics, constructed from the 18th century onwards as a formulation of the subject as founded by Isaac Newton. Often the term vectorial mechanics is applied to the form based on Newton's work, to contrast it with...
as the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
s of manifolds, e.g., in the Hamiltonian formulation
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
of classical mechanics, which provides one of the major motivations for the field: The set of all possible configurations of a system is modelled as a manifold, and this manifold's cotangent bundle describes the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
of the system.
Any real-valued differentiable function, H, on a symplectic manifold can serve as an energy function or Hamiltonian. Associated to any Hamiltonian is a Hamiltonian vector field
Hamiltonian vector field
In mathematics and physics, a Hamiltonian vector field on a symplectic manifold is a vector field, defined for any energy function or Hamiltonian. Named after the physicist and mathematician Sir William Rowan Hamilton, a Hamiltonian vector field is a geometric manifestation of Hamilton's equations...
; the integral curve
Integral curve
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
s of the Hamiltonian vector field are solutions to Hamilton's equations. The Hamiltonian vector field defines a flow on the symplectic manifold, called a Hamiltonian flow or symplectomorphism
Symplectomorphism
In mathematics, a symplectomorphism is an isomorphism in the category of symplectic manifolds.-Formal definition:A diffeomorphism between two symplectic manifolds f: \rightarrow is called symplectomorphism, iff^*\omega'=\omega,...
. By Liouville's theorem
Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
, Hamiltonian flows preserve the volume form
Volume form
In mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
on the phase space.
Definition
A symplectic form on a manifold M is a closed non-degenerate differential 2-formTwo-form
In linear algebra, a two-form is another term for a bilinear form, typically used in informal discussions, or sometimes to indicate that the bilinear form is skew-symmetric....
ω. The non-degeneracy condition means that for all we have the property that there does not exist non-zero such that for all The skew-symmetric condition means that for all we have for all Recall that in odd dimensions antisymmetric matrices are not invertible. Since ω is a differential two-form the skew-symmetric condition implies that M has even dimension. The closed condition means that the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
of ω, namely dω, is identically zero. A symplectic manifold consists a pair (M,ω), of a manifold M and a symplectic form ω. Assigning a symplectic form ω to a manifold M is referred to as giving M a symplectic structure.
Linear symplectic manifold
There is a standard linear model, namely a symplectic vector spaceSymplectic vector space
In mathematics, a symplectic vector space is a vector space V equipped with a bilinear form ω : V × V → R that is...
R2n. Let R2n have the basis {v1, ... ,v2n}. Then we define our symplectic form ω so that for all we have and ω is zero for all other pairs of basis vectors. In this case the symplectic form reduces to a simple quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
. If In denotes the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
then the matrix, Ω, of this quadratic form is given by the block matrix
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
:

Lagrangian and other submanifolds
There are several natural geometric notions of submanifoldSubmanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
of a symplectic manifold.
- symplectic submanifolds (potentially of any even dimension) are submanifolds where the symplectic form is required to induce a symplectic form on them.
- isotropic submanifolds are submanifolds where the symplectic form restricts to zero, i.e. each tangent space is an isotropic subspace of the ambient manifold's tangent space. Similarly, if each tangent subspace to a submanifold is co-isotropic (the dual of an isotropic subspace), the submanifold is called co-isotropic.
The most important case of the isotropic submanifolds is that of Lagrangian submanifolds. A Lagrangian submanifold is, by definition, an isotropic submanifold of maximal dimension, namely half the dimension of the ambient symplectic manifold. Lagrangian submanifolds arise naturally in many physical and geometric situations. One major example is that the graph of a symplectomorphism
Symplectomorphism
In mathematics, a symplectomorphism is an isomorphism in the category of symplectic manifolds.-Formal definition:A diffeomorphism between two symplectic manifolds f: \rightarrow is called symplectomorphism, iff^*\omega'=\omega,...
in the product symplectic manifold is Lagrangian. Their intersections display rigidity properties not possessed by smooth manifolds; the Arnold conjecture gives the sum of the submanifold's Betti numbers as a lower bound for the number of self intersections of a smooth Lagrangian submanifold, rather than the Euler characteristic in the smooth case.
Lagrangian submanifolds arise naturally in many physical and geometric situations. We shall see below that caustics
Caustic (optics)
In optics, a caustic or caustic network is the envelope of light rays reflected or refracted by a curved surface or object, or the projection of that envelope of rays on another surface. The caustic is a curve or surface to which each of the light rays is tangent, defining a boundary of an...
can be explained in terms of Lagrangian submanifolds.
Lagrangian fibration
A Lagrangian fibration of a symplectic manifold M is a fibrationFibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
where all of the fibres are Lagrangian submanifolds. Since M is even dimensional we can take local coordinates and by Darboux's theorem
Darboux's theorem
Darboux's theorem is a theorem in the mathematical field of differential geometry and more specifically differential forms, partially generalizing the Frobenius integration theorem. It is a foundational result in several fields, the chief among them being symplectic geometry...
the symplectic form ω can be, at least locally, written as , where d denotes the exterior derivative
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
and ∧ denotes the exterior product. Using this set-up we can locally think of M as being the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
T*Rn, and the Lagrangian fibration as the trivial fibration This is the canonical picture.
Lagrangian mapping
Let L be a Lagrangian submanifold of a symplectic manifold (K,ω) given by an immersion (i is called a Lagrangian immersion). Let give a Lagrangian fibration of K. The composite is a Lagrangian mapping. The critical value setCritical value
-Differential topology:In differential topology, a critical value of a differentiable function between differentiable manifolds is the image ƒ in N of a critical point x in M.The basic result on critical values is Sard's lemma...
of π ○ i is called a caustic
Caustic (mathematics)
In differential geometry and geometric optics, a caustic is the envelope of rays either reflected or refracted by a manifold. It is related to the optical concept of caustics...
.
Two Lagrangian maps and are called Lagrangian equivalent if there exist diffeomorphisms σ, τ and ν such that both sides of the diagram given on the right commute, and τ preserves the symplectic form. Symbolically:
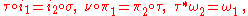
where τ*ω2 denotes the pull back of ω2 by τ.
Special cases and generalizations
- A symplectic manifold endowed with a metricMetric tensorIn the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
that is compatible with the symplectic form is an almost Kähler manifold in the sense that the tangent bundle has an almost complex structure, but this need not be integrable. Symplectic manifolds are special cases of a Poisson manifoldPoisson manifoldIn mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
. The definition of a symplectic manifold requires that the symplectic form be non-degenerate everywhere, but if this condition is violated, the manifold may still be a Poisson manifold.
- A multisymplectic manifold of degree k is a manifold equipped with a closed nondegenerate k-form. See F. Cantrijn, L. A. Ibort and M. de León, J. Austral. Math. Soc. Ser. A 66 (1999), no. 3, 303-330.
- A polysymplectic manifold is a Legendre bundle provided with a polysymplectic tangent-valued
 -form; it is utilized in Hamiltonian field theory. See: G. Giachetta, L. Mangiarotti and G. Sardanashvily, Covariant Hamiltonian equations for field theory, Journal of Physics A32 (1999) 6629-6642; arXiv: hep-th/9904062.
-form; it is utilized in Hamiltonian field theory. See: G. Giachetta, L. Mangiarotti and G. Sardanashvily, Covariant Hamiltonian equations for field theory, Journal of Physics A32 (1999) 6629-6642; arXiv: hep-th/9904062.
External links
- Sardanashvily, G.Gennadi SardanashvilyGennadi Sardanashvily is a theoretical physicist, a principal research scientist of Moscow State University.- Biography :...
, Fibre bundles, jet manifolds and Lagrangian theory. Lectures for theoreticians,arXiv: 0908.1886

