
Gennadi Sardanashvily
Encyclopedia
Gennadi Sardanashvily (born March 13, 1950, Moscow
) is a theoretical physicist, a principal research scientist of Moscow State University
.
(MSU) in 1973, he was a Ph.D. student of the Department of Theoretical Physics (MSU
) in 1973–76, where he held a position in 1976.
He attained his Ph.D. degree in physics and mathematics from MSU
, in 1980, with Dmitri Ivanenko
as his supervisor, and his D.Sc. degree in physics and mathematics from MSU
, in 1998.
Gennadi Sardanashvily is the Managing Editor of the International Journal of Geometric Methods in Modern Physics
(IJGMMP).
and quantum mechanics
and field theory
, gravitation theory
. His main achievement is geometric formulation of classical field theory
and non-autonomous mechanics
including:
Gennadi Sardanashvily has published more than 300 scientific works, including 20 books.
Moscow
Moscow is the capital, the most populous city, and the most populous federal subject of Russia. The city is a major political, economic, cultural, scientific, religious, financial, educational, and transportation centre of Russia and the continent...
) is a theoretical physicist, a principal research scientist of Moscow State University
Moscow State University
Lomonosov Moscow State University , previously known as Lomonosov University or MSU , is the largest university in Russia. Founded in 1755, it also claims to be one of the oldest university in Russia and to have the tallest educational building in the world. Its current rector is Viktor Sadovnichiy...
.
Biography
Gennadi Sardanashvily graduated from Moscow State UniversityMoscow State University
Lomonosov Moscow State University , previously known as Lomonosov University or MSU , is the largest university in Russia. Founded in 1755, it also claims to be one of the oldest university in Russia and to have the tallest educational building in the world. Its current rector is Viktor Sadovnichiy...
(MSU) in 1973, he was a Ph.D. student of the Department of Theoretical Physics (MSU
Moscow State University
Lomonosov Moscow State University , previously known as Lomonosov University or MSU , is the largest university in Russia. Founded in 1755, it also claims to be one of the oldest university in Russia and to have the tallest educational building in the world. Its current rector is Viktor Sadovnichiy...
) in 1973–76, where he held a position in 1976.
He attained his Ph.D. degree in physics and mathematics from MSU
Moscow State University
Lomonosov Moscow State University , previously known as Lomonosov University or MSU , is the largest university in Russia. Founded in 1755, it also claims to be one of the oldest university in Russia and to have the tallest educational building in the world. Its current rector is Viktor Sadovnichiy...
, in 1980, with Dmitri Ivanenko
Dmitri Ivanenko
Dmitri Ivanenko , Professor of Moscow State University , made a great contribution to the physical science of the twentieth century, especially to nuclear physics, field theory , and gravitation theory.His outstanding achievements include:* the Fock-Ivanenko coefficients of parallel...
as his supervisor, and his D.Sc. degree in physics and mathematics from MSU
Moscow State University
Lomonosov Moscow State University , previously known as Lomonosov University or MSU , is the largest university in Russia. Founded in 1755, it also claims to be one of the oldest university in Russia and to have the tallest educational building in the world. Its current rector is Viktor Sadovnichiy...
, in 1998.
Gennadi Sardanashvily is the Managing Editor of the International Journal of Geometric Methods in Modern Physics
International Journal of Geometric Methods in Modern Physics
The International Journal of Geometric Methods in Modern Physics is a peer-reviewed journal, published by World Scientific, covering mathematical physics. It was originally published bimonthly beginning in January 2004; as of 2006 it appears 8 times a year...
(IJGMMP).
Research area
Gennadi Sardanashvily research area is geometric methods in classicalClassical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
and quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
and field theory
Classical field theory
A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
, gravitation theory
Gravitation
Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
. His main achievement is geometric formulation of classical field theory
Classical field theory
A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
and non-autonomous mechanics
Non-autonomous mechanics
Non-autonomous mechanics describe non-relativistic mechanical systems subject to time-dependent transformations. In particular, this is the case of mechanical systems whose Lagrangians and Hamiltonians depend on the time. The configuration space of non-autonomous mechanics isa fiber bundle Q\to...
including:
- gauge gravitation theoryGauge gravitation theoryIn quantum field theory, gauge gravitation theory is the effort to extend Yang–Mills theory, which provides a universal description of the fundamental interactions, to describe gravity.The first gauge model of gravity was...
, where gravity is treated as a Higgs field associated to a reduced Lorentz structure on a world manifold
- geometric formulation of classical field theoryClassical field theoryA classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
and Lagrangian BRST theory where classical fields are represented by sections of fiber bundleFiber bundleIn mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
s and their dynamics is described in terms of jet manifoldsJet bundleIn differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...
and the variational bicomplexVariational bicomplexIn mathematics, the Lagrangian theory on fiber bundles is globally formulated in algebraic terms of the variational bicomplex, without appealing to the calculus of variations...
(covariant classical field theoryCovariant classical field theoryIn recent years, there has been renewed interest in covariant classical field theory. Here, classical fields are represented by sections of fiber bundles and their dynamics is phrased in the context of a finite-dimensional space of fields. Nowadays, it is well known that jet bundles and the...
)
- covariant (polysymplectic) Hamiltonian field theoryCovariant Hamiltonian field theoryApplied to classical field theory, the familiar symplectic Hamiltonian formalism takes the form of instantaneous Hamiltonian formalism on an infinite-dimensional phase space, where canonical coordinates are field functions at some instant of time...
, where momenta correspond to derivatives of fields with respect to all world coordinates
- the second Noether theoremNoether's second theoremIn mathematics, Noether's second theorem relates symmetries of an action functional with a system of differential equations. The action S of a physical system is an integral of a so-called Lagrangian function L, from which the system's behavior can be determined by the principle of least...
in a very general setting of reducible degenerateNoether identitiesIn mathematics, Noether identities characterize the degeneracy of a Lagrangian system. Given a Lagrangian system and its Lagrangian L, Noether identities can be defined as a differential operator whose kernel contains a range of the Euler–Lagrange operator of L...
Grassmann-graded Lagrangian systems on an arbitrary manifold - geometric formulation of classical and quantum non-autonomous mechanicsNon-autonomous mechanicsNon-autonomous mechanics describe non-relativistic mechanical systems subject to time-dependent transformations. In particular, this is the case of mechanical systems whose Lagrangians and Hamiltonians depend on the time. The configuration space of non-autonomous mechanics isa fiber bundle Q\to...
on fiber bundleFiber bundleIn mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
s over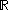
- generalization of the Liouville–Arnold, Nekhoroshev and Mishchenko–Fomenko theorems on completelyIntegrable systemIn mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
and partially integrableIntegrable systemIn mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
and superintegrable Hamiltonian systemSuperintegrable Hamiltonian systemIn mathematics, a superintegrable Hamiltonian system is a Hamiltonian system on a 2n-dimensional symplectic manifold for which the following conditions hold: There exist n ≤ k independent integrals F i of motion...
s to the case of non-compact invariant submanifolds
- cohomology of the variational bicomplexVariational bicomplexIn mathematics, the Lagrangian theory on fiber bundles is globally formulated in algebraic terms of the variational bicomplex, without appealing to the calculus of variations...
of graded differential forms of finite jet order on an infinite order jet manifold.
Gennadi Sardanashvily has published more than 300 scientific works, including 20 books.

