Covariant Hamiltonian field theory
Encyclopedia
Applied to classical field theory
, the familiar symplectic Hamiltonian formalism
takes the form of instantaneous Hamiltonian formalism on an infinite-dimensional phase space, where canonical coordinates are field functions at some instant of time. This Hamiltonian formalism is applied to quantization of fields, e.g., in quantum gauge theory
.
The true Hamiltonian counterpart of classical first order Lagrangian field theory
is covariant Hamiltonian formalism where canonical momenta
correspond to derivatives of fields with respect to all world coordinates 
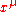. Covariant Hamilton equations are equivalent to the Euler-Lagrange equations in the case of hyperregular Lagrangians. Covariant Hamiltonian field theory is developed in the Hamilton-De Donder, polysymplectic, multisymplectic and 
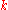-symplectic variants. A phase space of covariant Hamiltonian field theory is a finite-dimensional polysymplectic
or multisymplectic
manifold.
Hamiltonian non-autonomous mechanics
is formulated as covariant Hamiltonian field theory on fiber bundles over the time axis
.
Classical field theory
A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
, the familiar symplectic Hamiltonian formalism
Hamiltonian system
In physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....
takes the form of instantaneous Hamiltonian formalism on an infinite-dimensional phase space, where canonical coordinates are field functions at some instant of time. This Hamiltonian formalism is applied to quantization of fields, e.g., in quantum gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
.
The true Hamiltonian counterpart of classical first order Lagrangian field theory
Classical field theory
A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
is covariant Hamiltonian formalism where canonical momenta
correspond to derivatives of fields with respect to all world coordinates 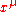. Covariant Hamilton equations are equivalent to the Euler-Lagrange equations in the case of hyperregular Lagrangians. Covariant Hamiltonian field theory is developed in the Hamilton-De Donder, polysymplectic, multisymplectic and 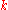-symplectic variants. A phase space of covariant Hamiltonian field theory is a finite-dimensional polysymplecticSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
or multisymplectic
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
manifold.
Hamiltonian non-autonomous mechanics
Non-autonomous mechanics
Non-autonomous mechanics describe non-relativistic mechanical systems subject to time-dependent transformations. In particular, this is the case of mechanical systems whose Lagrangians and Hamiltonians depend on the time. The configuration space of non-autonomous mechanics isa fiber bundle Q\to...
is formulated as covariant Hamiltonian field theory on fiber bundles over the time axis
.See also
- Covariant classical field theoryCovariant classical field theoryIn recent years, there has been renewed interest in covariant classical field theory. Here, classical fields are represented by sections of fiber bundles and their dynamics is phrased in the context of a finite-dimensional space of fields. Nowadays, it is well known that jet bundles and the...
- Symplectic manifoldSymplectic manifoldIn mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
- Non-autonomous mechanicsNon-autonomous mechanicsNon-autonomous mechanics describe non-relativistic mechanical systems subject to time-dependent transformations. In particular, this is the case of mechanical systems whose Lagrangians and Hamiltonians depend on the time. The configuration space of non-autonomous mechanics isa fiber bundle Q\to...