
Non-autonomous mechanics
Encyclopedia
Non-autonomous mechanics describe non-relativistic mechanical systems subject to time-dependent transformations. In particular, this is the case of mechanical systems whose Lagrangian
s and Hamiltonian
s depend on the time. The configuration space of non-autonomous mechanics is
a fiber bundle
 over the time axis
over the time axis  coordinated by
coordinated by 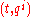 . This bundle is trivial, but its different trivializations
. This bundle is trivial, but its different trivializations  correspond to the choice of different non-relativistic reference frames.
correspond to the choice of different non-relativistic reference frames.
As a consequence, non-autonomous mechanics (in particular, non-autonomous Hamiltonian mechanics) can be formulated as a covariant classical field theory
(in particular covariant Hamiltonian field theory
) on . Accordingly, the velocity phase space of non-autonomous mechanics is the jet manifold
. Accordingly, the velocity phase space of non-autonomous mechanics is the jet manifold
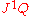 of
of
 provided with the coordinates
provided with the coordinates 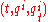 . Its momentum phase space is the vertical cotangent bundle
. Its momentum phase space is the vertical cotangent bundle  of
of  coordinated by
coordinated by 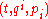 and endowed with the canonical Poisson structure
and endowed with the canonical Poisson structure
. The dynamics of Hamiltonian non-autonomous mechanics is defined by a Hamiltonian form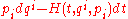 .
.
One can associate to any Hamiltonian non-autonomous system an equivalent Hamiltonian autonomous system on the cotangent bundle of
of  coordinated by
coordinated by 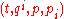 and provided with the canonical symplectic form
and provided with the canonical symplectic form
; its Hamiltonian
is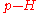 .
.
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
s and Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
s depend on the time. The configuration space of non-autonomous mechanics is
a fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
 over the time axis
over the time axis  coordinated by
coordinated by 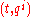 . This bundle is trivial, but its different trivializations
. This bundle is trivial, but its different trivializations  correspond to the choice of different non-relativistic reference frames.
correspond to the choice of different non-relativistic reference frames.As a consequence, non-autonomous mechanics (in particular, non-autonomous Hamiltonian mechanics) can be formulated as a covariant classical field theory
Covariant classical field theory
In recent years, there has been renewed interest in covariant classical field theory. Here, classical fields are represented by sections of fiber bundles and their dynamics is phrased in the context of a finite-dimensional space of fields. Nowadays, it is well known that jet bundles and the...
(in particular covariant Hamiltonian field theory
Covariant Hamiltonian field theory
Applied to classical field theory, the familiar symplectic Hamiltonian formalism takes the form of instantaneous Hamiltonian formalism on an infinite-dimensional phase space, where canonical coordinates are field functions at some instant of time...
) on
 . Accordingly, the velocity phase space of non-autonomous mechanics is the jet manifold
. Accordingly, the velocity phase space of non-autonomous mechanics is the jet manifoldJet bundle
In differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...
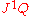 of
of provided with the coordinates
provided with the coordinates 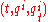 . Its momentum phase space is the vertical cotangent bundle
. Its momentum phase space is the vertical cotangent bundle  of
of  coordinated by
coordinated by 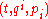 and endowed with the canonical Poisson structure
and endowed with the canonical Poisson structurePoisson manifold
In mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
. The dynamics of Hamiltonian non-autonomous mechanics is defined by a Hamiltonian form
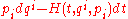 .
.One can associate to any Hamiltonian non-autonomous system an equivalent Hamiltonian autonomous system on the cotangent bundle
 of
of  coordinated by
coordinated by 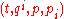 and provided with the canonical symplectic form
and provided with the canonical symplectic formSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
; its Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
is
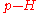 .
.See also
- Analytical mechanicsAnalytical mechanicsAnalytical mechanics is a term used for a refined, mathematical form of classical mechanics, constructed from the 18th century onwards as a formulation of the subject as founded by Isaac Newton. Often the term vectorial mechanics is applied to the form based on Newton's work, to contrast it with...
- Hamiltonian mechanicsHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
- Symplectic manifoldSymplectic manifoldIn mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
- Covariant Hamiltonian field theoryCovariant Hamiltonian field theoryApplied to classical field theory, the familiar symplectic Hamiltonian formalism takes the form of instantaneous Hamiltonian formalism on an infinite-dimensional phase space, where canonical coordinates are field functions at some instant of time...

