Gauge theory
Encyclopedia
In physics
, gauge invariance (also called gauge symmetry) is the property of a field theory
in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory. A transformation from one such field configuration to another is called a gauge transformation.
Modern physical theories describe reality in terms of fields
, e.g., the electromagnetic field
, the gravitational field
, and fields for the electron and all other elementary particles. A general feature of these theories is that none of these fundamental fields, which are the fields that change under a gauge transformation, can be directly measured. On the other hand, the observable quantities, namely the ones that can be measured experimentally — charges, energies, velocities, etc. — do not change under a gauge transformation, even though they are derived from the fields that do change. This (and any) kind of invariance under a transformation is called a symmetry
.
For example, in classical electromagnetism
the electric field
, E, and the magnetic field
, B, are observable, while the underlying and more fundamental electromagnetic potentials V and A are not. Under a gauge transformation which jointly alters the two potentials, no change occurs either in E or B or in the motion of charged particles. In this example, the gauge transformation was just a mathematical feature without any physical significance, except that gauge invariance is intrinsically connected to the fundamental law of charge conservation
.
With the advent of quantum mechanics
in the 1920s, and with successive advances in quantum field theory
, the importance of gauge transformations has steadily grown. Gauge theories constrain the laws of physics, because all the changes induced by a gauge transformation have to cancel each other out when written in terms of observable quantities. Over the course of the 20th century, physicists gradually realized that all forces (fundamental interaction
s) arise from the constraints imposed by local gauge symmetries
, in which case the transformations vary from point to point in space and time
. Perturbative
quantum field theory
(usually employed for scattering theory) describes forces in terms of force mediating particles called gauge boson
s. The nature of these particles is determined by the nature of the gauge transformations. The culmination of these efforts is the Standard Model
, a quantum field theory explaining all of the fundamental interactions except gravity.
's formulation of electrodynamics in 1864. The importance of this symmetry remained unnoticed in the earliest formulations. Similarly unnoticed, Hilbert
had derived Einstein's equations of general relativity by postulating a symmetry under any change of coordinates. Later Hermann Weyl
, in an attempt to unify general relativity
and electromagnetism
, conjectured (incorrectly, as it turned out) that invariance under the change of scale (or "gauge") might also be a local symmetry of general relativity. Although Weyl's choice of the gauge was incorrect, the name "gauge" stuck to the approach. After the development of quantum mechanics
, Weyl, Fock
and London
modified their gauge choice by replacing the scale factor with a change of wave phase
, and applying it successfully to electromagnetism. Gauge symmetry was generalized mathematically in 1954 by Chen Ning Yang and Robert Mills
in an attempt to describe the strong nuclear forces. This idea, dubbed Yang-Mills, later found application in the quantum field theory
of the weak force, and its unification with electromagnetism in the electroweak theory.
The importance of gauge theories for physics stems from their tremendous success in providing a unified framework to describe the quantum-mechanical behavior
of electromagnetism
, the weak force and the strong force. This gauge theory, known as the Standard Model
, accurately describes experimental predictions regarding three of the four fundamental forces of nature.
. A static electric field can be described in terms of an electric potential
(voltage) that is defined at every point in space, and in practical work it is conventional to take the Earth as a physical reference that defines the zero level of the potential, or ground. But only differences in potential are physically measurable, which is the reason that a voltmeter
must have two probes, and can only report the voltage difference between them. Thus one could choose to define all voltage differences relative to some other standard, rather than the Earth, resulting in the addition of a constant offset. If the potential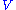
is a solution to Maxwell's equations
then, after this gauge transformation, the new potential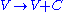
is also a solution to Maxwell's equations and no experiment can distinguish between these two solutions. In other words the laws of physics governing electricity and magnetism (that is, Maxwell equations) are invariant under gauge transformation. That is, Maxwell's equations have a gauge symmetry.
Generalizing from static electricity to electromagnetism, we have a second potential, the magnetic vector potential A, which can also undergo gauge transformations. These transformations may also be local. That is, rather than adding a constant onto V, one can add a function that takes on different values at different points in space and time. If A is also changed in certain corresponding ways, then the same E and B fields result. The detailed mathematical relationship between the fields E and B and the potentials V and A is given in the article Gauge fixing
, along with the precise statement of the nature of the gauge transformation. The relevant point here is that the fields remain the same under the gauge transformation, and therefore Maxwell's equations
are still satisfied.
Gauge symmetry is closely related to charge conservation
. Suppose that there existed some process by which one could violate conservation of charge, at least temporarily, by creating a charge q at a certain point in space, 1, moving it to some other point 2, and then destroying it. We might imagine that this process was consistent with conservation of energy. We could posit a rule stating that creating the charge required an input of energy E1=qV1 and destroying it released E2=qV2, which would seem natural since qV measures the extra energy stored in the electric field because of the existence of a charge at a certain point. (There may also be energy associated, e.g., with the rest mass of the particle, but that is not relevant to the present argument.) Conservation of energy would be satisfied, because the net energy released by creation and destruction of the particle, qV2-qV1, would be equal to the work done in moving the particle from 1 to 2, qV2-qV1. But although this scenario salvages conservation of energy, it violates gauge symmetry. Gauge symmetry requires that the laws of physics be invariant under the transformation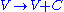
, which implies that no experiment should be able to measure the absolute potential, without reference to some external standard such as an electrical ground. But the proposed rules E1=qV1 and E2=qV2 for the energies of creation and destruction would allow an experimenter to determine the absolute potential, simply by checking how much energy input was required in order to create the charge q at a particular point in space. The conclusion is that if gauge symmetry holds, and energy is conserved, then charge must be conserved.
are arbitrary coordinate transformations. (Technically, the transformations must be invertible, and both the transformation and its inverse must be smooth, in the sense of being differentiable an arbitrary number of times.)
concept that various places in space, such as the earth and the heavens, obeyed different physical rules.
Suppose, for example, that one observer examines the properties of a hydrogen atom on Earth, the other—on the Moon (or any other place in the universe), the observer will find that their hydrogen atoms exhibit completely identical properties. Again, if one observer had examined a hydrogen atom today and the other—100 years ago (or any other time in the past or in the future), the two experiments would again produce completely identical results. The invariance of the properties of a hydrogen atom with respect to the time when, and place where, these properties were investigated is called translation invariance.
Recalling our two observers from different ages: the time in their experiments is shifted by 100 years. If the time when the older observer did the experiment was t, the time of the modern experiment is t+100 years. Both observers discover the same laws of physics. Because light from hydrogen atoms in distant galaxies may reach the earth after having traveled across space for billions of years, in effect one can do such observations covering periods of time almost all the way back to the Big Bang
, and they showed that the laws of physics had always been the same.
In other words, if in the theory we change the time t to t+100 years (or indeed any other time shift) the theoretical predictions do not change.
, coordinates like x, y, z, and t are not only "relative" in the global sense of translations like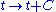
, rotations, etc., but become completely arbitrary, so that for example one can define an entirely new timelike coordinate according to some arbitrary rule such as 
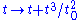, where 
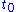has units of time, and yet Einstein's equations will have the same form.
Invariance of the form of an equation under an arbitrary coordinate transformation is customarily referred to as general covariance
and equations with this property are referred to as written in the covariant form. General covariance is a subclass of gauge invariance.
Maxwell's equations can also be expressed in a generally covariant form, which is as invariant under general coordinate transformation as Einstein's field equation.
is performed with electrons, then a wave-like interference pattern is observed. The electron has the highest probability of being detected at locations where the parts of the wave passing through the two slits are in phase with one another, resulting in constructive interference. The frequency of the electron wave is related to the kinetic energy of an individual electron particle via the quantum-mechanical relation E=hf. If there are no electric or magnetic fields present in this experiment, then the electron's energy is constant, and, for example, there will be a high probability of detecting the electron along the central axis of the experiment, where by symmetry the two parts of the wave are in phase.
But now suppose that the electrons in the experiment are subject to electric or magnetic fields. For example, if an electric field was imposed on one side of the axis but not on the other, the results of the experiment would be affected. The part of the electron wave passing through that side oscillates at a different rate, since its energy has had -eV added to it, where -e is the charge of the electron and V the electrical potential. The results of the experiment will be different, because phase relationships between the two parts of the electron wave have changed, and therefore the locations of constructive and destructive interference will be shifted to one side or the other. It is the electric potential that occurs here, not the electric field, and this is a manifestation of the fact that it is the potentials and not the fields that are of fundamental significance in quantum mechanics.
, gauge symmetry applies to both electromagnetic waves and electron waves. These two gauge symmetries are in fact intimately related. If a gauge transformation θ is applied to the electron waves, for example, then one must also apply a corresponding transformation to the potentials that describe the electromagnetic waves. Gauge symmetry is required in order to make quantum electrodynamics a renormalizable
theory, i.e., one in which the calculated predictions of all physically measurable quantities are finite.
In mathematical terminology, electron phases form an Abelian group
under addition, called the circle group or U(1). "Abelian" means that addition commutes, so that θ + φ = φ + θ. Group
means that addition associates
and has an identity element
, namely "0". Also, for every phase there exists an inverse
such that the sum of a phase and its inverse is 0. Other examples of abelian groups are the integers under addition, 0, and negation, and the nonzero fractions under product, 1, and reciprocal.
As a way of visualizing the choice of a gauge, consider whether it is possible to tell if a cylinder has been twisted. If the cylinder has no bumps, marks, or scratches on it, we cannot tell. We could, however, draw an arbitrary curve along the cylinder, defined by some function θ(x), where x measures distance along the axis of the cylinder. Once this arbitrary choice (the choice of gauge) has been made, it becomes possible to detect it if someone later twists the cylinder.
In 1954, Chen Ning Yang and Robert Mills
proposed to generalize these ideas to noncommutative groups. A noncommutative gauge group can describe a field that, unlike the electromagnetic field, interacts with itself. For example, general relativity
states that gravitational fields have energy, and special relativity
concludes that energy is equivalent to mass. Hence a gravitational field induces a further gravitational field. The nuclear forces also have this self-interacting property.
, which allows waves to be added, subtracted, and mixed arbitrarily. It follows that we are not even restricted to a complete swaps of identity. For example, if we observe that a certain amount of energy exists in a certain location in space, there is no experiment that can tell us whether that energy is 100% A's and 0% B's, 0% A's and 100% B's, or 20% A's and 80% B's, or some other mixture. The fact that the symmetry is local means that we cannot even count on these proportions to remain fixed as the particles propagate through space. The details of how this is represented mathematically depend on technical issues relating to the spins
of the particles, but for our present purposes we consider a spinless particle, for which it turns out that the mixing can be specified by some arbitrary choice of gauge θ(x), where an angle θ = 0° represents 100% A and 0% B, θ = 90° means 0% A and 100% B, and intermediate angles represent mixtures.
According to the principles of quantum mechanics, particles do not actually have trajectories through space. Motion can only be described in terms of waves, and the momentum p of an individual particle is related to its wavelength λ by p = h/λ. In terms of empirical measurements, the wavelength can only be determined by observing a change in the wave between one point in space and another nearby point (mathematically, by differentiation
). A wave with a shorter wavelength oscillates more rapidly, and therefore changes more rapidly between nearby points. Now suppose that we arbitrarily fix a gauge at one point in space, by saying that the energy at that location is 20% A's and 80% B's. We then measure the two waves at some other, nearby point, in order to determine their wavelengths. But there are two entirely different reasons that the waves could have changed. They could have changed because they were oscillating with a certain wavelength, or they could have changed because the gauge function changed from a 20-80 mixture to, say, 21-79. If we ignore the second possibility, the resulting theory doesn't work; strange discrepancies in momentum will show up, violating the principle of conservation of momentum. Something in the theory must be changed.
Again there are technical issues relating to spin, but in several important cases, including electrically charged particles and particles interacting via nuclear forces, the solution to the problem is to impute physical reality to the gauge function θ(x). We say that if the function θ oscillates, it represents a new type of quantum-mechanical wave, and this new wave has its own momentum p = h/λ, which turns out to patch up the discrepancies that otherwise would have broken conservation of momentum. In the context of electromagnetism, the particles A and B would be charged particles such as electrons, and the quantum mechanical wave represented by θ would be the electromagnetic field. (Here we ignore the technical issues raised by the fact that electrons actually have spin 1/2, not spin zero. This oversimplification is the reason that the gauge field θ comes out to be a scalar, whereas the electromagnetic field is actually represented by a vector consisting of V and A.) The result is that we have an explanation for the presence of electromagnetic interactions: if we try to construct a gauge-symmetric theory of identical, non-interacting particles, the result is not self-consistent, and can only be repaired by adding electrical and magnetic fields that cause the particles to interact.
Although the function θ(x) describes a wave, the laws of quantum mechanics require that it also have particle properties. In the case of electromagnetism, the particle corresponding to electromagnetic waves is the photon. In general, such particles are called gauge bosons, where the term "boson" refers to a particle with integer spin. In the simplest versions of the theory, gauge bosons are massless, but it is also possible to construct versions in which they have mass, as is the case for the gauge bosons that transmit the nuclear forces.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, gauge invariance (also called gauge symmetry) is the property of a field theory
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory. A transformation from one such field configuration to another is called a gauge transformation.
Modern physical theories describe reality in terms of fields
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
, e.g., the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
, the gravitational field
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
, and fields for the electron and all other elementary particles. A general feature of these theories is that none of these fundamental fields, which are the fields that change under a gauge transformation, can be directly measured. On the other hand, the observable quantities, namely the ones that can be measured experimentally — charges, energies, velocities, etc. — do not change under a gauge transformation, even though they are derived from the fields that do change. This (and any) kind of invariance under a transformation is called a symmetry
Symmetry in physics
In physics, symmetry includes all features of a physical system that exhibit the property of symmetry—that is, under certain transformations, aspects of these systems are "unchanged", according to a particular observation...
.
For example, in classical electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
, E, and the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
, B, are observable, while the underlying and more fundamental electromagnetic potentials V and A are not. Under a gauge transformation which jointly alters the two potentials, no change occurs either in E or B or in the motion of charged particles. In this example, the gauge transformation was just a mathematical feature without any physical significance, except that gauge invariance is intrinsically connected to the fundamental law of charge conservation
Charge conservation
In physics, charge conservation is the principle that electric charge can neither be created nor destroyed. The net quantity of electric charge, the amount of positive charge minus the amount of negative charge in the universe, is always conserved...
.
With the advent of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
in the 1920s, and with successive advances in quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, the importance of gauge transformations has steadily grown. Gauge theories constrain the laws of physics, because all the changes induced by a gauge transformation have to cancel each other out when written in terms of observable quantities. Over the course of the 20th century, physicists gradually realized that all forces (fundamental interaction
Fundamental interaction
In particle physics, fundamental interactions are the ways that elementary particles interact with one another...
s) arise from the constraints imposed by local gauge symmetries
Local symmetry
In physics, a local symmetry is symmetry of some physical quantity, which smoothly depends on the point of the base manifold. Such quantities can be for example an observable, a tensor or the Lagrangian of a theory....
, in which case the transformations vary from point to point in space and time
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. Perturbative
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
(usually employed for scattering theory) describes forces in terms of force mediating particles called gauge boson
Gauge boson
In particle physics, gauge bosons are bosonic particles that act as carriers of the fundamental forces of nature. More specifically, elementary particles whose interactions are described by gauge theory exert forces on each other by the exchange of gauge bosons, usually as virtual particles.-...
s. The nature of these particles is determined by the nature of the gauge transformations. The culmination of these efforts is the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
, a quantum field theory explaining all of the fundamental interactions except gravity.
History and importance
The earliest field theory having a gauge symmetry was MaxwellJames Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
's formulation of electrodynamics in 1864. The importance of this symmetry remained unnoticed in the earliest formulations. Similarly unnoticed, Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
had derived Einstein's equations of general relativity by postulating a symmetry under any change of coordinates. Later Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
, in an attempt to unify general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
and electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, conjectured (incorrectly, as it turned out) that invariance under the change of scale (or "gauge") might also be a local symmetry of general relativity. Although Weyl's choice of the gauge was incorrect, the name "gauge" stuck to the approach. After the development of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, Weyl, Fock
Vladimir Fock
Vladimir Aleksandrovich Fock was a Soviet physicist, who did foundational work on quantum mechanics and quantum electrodynamics....
and London
Fritz London
Fritz Wolfgang London was a German theoretical physicist. His fundamental contributions to the theories of chemical bonding and of intermolecular forces are today considered classic and are discussed in standard textbooks of physical chemistry.With his brother Heinz, he made a significant...
modified their gauge choice by replacing the scale factor with a change of wave phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
, and applying it successfully to electromagnetism. Gauge symmetry was generalized mathematically in 1954 by Chen Ning Yang and Robert Mills
Robert Mills (physicist)
Robert L. Mills was a physicist, specializing in quantum field theory, the theory of alloys, and many-body theory. While sharing an office at Brookhaven National Laboratory, in 1954, Chen Ning Yang and Mills proposed a tensor equation for what are now called Yang-Mills fields...
in an attempt to describe the strong nuclear forces. This idea, dubbed Yang-Mills, later found application in the quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
of the weak force, and its unification with electromagnetism in the electroweak theory.
The importance of gauge theories for physics stems from their tremendous success in providing a unified framework to describe the quantum-mechanical behavior
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
of electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, the weak force and the strong force. This gauge theory, known as the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
, accurately describes experimental predictions regarding three of the four fundamental forces of nature.
Electromagnetism
Historically, the first example of gauge symmetry to be discovered was classical electromagnetismElectromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
. A static electric field can be described in terms of an electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
(voltage) that is defined at every point in space, and in practical work it is conventional to take the Earth as a physical reference that defines the zero level of the potential, or ground. But only differences in potential are physically measurable, which is the reason that a voltmeter
Voltmeter
A voltmeter is an instrument used for measuring electrical potential difference between two points in an electric circuit. Analog voltmeters move a pointer across a scale in proportion to the voltage of the circuit; digital voltmeters give a numerical display of voltage by use of an analog to...
must have two probes, and can only report the voltage difference between them. Thus one could choose to define all voltage differences relative to some other standard, rather than the Earth, resulting in the addition of a constant offset. If the potential
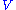is a solution to Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
then, after this gauge transformation, the new potential
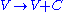is also a solution to Maxwell's equations and no experiment can distinguish between these two solutions. In other words the laws of physics governing electricity and magnetism (that is, Maxwell equations) are invariant under gauge transformation. That is, Maxwell's equations have a gauge symmetry.Generalizing from static electricity to electromagnetism, we have a second potential, the magnetic vector potential A, which can also undergo gauge transformations. These transformations may also be local. That is, rather than adding a constant onto V, one can add a function that takes on different values at different points in space and time. If A is also changed in certain corresponding ways, then the same E and B fields result. The detailed mathematical relationship between the fields E and B and the potentials V and A is given in the article Gauge fixing
Gauge fixing
In the physics of gauge theories, gauge fixing denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field...
, along with the precise statement of the nature of the gauge transformation. The relevant point here is that the fields remain the same under the gauge transformation, and therefore Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
are still satisfied.
Gauge symmetry is closely related to charge conservation
Charge conservation
In physics, charge conservation is the principle that electric charge can neither be created nor destroyed. The net quantity of electric charge, the amount of positive charge minus the amount of negative charge in the universe, is always conserved...
. Suppose that there existed some process by which one could violate conservation of charge, at least temporarily, by creating a charge q at a certain point in space, 1, moving it to some other point 2, and then destroying it. We might imagine that this process was consistent with conservation of energy. We could posit a rule stating that creating the charge required an input of energy E1=qV1 and destroying it released E2=qV2, which would seem natural since qV measures the extra energy stored in the electric field because of the existence of a charge at a certain point. (There may also be energy associated, e.g., with the rest mass of the particle, but that is not relevant to the present argument.) Conservation of energy would be satisfied, because the net energy released by creation and destruction of the particle, qV2-qV1, would be equal to the work done in moving the particle from 1 to 2, qV2-qV1. But although this scenario salvages conservation of energy, it violates gauge symmetry. Gauge symmetry requires that the laws of physics be invariant under the transformation
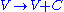, which implies that no experiment should be able to measure the absolute potential, without reference to some external standard such as an electrical ground. But the proposed rules E1=qV1 and E2=qV2 for the energies of creation and destruction would allow an experimenter to determine the absolute potential, simply by checking how much energy input was required in order to create the charge q at a particular point in space. The conclusion is that if gauge symmetry holds, and energy is conserved, then charge must be conserved.General relativity
As discussed above, the gauge transformations for classical (i.e., non-quantum mechanical) general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
are arbitrary coordinate transformations. (Technically, the transformations must be invertible, and both the transformation and its inverse must be smooth, in the sense of being differentiable an arbitrary number of times.)
An example of a symmetry in a physical theory: translation invariance
Some global symmetries under changes of coordinate predate both general relativity and the concept of a gauge. For example, translation invariance was introduced in the era of Galileo, who eliminated the AristotelianAristotelian physics
Aristotelian Physics the natural sciences, are described in the works of the Greek philosopher Aristotle . In the Physics, Aristotle established general principles of change that govern all natural bodies; both living and inanimate, celestial and terrestrial—including all motion, change in respect...
concept that various places in space, such as the earth and the heavens, obeyed different physical rules.
Suppose, for example, that one observer examines the properties of a hydrogen atom on Earth, the other—on the Moon (or any other place in the universe), the observer will find that their hydrogen atoms exhibit completely identical properties. Again, if one observer had examined a hydrogen atom today and the other—100 years ago (or any other time in the past or in the future), the two experiments would again produce completely identical results. The invariance of the properties of a hydrogen atom with respect to the time when, and place where, these properties were investigated is called translation invariance.
Recalling our two observers from different ages: the time in their experiments is shifted by 100 years. If the time when the older observer did the experiment was t, the time of the modern experiment is t+100 years. Both observers discover the same laws of physics. Because light from hydrogen atoms in distant galaxies may reach the earth after having traveled across space for billions of years, in effect one can do such observations covering periods of time almost all the way back to the Big Bang
Big Bang
The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
, and they showed that the laws of physics had always been the same.
In other words, if in the theory we change the time t to t+100 years (or indeed any other time shift) the theoretical predictions do not change.
Another example of a symmetry: the invariance of Einstein's field equation under arbitrary coordinate transformations
In Einstein's general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, coordinates like x, y, z, and t are not only "relative" in the global sense of translations like
, rotations, etc., but become completely arbitrary, so that for example one can define an entirely new timelike coordinate according to some arbitrary rule such as , where 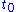has units of time, and yet Einstein's equations will have the same form.Invariance of the form of an equation under an arbitrary coordinate transformation is customarily referred to as general covariance
General covariance
In theoretical physics, general covariance is the invariance of the form of physical laws under arbitrary differentiable coordinate transformations...
and equations with this property are referred to as written in the covariant form. General covariance is a subclass of gauge invariance.
Maxwell's equations can also be expressed in a generally covariant form, which is as invariant under general coordinate transformation as Einstein's field equation.
Quantum electrodynamics
Until the advent of quantum mechanics, the only well known example of gauge symmetry was in electromagnetism, and the general significance of the concept was not fully understood. For example, it was not clear whether it was the fields E and B or the potentials V and A that were the fundamental quantities; if the former, then the gauge transformations could be considered as nothing more than a mathematical trick.Aharonov–Bohm experiment
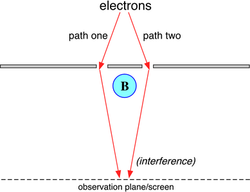
In quantum mechanics, however, a particle such as an electron is also described as a wave. For example, if the double-slit experimentDouble-slit experiment
The double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
is performed with electrons, then a wave-like interference pattern is observed. The electron has the highest probability of being detected at locations where the parts of the wave passing through the two slits are in phase with one another, resulting in constructive interference. The frequency of the electron wave is related to the kinetic energy of an individual electron particle via the quantum-mechanical relation E=hf. If there are no electric or magnetic fields present in this experiment, then the electron's energy is constant, and, for example, there will be a high probability of detecting the electron along the central axis of the experiment, where by symmetry the two parts of the wave are in phase.
But now suppose that the electrons in the experiment are subject to electric or magnetic fields. For example, if an electric field was imposed on one side of the axis but not on the other, the results of the experiment would be affected. The part of the electron wave passing through that side oscillates at a different rate, since its energy has had -eV added to it, where -e is the charge of the electron and V the electrical potential. The results of the experiment will be different, because phase relationships between the two parts of the electron wave have changed, and therefore the locations of constructive and destructive interference will be shifted to one side or the other. It is the electric potential that occurs here, not the electric field, and this is a manifestation of the fact that it is the potentials and not the fields that are of fundamental significance in quantum mechanics.
Explanation with potentials
It is even possible to have cases in which an experiment's results differ when the potentials are changed, even if no charged particle is ever exposed to a different field. One such example is the Aharonov–Bohm effect, shown in the figure. In this example, turning on the solenoid only causes a magnetic field B to exist within the solenoid. But the solenoid has been positioned so that the electron cannot possibly pass through its interior. If one believed that the fields were the fundamental quantities, then one would expect that the results of the experiment would be unchanged. In reality, the results are different, because turning on the solenoid changed the vector potential A in the region that the electrons do pass through. Now that it has been established that it is the potentials V and A that are fundamental, and not the fields E and B, we can see that the gauge transformations, which change V and A have real physical significance, rather than being merely mathematical artifacts.Gauge invariance: the results of the experiments are independent on the choice of the gauge for the potentials
Note that in these experiments, the only quantity that affects the result is the difference in phase between the two parts of the electron wave. Suppose we imagine the two parts of the electron wave as tiny clocks, each with a single hand that sweeps around in a circle, keeping track of its own phase. Although this cartoon ignores some technical details, it retains the physical phenomena that are important here. If both clocks are sped up by the same amount, the phase relationship between them is unchanged, and the results of experiments are the same. Not only that, but it is not even necessary to change the speed of each clock by a fixed amount. We could change the angle of the hand on each clock by a varying amount θ, where θ could depend on both the position in space and on time. This would have no effect on the result of the experiment, since the final observation of the location of the electron occurs at a single place and time, so that the phase shift in each electron's "clock" would be the same, and the two effects would cancel out. This is another example of a gauge transformation: it is local, and it does not change the results of experiments.Summary
In summary, gauge symmetry attains its full importance in the context of quantum mechanics. In the application of quantum mechanics to electromagnetism, i.e., quantum electrodynamicsQuantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
, gauge symmetry applies to both electromagnetic waves and electron waves. These two gauge symmetries are in fact intimately related. If a gauge transformation θ is applied to the electron waves, for example, then one must also apply a corresponding transformation to the potentials that describe the electromagnetic waves. Gauge symmetry is required in order to make quantum electrodynamics a renormalizable
Renormalization
In quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, renormalization is any of a collection of techniques used to treat infinities arising in calculated quantities....
theory, i.e., one in which the calculated predictions of all physically measurable quantities are finite.
Types of gauge symmetries
The description of the electrons in the subsection above as little clocks is in effect a statement of the mathematical rules according to which the phases of electrons are to be added and subtracted: they are to be treated as ordinary numbers, except that in the case where the result of the calculation falls outside the range of 0≤θ<360°, we force it to "wrap around" into the allowed range, which covers a circle. Another way of putting this is that a phase angle of, say, 5° is considered to be completely equivalent to an angle of 365°. Experiments have verified this testable statement about the interference patterns formed by electron waves. Except for the "wrap-around" property, the algebraic properties of this mathematical structure are exactly the same as those of the ordinary real numbers.In mathematical terminology, electron phases form an Abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
under addition, called the circle group or U(1). "Abelian" means that addition commutes, so that θ + φ = φ + θ. Group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
means that addition associates
Associativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
and has an identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
, namely "0". Also, for every phase there exists an inverse
Inverse element
In abstract algebra, the idea of an inverse element generalises the concept of a negation, in relation to addition, and a reciprocal, in relation to multiplication. The intuition is of an element that can 'undo' the effect of combination with another given element...
such that the sum of a phase and its inverse is 0. Other examples of abelian groups are the integers under addition, 0, and negation, and the nonzero fractions under product, 1, and reciprocal.
As a way of visualizing the choice of a gauge, consider whether it is possible to tell if a cylinder has been twisted. If the cylinder has no bumps, marks, or scratches on it, we cannot tell. We could, however, draw an arbitrary curve along the cylinder, defined by some function θ(x), where x measures distance along the axis of the cylinder. Once this arbitrary choice (the choice of gauge) has been made, it becomes possible to detect it if someone later twists the cylinder.
In 1954, Chen Ning Yang and Robert Mills
Robert Mills (physicist)
Robert L. Mills was a physicist, specializing in quantum field theory, the theory of alloys, and many-body theory. While sharing an office at Brookhaven National Laboratory, in 1954, Chen Ning Yang and Mills proposed a tensor equation for what are now called Yang-Mills fields...
proposed to generalize these ideas to noncommutative groups. A noncommutative gauge group can describe a field that, unlike the electromagnetic field, interacts with itself. For example, general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
states that gravitational fields have energy, and special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
concludes that energy is equivalent to mass. Hence a gravitational field induces a further gravitational field. The nuclear forces also have this self-interacting property.
Gauge bosons
Surprisingly, gauge symmetry can give a deeper explanation for the existence of interactions, such as the electrical and nuclear interactions. This arises from a type of gauge symmetry relating to the fact that all particles of a given type are experimentally indistinguishable from one other. Imagine that Alice and Betty are identical twins, labeled at birth by bracelets reading A and B. Because the girls are identical, nobody would be able to tell if they had been switched at birth; the labels A and B are arbitrary, and can be interchanged. Such a permanent interchanging of their identities is like a global gauge symmetry. There is also a corresponding local gauge symmetry, which describes the fact that from one moment to the next, Alice and Betty could swap roles while nobody was looking, and nobody would be able to tell. If we observe that Mom's favorite vase is broken, we can only infer that the blame belongs to one twin or the other, but we cannot tell whether the blame is 100% Alice's and 0% Betty's, or vice versa. If Alice and Betty are in fact quantum-mechanical particles rather than people, then they also have wave properties, including the property of superpositionSuperposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
, which allows waves to be added, subtracted, and mixed arbitrarily. It follows that we are not even restricted to a complete swaps of identity. For example, if we observe that a certain amount of energy exists in a certain location in space, there is no experiment that can tell us whether that energy is 100% A's and 0% B's, 0% A's and 100% B's, or 20% A's and 80% B's, or some other mixture. The fact that the symmetry is local means that we cannot even count on these proportions to remain fixed as the particles propagate through space. The details of how this is represented mathematically depend on technical issues relating to the spins
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
of the particles, but for our present purposes we consider a spinless particle, for which it turns out that the mixing can be specified by some arbitrary choice of gauge θ(x), where an angle θ = 0° represents 100% A and 0% B, θ = 90° means 0% A and 100% B, and intermediate angles represent mixtures.
According to the principles of quantum mechanics, particles do not actually have trajectories through space. Motion can only be described in terms of waves, and the momentum p of an individual particle is related to its wavelength λ by p = h/λ. In terms of empirical measurements, the wavelength can only be determined by observing a change in the wave between one point in space and another nearby point (mathematically, by differentiation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
). A wave with a shorter wavelength oscillates more rapidly, and therefore changes more rapidly between nearby points. Now suppose that we arbitrarily fix a gauge at one point in space, by saying that the energy at that location is 20% A's and 80% B's. We then measure the two waves at some other, nearby point, in order to determine their wavelengths. But there are two entirely different reasons that the waves could have changed. They could have changed because they were oscillating with a certain wavelength, or they could have changed because the gauge function changed from a 20-80 mixture to, say, 21-79. If we ignore the second possibility, the resulting theory doesn't work; strange discrepancies in momentum will show up, violating the principle of conservation of momentum. Something in the theory must be changed.
Again there are technical issues relating to spin, but in several important cases, including electrically charged particles and particles interacting via nuclear forces, the solution to the problem is to impute physical reality to the gauge function θ(x). We say that if the function θ oscillates, it represents a new type of quantum-mechanical wave, and this new wave has its own momentum p = h/λ, which turns out to patch up the discrepancies that otherwise would have broken conservation of momentum. In the context of electromagnetism, the particles A and B would be charged particles such as electrons, and the quantum mechanical wave represented by θ would be the electromagnetic field. (Here we ignore the technical issues raised by the fact that electrons actually have spin 1/2, not spin zero. This oversimplification is the reason that the gauge field θ comes out to be a scalar, whereas the electromagnetic field is actually represented by a vector consisting of V and A.) The result is that we have an explanation for the presence of electromagnetic interactions: if we try to construct a gauge-symmetric theory of identical, non-interacting particles, the result is not self-consistent, and can only be repaired by adding electrical and magnetic fields that cause the particles to interact.
Although the function θ(x) describes a wave, the laws of quantum mechanics require that it also have particle properties. In the case of electromagnetism, the particle corresponding to electromagnetic waves is the photon. In general, such particles are called gauge bosons, where the term "boson" refers to a particle with integer spin. In the simplest versions of the theory, gauge bosons are massless, but it is also possible to construct versions in which they have mass, as is the case for the gauge bosons that transmit the nuclear forces.
Further reading
These books are intended for general readers and employ the barest minimum of mathematics.- Schumm, Bruce (2004) Deep Down Things. Johns Hopkins University Press. A serious attempt by a physicist to explain gauge theory and the Standard Model.
- Feynman, RichardRichard FeynmanRichard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
(2006) QED: The Strange Theory of Light and Matter. Princeton University Press. A nontechnical description of quantum field theory (not specifically about gauge theory).