Superintegrable Hamiltonian system
Encyclopedia
In mathematics, a superintegrable Hamiltonian system is a Hamiltonian system
on a 2n-dimensional symplectic manifold
for which the following conditions hold:
(i) There exist n ≤ k independent integrals F i of motion. Their level surfaces (invariant submanifolds) form a fibered manifold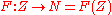
over a connected open subset 
.
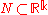(ii) There exist smooth real functions
on 
such that the Poisson bracket
of integrals of motion reads
.
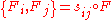(iii) The matrix function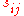
is of constant corank 
on 
.
If
, this is the case of a completely integrable Hamiltonian system
. The Mishchenko-Fomenko theorem for superintegrable Hamiltonian systems generalizes the Liouville-Arnold theorem on action-angle coordinates
of completely integrable Hamiltonian system as follows.
Let invariant submanifolds of a superintegrable Hamiltonian system be connected compact and mutually diffeomorphic. Then the fibered manifold
is a fiber bundle
in tori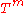
. Given its fiber 
, there exists an open neighbourhood 
of 
which is a trivial fiber bundle provided with the bundle (generalized action-angle) coordinates 
,
, 
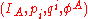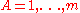such that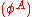 
are coordinates on 
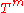. These coordinates are the Darboux coordinates
on a symplectic manifold
. A Hamiltonian of a superintegrable system depends only on the action variables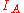 
which are the Casimir functions of the coinduced Poisson structure
on
.
The Liouville-Arnold theorem for completely integrable systems
and the Mishchenko-Fomenko theorem for the superintegrable ones are generalized to the case of non-compact invariant submanifolds. They are diffeomorphic to a toroidal cylinder
.
Hamiltonian system
In physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....
on a 2n-dimensional symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
for which the following conditions hold:
(i) There exist n ≤ k independent integrals F i of motion. Their level surfaces (invariant submanifolds) form a fibered manifold
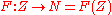over a connected open subset 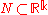.(ii) There exist smooth real functions
on such that the Poisson bracketPoisson manifold
In mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
of integrals of motion reads
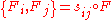.(iii) The matrix function
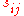is of constant corank on .If
, this is the case of a completely integrable Hamiltonian systemIntegrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
. The Mishchenko-Fomenko theorem for superintegrable Hamiltonian systems generalizes the Liouville-Arnold theorem on action-angle coordinates
Action-angle coordinates
In classical mechanics, action-angle coordinates are a set of canonical coordinates useful in solving many integrable systems. The method of action-angles is useful for obtaining the frequencies of oscillatory or rotational motion without solving the equations of motion. Action-angle coordinates...
of completely integrable Hamiltonian system as follows.
Let invariant submanifolds of a superintegrable Hamiltonian system be connected compact and mutually diffeomorphic. Then the fibered manifold
is a fiber bundleFiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
in tori
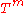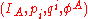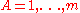. Given its fiber , there exists an open neighbourhood of which is a trivial fiber bundle provided with the bundle (generalized action-angle) coordinates ,, such that 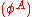are coordinates on 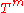. These coordinates are the Darboux coordinatesDarboux's theorem
Darboux's theorem is a theorem in the mathematical field of differential geometry and more specifically differential forms, partially generalizing the Frobenius integration theorem. It is a foundational result in several fields, the chief among them being symplectic geometry...
on a symplectic manifold
. A Hamiltonian of a superintegrable system depends only on the action variables 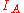which are the Casimir functions of the coinduced Poisson structurePoisson manifold
In mathematics, a Poisson manifold is a differentiable manifold M such that the algebra C^\infty\, of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra...
on
.The Liouville-Arnold theorem for completely integrable systems
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
and the Mishchenko-Fomenko theorem for the superintegrable ones are generalized to the case of non-compact invariant submanifolds. They are diffeomorphic to a toroidal cylinder
.