Action-angle coordinates
Encyclopedia
In classical mechanics
, action-angle coordinates are a set of canonical coordinates
useful in solving many integrable system
s. The method of action-angles is useful for obtaining the frequencies
of oscillatory or rotational motion without solving the equations of motion. Action-angle coordinates are chiefly used when the Hamilton–Jacobi equation
s are completely separable. (Hence, the Hamiltonian
does not depend explicitly on time, i.e., the energy is conserved
.) Action-angle variables define an invariant torus, so called because holding the action constant defines the surface of a torus
, while the angle variables provide the coordinates on the torus.
The Bohr–Sommerfeld quantization conditions, used to develop quantum mechanics before the advent of wave mechanics, state that the action must be an integral multiple of Planck's constant; similarly, Einstein
's insight into EBK quantization and the difficulty of quantizing non-integrable systems was expressed in terms of the invariant tori of action-angle coordinates.
Action-angle coordinates are also useful in perturbation theory
of Hamiltonian mechanics
, especially in determining adiabatic invariant
s. One of the earliest results from chaos theory
, for the non-linear perturbations of dynamical systems with a small number of degrees of freedom is the KAM theorem, which states that the invariant tori are stable under small perturbations.
The use of action-angle variables was central to the solution of the Toda lattice, and to the definition of Lax pairs, or more generally, the idea of the isospectral
evolution of a system.
where the generating function is Hamilton's characteristic function
(not Hamilton's principal function 
). Since the original Hamiltonian does not depend on time explicitly, the new Hamiltonian 
is merely the old Hamiltonian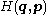 
expressed in terms of the new canonical coordinates
, which we denote as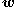
(the action angles, which are the generalized coordinates
) and their new generalized momenta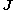
. We will not need to solve here for the generating function 
itself; instead, we will use it merely as a vehicle for relating the new and old canonical coordinates
.
Rather than defining the action angles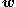
directly, we define instead their generalized momenta, which resemble the classical action
for each original generalized coordinate
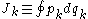
where the integration path is implicitly given by the constant energy function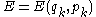
. Since the actual motion is not involved in this integration, these generalized momenta 
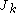are constants of the motion, implying that the transformed Hamiltonian 
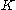does not depend on the conjugate generalized coordinates
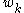
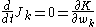
where the
are given by the typical equation for a type-2 canonical transformation
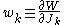
Hence, the new Hamiltonian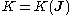
depends only on the new generalized momenta 
.
The dynamics of the action angles is given by Hamilton's equations
The right-hand side is a constant of the motion (since all the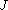
's are). Hence, the solution is given by
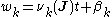
where
is a constant of integration. In particular, if the original generalized coordinate undergoes an oscillation or rotation of period 
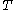, the corresponding action angle 
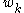changes by 
.
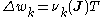These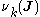
are the frequencies of oscillation/rotation for the original generalized coordinates 
. To show this, we integrate the net change in the action angle 
over exactly one complete variation (i.e., oscillation or rotation) of its generalized coordinates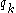 
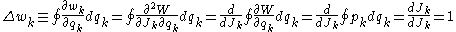
Setting the two expressions for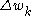
equal, we obtain the desired equation
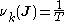
The action angles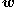
are an independent set of generalized coordinates
. Thus, in the general case, each original generalized coordinate
can be expressed as a Fourier series
in all the action angles
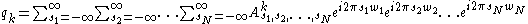
where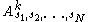
is the Fourier series coefficient. In most practical cases, however, an original generalized coordinate 
will be expressible as a Fourier series
in only its own action angles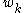
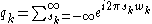
for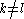 
. In such cases, the motion is called degenerate.
Degenerate motion signals that there are additional general conserved quantities; for example, the frequencies of the Kepler problem
are degenerate, corresponding to the conservation of the Laplace–Runge–Lenz vector.
Degenerate motion also signals that the Hamilton–Jacobi equation
s are completely separable in more than one coordinate system; for example, the Kepler problem is completely separable in both spherical coordinates and parabolic coordinates
.
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, action-angle coordinates are a set of canonical coordinates
Canonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
useful in solving many integrable system
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
s. The method of action-angles is useful for obtaining the frequencies
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
of oscillatory or rotational motion without solving the equations of motion. Action-angle coordinates are chiefly used when the Hamilton–Jacobi equation
Hamilton–Jacobi equation
In mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
s are completely separable. (Hence, the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
does not depend explicitly on time, i.e., the energy is conserved
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
.) Action-angle variables define an invariant torus, so called because holding the action constant defines the surface of a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, while the angle variables provide the coordinates on the torus.
The Bohr–Sommerfeld quantization conditions, used to develop quantum mechanics before the advent of wave mechanics, state that the action must be an integral multiple of Planck's constant; similarly, Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
's insight into EBK quantization and the difficulty of quantizing non-integrable systems was expressed in terms of the invariant tori of action-angle coordinates.
Action-angle coordinates are also useful in perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
of Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, especially in determining adiabatic invariant
Adiabatic invariant
An adiabatic invariant is a property of a physical system that stays constant when changes occur slowly.In thermodynamics, an adiabatic process is a change that occurs without heat flow, and slowly compared to the time to reach equilibrium. In an adiabatic process, the system is in equilibrium at...
s. One of the earliest results from chaos theory
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
, for the non-linear perturbations of dynamical systems with a small number of degrees of freedom is the KAM theorem, which states that the invariant tori are stable under small perturbations.
The use of action-angle variables was central to the solution of the Toda lattice, and to the definition of Lax pairs, or more generally, the idea of the isospectral
Isospectral
In mathematics, two linear operators are called isospectral or cospectral if they have the same spectrum. Roughly speaking, they are supposed to have the same sets of eigenvalues, when those are counted with multiplicity....
evolution of a system.
Derivation
Action angles result from a type-2 canonical transformationCanonical transformation
In Hamiltonian mechanics, a canonical transformation is a change of canonical coordinates → that preserves the form of Hamilton's equations , although it...
where the generating function is Hamilton's characteristic function
Hamilton–Jacobi equation
In mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
(not Hamilton's principal function ). Since the original Hamiltonian does not depend on time explicitly, the new Hamiltonian is merely the old Hamiltonian 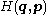expressed in terms of the new canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
, which we denote as
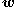(the action angles, which are the generalized coordinatesGeneralized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
) and their new generalized momenta
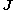. We will not need to solve here for the generating function itself; instead, we will use it merely as a vehicle for relating the new and old canonical coordinatesCanonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
.
Rather than defining the action angles
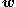directly, we define instead their generalized momenta, which resemble the classical actionAction (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
for each original generalized coordinate
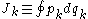
where the integration path is implicitly given by the constant energy function
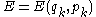. Since the actual motion is not involved in this integration, these generalized momenta 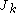are constants of the motion, implying that the transformed Hamiltonian 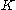does not depend on the conjugate generalized coordinatesGeneralized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
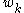
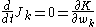
where the
are given by the typical equation for a type-2 canonical transformationCanonical transformation
In Hamiltonian mechanics, a canonical transformation is a change of canonical coordinates → that preserves the form of Hamilton's equations , although it...
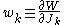
Hence, the new Hamiltonian
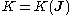depends only on the new generalized momenta .The dynamics of the action angles is given by Hamilton's equations
The right-hand side is a constant of the motion (since all the
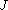's are). Hence, the solution is given by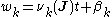where
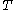is a constant of integration. In particular, if the original generalized coordinate undergoes an oscillation or rotation of period , the corresponding action angle 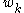changes by 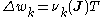.These
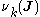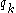
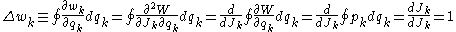
are the frequencies of oscillation/rotation for the original generalized coordinates . To show this, we integrate the net change in the action angle over exactly one complete variation (i.e., oscillation or rotation) of its generalized coordinates Setting the two expressions for
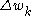equal, we obtain the desired equation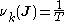The action angles
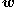are an independent set of generalized coordinatesGeneralized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
. Thus, in the general case, each original generalized coordinate
can be expressed as a Fourier seriesFourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
in all the action angles
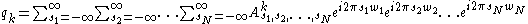
where
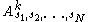is the Fourier series coefficient. In most practical cases, however, an original generalized coordinate will be expressible as a Fourier seriesFourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
in only its own action angles
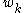
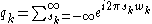
Summary of basic protocol
The general procedure has three steps:- Calculate the new generalized momenta
- Express the original Hamiltonian entirely in terms of these variables.
- Take the derivatives of the Hamiltonian with respect to these momenta to obtain the frequencies
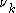
Degeneracy
In some cases, the frequencies of two different generalized coordinates are identical, i.e., for 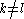. In such cases, the motion is called degenerate.Degenerate motion signals that there are additional general conserved quantities; for example, the frequencies of the Kepler problem
Kepler problem
In classical mechanics, the Kepler problem is a special case of the two-body problem, in which the two bodies interact by a central force F that varies in strength as the inverse square of the distance r between them. The force may be either attractive or repulsive...
are degenerate, corresponding to the conservation of the Laplace–Runge–Lenz vector.
Degenerate motion also signals that the Hamilton–Jacobi equation
Hamilton–Jacobi equation
In mathematics, the Hamilton–Jacobi equation is a necessary condition describing extremal geometry in generalizations of problems from the calculus of variations. In physics, the Hamilton–Jacobi equation is a reformulation of classical mechanics and, thus, equivalent to other formulations such as...
s are completely separable in more than one coordinate system; for example, the Kepler problem is completely separable in both spherical coordinates and parabolic coordinates
Parabolic coordinates
Parabolic coordinates are a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal parabolas. A three-dimensional version of parabolic coordinates is obtained by rotating the two-dimensional system about the symmetry axis of the parabolas.Parabolic coordinates have...
.