Parabolic coordinates
Encyclopedia
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
in which the coordinate lines are confocal
Confocal
In geometry, confocal means having the same foci.* For an optical cavity consisting of two mirrors, confocal means that they share their foci...
parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
s. A three-dimensional version
Parabolic cylindrical coordinates
In mathematics, parabolic cylindrical coordinates are a three-dimensional orthogonal coordinate system that results from projecting the two-dimensional parabolic coordinate system in the...
of parabolic coordinates is obtained by rotating the two-dimensional system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
about the symmetry axis of the parabolas.
Parabolic coordinates have found many applications, e.g., the treatment of the Stark effect
Stark effect
The Stark effect is the shifting and splitting of spectral lines of atoms and molecules due to presence of an external static electric field. The amount of splitting and or shifting is called the Stark splitting or Stark shift. In general one distinguishes first- and second-order Stark effects...
and the potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
of the edges.
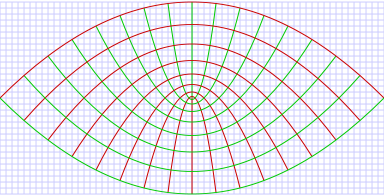
Two-dimensional parabolic coordinates
Two-dimensional parabolic coordinates
are defined by the equations
The curves of constant
form confocal parabolae
that open upwards (i.e., towards
), whereas the curves of constant 
form confocal parabolae
that open downwards (i.e., towards
). The foci of all these parabolae are located at the origin.Two-dimensional scale factors
The scale factors for the parabolic coordinates
are equal
Hence, the infinitesimal element of area is
and the Laplacian equals
Other differential operators such as
and
can be expressed in the coordinates 
by substitutingthe scale factors into the general formulae
found in orthogonal coordinates
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
.
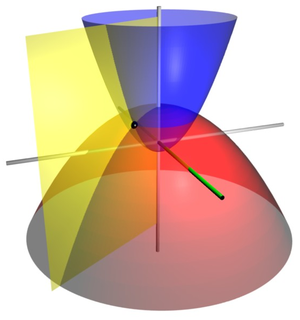
Three-dimensional parabolic coordinates
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
. The parabolic cylindrical coordinates
Parabolic cylindrical coordinates
In mathematics, parabolic cylindrical coordinates are a three-dimensional orthogonal coordinate system that results from projecting the two-dimensional parabolic coordinate system in the...
are produced by projecting in the
-direction.Rotation about the symmetry axis of the parabolae produces a set of
confocal paraboloids, forming a coordinate system that is also known as "parabolic coordinates"
where the parabolae are now aligned with the
-axis,about which the rotation was carried out. Hence, the azimuthal angle
is defined
The surfaces of constant
form confocal paraboloids
that open upwards (i.e., towards
) whereas the surfaces of constant 
form confocal paraboloids
that open downwards (i.e., towards
). The foci of all these paraboloids are located at the origin.The Riemannian
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
associated with this coordinate system is
Three-dimensional scale factors
The three dimensional scale factors are:
It is seen that The scale factors
and 
are the same as in the two-dimensional case. The infinitesimal volume element is then
and the Laplacian is given by
Other differential operators such as
and
can be expressed in the coordinates 
by substitutingthe scale factors into the general formulae
found in orthogonal coordinates
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
.