Parabolic cylindrical coordinates
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, parabolic cylindrical coordinates are a three-dimensional orthogonal
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
that results from projecting the two-dimensional parabolic coordinate system
Parabolic coordinates
Parabolic coordinates are a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal parabolas. A three-dimensional version of parabolic coordinates is obtained by rotating the two-dimensional system about the symmetry axis of the parabolas.Parabolic coordinates have...
in the
perpendicular
-direction. Hence, the coordinate surfaces are confocalConfocal
In geometry, confocal means having the same foci.* For an optical cavity consisting of two mirrors, confocal means that they share their foci...
parabolic
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
cylinders. Parabolic cylindrical coordinates have found many applications, e.g., the potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
of edges.
Basic definition
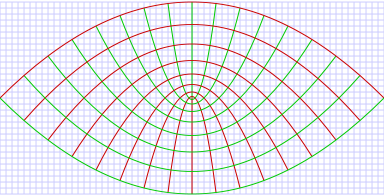
are defined in terms of the Cartesian coordinates (x,y,z) by: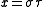
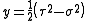
The surfaces of constant
form confocal parabolic cylinders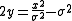
that open towards
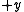, whereas the surfaces of constant 
form confocal parabolic cylinders
that open in the opposite direction, i.e., towards
. The foci of all these parabolic cylinders are located along the line defined by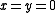 
. The radius r has a simple formula as well
that proves useful in solving the Hamilton-Jacobi equation in parabolic coordinates for the inverse-square
Inverse-square law
In physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....
central force problem of mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
; for further details, see the Laplace–Runge–Lenz vector article.
Scale factors
The scale factors for the parabolic cylindrical coordinates
and 
are: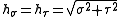
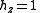
The infinitesimal element of volume is
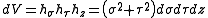
and the Laplacian equals
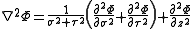
Other differential operators such as
and
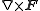can be expressed in the coordinates 
by substitutingthe scale factors into the general formulae
found in orthogonal coordinates
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
.
Parabolic cylinder harmonics
Since all of the surfaces of constant σ, τ and z are conicoid, Laplace's equation is separable in parabolic cylindrical coordinates. Using the technique of the separation of variablesSeparation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
, a separated solution to Laplace's equation may be written:
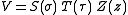
and Laplace's equation, divided by V , is written:
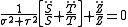
Since the Z equation is separate from the rest, we may write
where m is constant. Z(z) has the solution:
Substituting
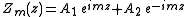for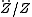 
, Laplace's equation may now be written:
We may now separate the S and T functions and introduce another constant
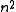to obtain: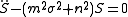
The solutions to these equations are the parabolic cylinder functions
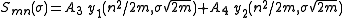
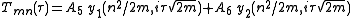
The parabolic cylinder harmonics for (m,n) are now the product of the solutions. The combination will reduce the number of constants and the general solution to Laplace's equation may be written:
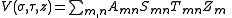
Applications
The classic applications of parabolic cylindrical coordinates are in solving partial differential equations,e.g., Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
or the Helmholtz equation
Helmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
, for which such coordinates allow a
separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
. A typical example would be the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
surrounding a
flat semi-infinite conducting plate.