|
|
|
|
Mechanics
|
| |
|
| |
Mechanics (Greek ) is the branch of physics concerned with the behaviour of physical bodies when subjected to forces or displacements, and the subsequent effect of the bodies on their environment.
The discipline has its roots in several ancient civilizations (see History of classical mechanics and Timeline of classical mechanics). During the early modern period, scientists such as Galileo, Kepler, and especially Newton, laid the foundation for what is now known as classical mechanics.
major division of the mechanics discipline separates classical mechanics from quantum mechanics.
Historically, classical mechanics came first, while quantum mechanics is a comparatively recent invention.
Discussion
Ask a question about 'Mechanics' Start a new discussion about 'Mechanics' Answer questions from other users |
Encyclopedia
Mechanics (Greek ) is the branch of physics concerned with the behaviour of physical bodies when subjected to forces or displacements, and the subsequent effect of the bodies on their environment.
The discipline has its roots in several ancient civilizations (see History of classical mechanics and Timeline of classical mechanics). During the early modern period, scientists such as Galileo, Kepler, and especially Newton, laid the foundation for what is now known as classical mechanics.
Classical versus quantum
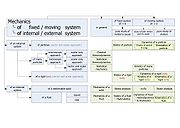
The major division of the mechanics discipline separates classical mechanics from quantum mechanics.
Historically, classical mechanics came first, while quantum mechanics is a comparatively recent invention. Classical mechanics originated with Isaac Newton's Laws of motion in Principia Mathematica, while quantum mechanics didn't appear until 1900. Both are commonly held to constitute the most certain knowledge that exists about physical nature. Classical mechanics has especially often been viewed as a model for other so-called exact sciences. Essential in this respect is the relentless use of mathematics in theories, as well as the decisive role played by experiment in generating and testing them.
Quantum mechanics is of a wider scope, as it encompasses classical mechanics as a sub-discipline which applies under certain restricted circumstances. According to the correspondence principle, there is no contradiction or conflict between the two subjects, each simply pertains to specific situations. Quantum mechanics has superseded classical mechanics at the foundational level and is indispensable for the explanation and prediction of processes at molecular and (sub)atomic level. However, for macroscopical processes classical mechanics is able to solve problems which are unmanageably difficult in quantum mechanics and hence remains useful and well used.
Einsteinian versus Newtonian
Analogous to the quantum versus classical reformation, Einstein's general and special theories of relativity have expanded the scope of mechanics beyond the mechanics of Newton and Galileo, and made fundamental corrections to them, that become significant and even dominant as speeds of material objects approach the speed of light, which cannot be exceeded. Relativistic corrections are also needed for quantum mechanics, although General relativity has not been integrated; the two theories remain incompatible, a hurdle which must be overcome in developing the Grand Unified Theory.
Types of mechanical bodies
Thus the often-used term body needs to stand for a wide assortment of objects, including particles, projectiles, spacecraft, stars, parts of machinery, parts of solids, parts of fluids (gases and liquids), etc.
Other distinctions between the various sub-disciplines of mechanics, concern the nature of the bodies being described. Particles are bodies with little (known) internal structure, treated as mathematical points in classical mechanics. Rigid bodies have size and shape, but retain a simplicity close to that of the particle, adding just a few so-called degrees of freedom, such as orientation in space.
Otherwise, bodies may be semi-rigid, i.e. elastic, or non-rigid, i.e. fluid. These subjects have both classical and quantum divisions of study.
For instance, the motion of a spacecraft, regarding its orbit and attitude (rotation), is described by the relativistic theory of classical mechanics, while the analogous movements of an atomic nucleus are described by quantum mechanics.
Sub-disciplines in mechanics
The following are two lists of various subjects that are studied in mechanics.
Note that there is also the "theory of fields" which constitutes a separate discipline in physics, formally treated as distinct from mechanics, whether classical fields or quantum fields. But in actual practice, subjects belonging to mechanics and fields are closely interwoven. Thus, for instance, forces that act on particles are frequently derived from fields (electromagnetic or gravitational), and particles generate fields by acting as sources. In fact, in quantum mechanics, particles themselves are fields, as described theoretically by the wave function.
Classical mechanics
The following are described as forming Classical mechanics:
- Newtonian mechanics, the original theory of motion (kinematics) and forces (dynamics)
- Hamiltonian mechanics, a theoretical formalism, based on the principle of conservation of energy
- Lagrangian mechanics, another theoretical formalism, based on the principle of the least action
- Celestial mechanics, the motion of heavenly bodies: planets, comets, stars, galaxies, etc.
- Astrodynamics, spacecraft navigation, etc.
- Solid mechanics, elasticity, the properties of (semi-)rigid bodies
- Acoustics, sound ( = density variation propagation) in solids, fluids and gases.
- Statics, semi-rigid bodies in mechanical equilibrium
- Fluid mechanics, the motion of fluids
- Soil mechanics, mechanical behavior of soils
- Continuum mechanics, mechanics of continua (both solid and fluid)
- Hydraulics, mechanical properties of liquids
- Fluid statics, liquids in equilibrium
- Applied mechanics, or Engineering mechanics
- Biomechanics, solids, fluids, etc. in biology
- Biophysics, physical processes in living organisms
- Statistical mechanics, assemblies of particles too large to be described in a deterministic way
- Relativistic or Einsteinian mechanics, universal gravitation
Quantum mechanics
The following are categorized as being part of Quantum mechanics:
- Particle physics, the motion, structure, and reactions of particles
- Nuclear physics, the motion, structure, and reactions of nuclei
- Condensed matter physics, quantum gases, solids, liquids, etc.
- Quantum statistical mechanics, large assemblies of particles
Professional organizations
See also
External links
-
-
-
- from the University of New South Wales
-
|
| |
|
|
