Acceleration
Encyclopedia
In physics
, acceleration is the rate of change of velocity
with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. Acceleration has the dimensions
L
T
−2. In SI
units, acceleration is measured in meters per second squared
(m/s2). (Negative acceleration i.e. retardation, also has the same dimensions/units.)
Proper acceleration
, the acceleration of a body relative to a free-fall condition, is measured by an instrument called an accelerometer
.
In common speech, the term acceleration is used for an increase in speed (the magnitude
of velocity); a decrease in speed is called deceleration. In physics, a change in the direction of velocity also is an acceleration: for rotary motion, the change in direction of velocity results in centripetal (toward the center) acceleration; whereas the rate of change of speed is a tangential acceleration.
In classical mechanics
, for a body with constant mass, the acceleration of the body is proportional to the net force acting on it (Newton's second law
):
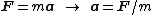
where F is the resultant force acting on the body, m is the mass of the body, and a is its acceleration.
Average acceleration is the change in velocity (Δv) divided by the change in time (Δt). Instantaneous acceleration is the acceleration at a specific point in time which is for a very short interval of time as Δt approaches zero.
The velocity of a particle moving on a curved path as a function
of time can be written as: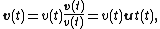
with v(t) equal to the speed of travel along the path, and
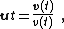
a unit vector tangent to the path pointing in the direction of motion at the chosen moment in time. Taking into account both the changing speed v(t) and the changing direction of ut, the acceleration of a particle moving on a curved path on a planar surface can be written using the chain rule
of differentiation and the derivative of the product of two functions of time as:
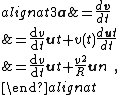
where un is the unit (inward) normal vector to the particle's trajectory, and R is its instantaneous radius of curvature based upon the osculating circle at time t. These components are called the tangential acceleration and the radial acceleration or centripetal acceleration (see also circular motion
and centripetal force
).
Extension of this approach to three-dimensional space curves that cannot be contained on a planar surface leads to the Frenet–Serret formulas.
of an object changes by an equal amount in every equal time period.
A frequently cited example of uniform acceleration is that of an object in free fall
in a uniform gravitational field. The acceleration of a falling body in the absence of resistances to motion is dependent only on the gravitational field
strength g
(also called acceleration due to gravity). By Newton's Second Law the force
, F, acting on a body is given by:
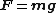
Due to the simple algebraic properties of constant acceleration in the one-dimensional case (that is, the case of acceleration aligned with the initial velocity), there are simple formulas that relate the following quantities: displacement
, initial velocity
, final velocity, acceleration, and time
:
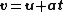
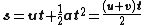
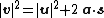
where
= displacement
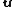= initial velocity
= final velocity
= uniform acceleration
= time.
In the case of uniform acceleration of an object that is initially moving in a direction not aligned with the acceleration, the motion can be resolved into two orthogonal parts, one of constant velocity and the other according to the above equations. As Galileo showed, the net result is parabolic motion, as in the trajectory of a cannonball, neglecting air resistance.
. In this case, because the direction of the object's motion is constantly changing, being tangential to the circle, the object's velocity
also changes, but its speed does not. This acceleration is directed toward the centre of the circle and takes the value:
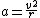
where v is the object's speed
. Equivalently, the radial acceleration may be calculated from the object's angular velocity
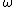, whence:
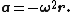
The acceleration, hence also the force acting on a body in uniform circular motion, is directed toward the center of the circle; that is, it is centripetal
– the so called 'centrifugal force
' appearing to act outward on a body is really a pseudo force experienced in the frame of reference
of the body in circular motion, due to the body's linear momentum at a tangent to the circle.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, acceleration is the rate of change of velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. Acceleration has the dimensions
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
L
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
T
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
−2. In SI
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
units, acceleration is measured in meters per second squared
(m/s2). (Negative acceleration i.e. retardation, also has the same dimensions/units.)
Proper acceleration
Proper acceleration
In relativity theory, proper acceleration is the physical acceleration experienced by an object. It is acceleration relative to a free-fall, or inertial, observer who is momentarily at rest relative to the object being measured...
, the acceleration of a body relative to a free-fall condition, is measured by an instrument called an accelerometer
Accelerometer
An accelerometer is a device that measures proper acceleration, also called the four-acceleration. This is not necessarily the same as the coordinate acceleration , but is rather the type of acceleration associated with the phenomenon of weight experienced by a test mass that resides in the frame...
.
In common speech, the term acceleration is used for an increase in speed (the magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
of velocity); a decrease in speed is called deceleration. In physics, a change in the direction of velocity also is an acceleration: for rotary motion, the change in direction of velocity results in centripetal (toward the center) acceleration; whereas the rate of change of speed is a tangential acceleration.
In classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, for a body with constant mass, the acceleration of the body is proportional to the net force acting on it (Newton's second law
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
):
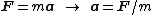
where F is the resultant force acting on the body, m is the mass of the body, and a is its acceleration.
Average acceleration is the change in velocity (Δv) divided by the change in time (Δt). Instantaneous acceleration is the acceleration at a specific point in time which is for a very short interval of time as Δt approaches zero.
Tangential and centripetal acceleration
The velocity of a particle moving on a curved path as a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of time can be written as:
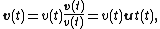
with v(t) equal to the speed of travel along the path, and
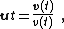
a unit vector tangent to the path pointing in the direction of motion at the chosen moment in time. Taking into account both the changing speed v(t) and the changing direction of ut, the acceleration of a particle moving on a curved path on a planar surface can be written using the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
of differentiation and the derivative of the product of two functions of time as:
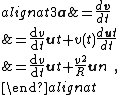
where un is the unit (inward) normal vector to the particle's trajectory, and R is its instantaneous radius of curvature based upon the osculating circle at time t. These components are called the tangential acceleration and the radial acceleration or centripetal acceleration (see also circular motion
Circular motion
In physics, circular motion is rotation along a circular path or a circular orbit. It can be uniform, that is, with constant angular rate of rotation , or non-uniform, that is, with a changing rate of rotation. The rotation around a fixed axis of a three-dimensional body involves circular motion of...
and centripetal force
Centripetal force
Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
).
Extension of this approach to three-dimensional space curves that cannot be contained on a planar surface leads to the Frenet–Serret formulas.
Uniform acceleration
Uniform or constant acceleration is a type of motion in which the velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of an object changes by an equal amount in every equal time period.
A frequently cited example of uniform acceleration is that of an object in free fall
Free fall
Free fall is any motion of a body where gravity is the only force acting upon it, at least initially. These conditions produce an inertial trajectory so long as gravity remains the only force. Since this definition does not specify velocity, it also applies to objects initially moving upward...
in a uniform gravitational field. The acceleration of a falling body in the absence of resistances to motion is dependent only on the gravitational field
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
strength g
Standard gravity
Standard gravity, or standard acceleration due to free fall, usually denoted by g0 or gn, is the nominal acceleration of an object in a vacuum near the surface of the Earth. It is defined as precisely , or about...
(also called acceleration due to gravity). By Newton's Second Law the force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
, F, acting on a body is given by:
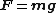
Due to the simple algebraic properties of constant acceleration in the one-dimensional case (that is, the case of acceleration aligned with the initial velocity), there are simple formulas that relate the following quantities: displacement
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
, initial velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
, final velocity, acceleration, and time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
:
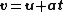
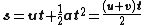
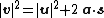
where
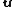= displacement = initial velocity = final velocity = uniform acceleration = time.In the case of uniform acceleration of an object that is initially moving in a direction not aligned with the acceleration, the motion can be resolved into two orthogonal parts, one of constant velocity and the other according to the above equations. As Galileo showed, the net result is parabolic motion, as in the trajectory of a cannonball, neglecting air resistance.
Circular motion
An example of a body experiencing acceleration of a uniform magnitude but changing direction is uniform circular motionCircular motion
In physics, circular motion is rotation along a circular path or a circular orbit. It can be uniform, that is, with constant angular rate of rotation , or non-uniform, that is, with a changing rate of rotation. The rotation around a fixed axis of a three-dimensional body involves circular motion of...
. In this case, because the direction of the object's motion is constantly changing, being tangential to the circle, the object's velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
also changes, but its speed does not. This acceleration is directed toward the centre of the circle and takes the value:
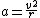
where v is the object's speed
Speed
In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
. Equivalently, the radial acceleration may be calculated from the object's angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
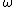, whence: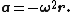The acceleration, hence also the force acting on a body in uniform circular motion, is directed toward the center of the circle; that is, it is centripetal
Centripetal force
Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
– the so called 'centrifugal force
Centrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
' appearing to act outward on a body is really a pseudo force experienced in the frame of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
of the body in circular motion, due to the body's linear momentum at a tangent to the circle.
Relation to relativity
"The force one feels from gravity and the force one feels from acceleration are the same. They are equivalent. Einstein called this the principle of equivalence. Since gravity and acceleration are equivalent, if you feel gravity's influence, you must be accelerating. Einstein argued that only those observers who feel no force at all - including the force of gravity - are justified in declaring that they are not accelerating."See also
- Angular accelerationAngular accelerationAngular acceleration is the rate of change of angular velocity over time. In SI units, it is measured in radians per second squared , and is usually denoted by the Greek letter alpha .- Mathematical definition :...
- Gravitational accelerationGravitational accelerationIn physics, gravitational acceleration is the acceleration on an object caused by gravity. Neglecting friction such as air resistance, all small bodies accelerate in a gravitational field at the same rate relative to the center of mass....
- KinematicsKinematicsKinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
- Equations of motion
- Proper accelerationProper accelerationIn relativity theory, proper acceleration is the physical acceleration experienced by an object. It is acceleration relative to a free-fall, or inertial, observer who is momentarily at rest relative to the object being measured...
- 0 to 60 mph0 to 60 mphThe time it takes to accelerate from 0 to 60 mph is a commonly used performance measure for automotive acceleration in the United States and the United Kingdom. In the rest of the world 0 to 100 km/h is used...
(0 to 100 km/h) - Shock (mechanics)Shock (mechanics)A mechanical or physical shock is a sudden acceleration or deceleration caused, for example, by impact, drop, kick, earthquake, or explosion. Shock is a transient physical excitation....
- Specific force
External links
- Acceleration Calculator Simple acceleration unit converter
- Measurespeed.com - Acceleration Calculator Based on starting & ending speed and time elapsed.