Lagrangian mechanics
Encyclopedia
Lagrangian mechanics is a re-formulation of classical mechanics
that combines conservation of momentum with conservation of energy
. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange
in 1788.
In Lagrangian mechanics, the trajectory of a system of particles is derived by solving the Lagrange equations in one of two forms, either the Lagrange equations of the first kind, which treat constraints explicitly as extra equations, often using Lagrange multipliers
; or the Lagrange equations of the second kind, which incorporate the constraints directly by judicious choice of generalized coordinates
. The fundamental lemma of the calculus of variations shows that solving the Lagrange equations is equivalent to finding the path for which the action functional
is stationary, a quantity that is the integral
of the Lagrangian
over time.
The use of generalized coordinates may considerably simplify a system's analysis
. For example, consider a small frictionless bead traveling in a groove. If one is tracking the bead as a particle, calculation of the motion of the bead using Newtonian mechanics would require solving for the time-varying constraint force required to keep the bead in the groove. For the same problem using Lagrangian mechanics, one looks at the path of the groove and chooses a set of independent generalized coordinates that completely characterize the possible motion of the bead. This choice eliminates the need for the constraint force to enter into the resultant system of equations. There are fewer equations since one is not directly calculating the influence of the groove on the bead at a given moment. [This does not appear to be true, since using standard Newtonian mechanics one would ignore an analysis of forces and use conservation of energy which follows directly from Newton's laws; alternatively one can eliminate the constraint force by resolving tangentially to the groove].
is used rather than 
for potential energy and 
replaces 
for kinetic energy. See the references for more detailed and more general derivations.
Start with D'Alembert's principle
for the virtual work
of applied forces,
, and inertia
l forces on a three dimensional accelerating system of
particles, 
, whose motion is consistent with its constraints,
where
is the virtual work;
is the virtual displacement of the system, consistent with the constraints;
are the masses of the particles in the system;
are the accelerations of the particles in the system;
together as products represent the time derivatives of the system momenta, aka. inertial forces;
is an integer used to indicate (via subscript) a variable corresponding to a particular particle; and
is the number of particles under consideration.
Break out the two terms:
Assume that the following transformation equations from m independent generalized coordinates
,
, hold:
where m (without a subscript) indicates the total number of generalized coordinates. An expression for the virtual displacement (differential),
of the system for time-independent constraints or "velocity-dependent constraints" is
where
is an integer used to indicate (via subscript) a variable corresponding to a generalized coordinate.
The applied forces may be expressed in the generalized coordinates as generalized forces,
:
Combining the equations for
, 
, and 
yields the following result after pulling the sum out of the dot product in the second term:
Substituting in the result from the kinetic energy relations to change the inertial forces into a function of the kinetic energy leaves
In the above equation,
is arbitrary, though it is by definition consistent with the constraints. So the relation must hold term-wise:
If the
are conservative
, they may be represented by a scalar potential
field,
:
The previous result may be easier to see by recognizing that
is a function of the 
, which are in turn functions of 
, and then applying the chain rule
to the derivative of
with respect to 
.
Recall the definition of the Lagrangian
is
Since the potential field is only a function of position, not velocity, Lagrange's equations are as follows:
This is consistent with the results derived above and may be seen by differentiating the right side of the Lagrangian with respect to
and time, and solely with respect to 
, adding the results and associating terms with the equations for 
and 
.
In a more general formulation, the forces could be both potential and viscous
. If an appropriate transformation can be found from the
, Rayleigh
suggests using a dissipation function,
, of the following form:
where
are constants that are related to the damping coefficients in the physical system, though not necessarily equal to them
If
is defined this way, then
and
,
, for the system of particles is defined by
The partial derivative of
with respect to the time derivative
s of the generalized coordinates,
, is
The previous result may be difficult to visualize. As a result of the product rule
, the derivative of a general dot product
is
This general result may be seen by briefly stepping into a Cartesian coordinate system
, recognizing that the dot product is (there) a term-by-term product sum, and also recognizing that the derivative of a sum is the sum of its derivatives. In our case,
and 
are equal to 
, which is why the factor of one half disappears.
According to the chain rule
and the coordinate transformation equations given above for
, its time derivative, 
, is
Together, the definition of
and the total differential, 
, suggest that
since
and that in the sum, there is only one
Substituting this relation back into the expression for the partial derivative of
gives
Taking the time derivative gives
Using the chain rule on the last term gives
From the expression for
, one sees that also
This allows simplification of the last term,
The partial derivative of
with respect to the generalized coordinates, 
, is
This last result may be obtained by doing a partial differentiation directly on the kinetic energy definition represented by the first equation. The last two equations may be combined to give an expression for the inertial forces in terms of the kinetic energy:
m and position vector
, moving under an applied force
,
, which can be expressed as the gradient
of a scalar potential energy function
:
Such a force is independent of third- or higher-order derivatives of
, so Newton's second law
forms a set of 3 second-order ordinary differential equation
s. Therefore, the motion of the particle can be completely described by 6 independent variables, or degrees of freedom. An obvious set of variables is
, the Cartesian components of 
and their time derivatives, at a given instant of time (i.e. position (x,y,z) and velocity 
).
More generally, we can work with a set of generalized coordinates
,
, and their time derivatives, the generalized velocities, 
. The position vector, 
, is related to the generalized coordinates by some transformation equation:
For example, for a simple pendulum of length ℓ, a logical choice for a generalized coordinate is the angle of the pendulum from vertical, θ, for which the transformation equation would be
The term "generalized coordinates" is really a holdover from the period when Cartesian coordinates
were the default coordinate system.
Consider an arbitrary displacement
of the particle. The work
done by the applied force
is 
. Using Newton's second law, we write:
Since work is a physical scalar quantity, we should be able to rewrite this equation in terms of the generalized coordinates and velocities. On the left hand side,
On the right hand side, carrying out a change of coordinates to generalized coordinates, we obtain:
Rearranging slightly:
Now, by performing an "integration by parts" transformation, with respect to t:
Recognizing that
and 
, we obtain:
Now, by changing the order of differentiation, we obtain:
Finally, we change the order of summation:
Which is equivalent to:
where
is the kinetic energy of the particle. Our equation for the work done becomes
However, this must be true for any set of generalized displacements
, so we must have
for each generalized coordinate
. We can further simplify this by noting that V is a function solely of r and t, and r is a function of the generalized coordinates and t. Therefore, V is independent of the generalized velocities:
Inserting this into the preceding equation and substituting L = T − V, called the Lagrangian, we obtain Lagrange's equations:
There is one Lagrange equation for each generalized coordinate qi. When qi = ri (i.e. the generalized coordinates are simply the Cartesian coordinates), it is straightforward to check that Lagrange's equations reduce to Newton's second law.
The above derivation can be generalized to a system of N particles. There will be 6N generalized coordinates, related to the position coordinates by 3N transformation equations. In each of the 3N Lagrange equations, T is the total kinetic energy of
the system, and V the total potential energy.
In practice, it is often easier to solve a problem using the Euler–Lagrange equations than Newton's laws. This is because not only may more appropriate generalized coordinates qi be chosen to exploit symmetries in the system, but constraint forces are replaced with simpler relations.
from which the solution
follows (choosing the origin at the starting point). This result can also be derived through the Lagrangian formalism. Take x to be the coordinate, which is 0 at the starting point. The kinetic energy is T = mv2 and the potential energy is V = −mgx; hence,
.
Then
which can be rewritten as
, yielding the same result as earlier.
The kinetic energy can then be shown to be
and the potential energy of the system is
The Lagrangian is therefore
Now carrying out the differentiations gives for the support coordinate x
therefore:
indicating the presence of a constant of motion. Performing the same procedure for the variable
yields:
therefore
These equations may look quite complicated, but finding them with Newton's laws would have required carefully identifying all forces, which would have been much harder and more prone to errors. By considering limit cases (for example,
should give the equations of motion for a pendulum which is at rest in some inertial frame, while 
should give the equations for a pendulum in a constantly accelerating system, etc.) the correctness of this system can be verified. Furthermore, it is trivial to obtain the results numerically, given suitable starting conditions and a chosen time step, by stepping through the results iteratively
.
are introduced; namely, the location of the center of mass R and the separation of the bodies r (the relative position). The Lagrangian is then
where M is the total mass, μ is the reduced mass, and U the potential of the radial force. The Lagrangian is divided into a center-of-mass term and a relative motion term. The R equation from the Euler-Lagrange system is simply:
resulting in simple motion of the center of mass in a straight line at constant velocity. The relative motion is expressed in polar coordinates (r, θ):
which does not depend upon θ, therefore an ignorable coordinate. The Lagrange equation for θ is then:
where ℓ is the conserved angular momentum. The Lagrange equation for r is:
or:
This equation is identical to the radial equation obtained using Newton's laws in a co-rotating reference frame, that is, a frame rotating with the reduced mass so it appears stationary. If the angular velocity is replaced by its value in terms of the angular momentum,
the radial equation becomes:
which is the equation of motion for a one-dimensional problem in which a particle of mass μ is subjected to the inward central force −dU/dr and a second outward force, called in this context the centrifugal force
:
Of course, if one remains entirely within the one-dimensional formulation, ℓ enters only as some imposed parameter of the external outward force, and its interpretation as angular momentum depends upon the more general two-dimensional problem from which the one-dimensional problem originated.
If one arrives at this equation using Newtonian mechanics in a co-rotating frame, the interpretation is evident as the centrifugal force in that frame due to the rotation of the frame itself. If one arrives at this equation directly by using the generalized coordinates (r, θ) and simply following the Lagrangian formulation without thinking about frames at all, the interpretation is that the centrifugal force is an outgrowth of using polar coordinates. As Hildebrand says: "Since such quantities are not true physical forces, they are often called inertia forces. Their presence or absence depends, not upon the particular problem at hand, but upon the coordinate system chosen." In particular, if Cartesian coordinates are chosen, the centrifugal force disappears, and the formulation involves only the central force itself, which provides the centripetal force
for a curved motion.
This viewpoint, that fictitious forces originate in the choice of coordinates, often is expressed by users of the Lagrangian method. This view arises naturally in the Lagrangian approach, because the frame of reference is (possibly unconsciously) selected by the choice of coordinates. Unfortunately, this usage of "inertial force" conflicts with the Newtonian idea of an inertial force. In the Newtonian view, an inertial force originates in the acceleration of the frame of observation (the fact that it is not an inertial frame of reference
), not in the choice of coordinate system. To keep matters clear, it is safest to refer to the Lagrangian inertial forces as generalized inertial forces, to distinguish them from the Newtonian vector inertial forces. That is, one should avoid following Hildebrand when he says (p. 155) "we deal always with generalized forces, velocities accelerations, and momenta. For brevity, the adjective "generalized" frequently will be omitted."
It is known that the Lagrangian of a system is not unique. Within the Lagrangian formalism the Newtonian fictitious forces can be identified by the existence of alternative Lagrangians in which the fictitious forces disappear, sometimes found by exploiting the symmetry of the system.
, is the time integral of the Lagrangian:
Let q0 and q1 be the coordinates at respective initial and final times t0 and t1. Using the calculus of variations
, it can be shown the Lagrange's equations are equivalent to Hamilton's principle
:
By stationary, we mean that the action does not vary to first-order for infinitesimal deformations of the trajectory, with the end-points (q0, t0) and (q1,t1) fixed. Hamilton's principle can be written as:
Thus, instead of thinking about particles accelerating in response to applied forces, one might think of them picking out the path with a stationary action.
Hamilton's principle is sometimes referred to as the principle of least action
. However, this is a misnomer: the action only needs to be stationary, with any variation h of the functional giving an increase in the functional integral of the action. This is not, as is frequently misstated, required to be a maximum or a minimum of the action functional.
We can use this principle instead of Newton's Laws as the fundamental principle of mechanics, this allows us to use an integral principle (Newton's Laws are based on differential equations so they are a differential principle) as the basis for mechanics. However it is not widely stated that Hamilton's principle is a variational principle only with holonomic
constraints, if we are dealing with nonholonomic systems then the variational principle should be replaced with one involving d'Alembert principle of virtual work
. Working only with holonomic constraints is the price we have to pay for using an elegant variational formulation of mechanics.
, denoted by H, is obtained by performing a Legendre transformation
on the Lagrangian, which introduces new variables, canonically conjugate to the original variables. This doubles the number of variables, but makes differential equations first order. The Hamiltonian is the basis for an alternative formulation of classical mechanics known as Hamiltonian mechanics
. It is a particularly ubiquitous quantity in quantum mechanics
(see Hamiltonian (quantum mechanics)
).
In 1948, Feynman
discovered the path integral formulation
extending the principle of least action
to quantum mechanics
for electrons and photons. In this formulation, particles travel every possible path between the initial and final states; the probability of a specific final state is obtained by summing over all possible trajectories leading to it. In the classical regime, the path integral formulation cleanly reproduces Hamilton's principle, and Fermat's principle
in optics
.
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
that combines conservation of momentum with conservation of energy
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange
Lagrange
La Grange literally means the barn in French. Lagrange may refer to:- People :* Charles Varlet de La Grange , French actor* Georges Lagrange , translator to and writer in Esperanto...
in 1788.
In Lagrangian mechanics, the trajectory of a system of particles is derived by solving the Lagrange equations in one of two forms, either the Lagrange equations of the first kind, which treat constraints explicitly as extra equations, often using Lagrange multipliers
Lagrange multipliers
In mathematical optimization, the method of Lagrange multipliers provides a strategy for finding the maxima and minima of a function subject to constraints.For instance , consider the optimization problem...
; or the Lagrange equations of the second kind, which incorporate the constraints directly by judicious choice of generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
. The fundamental lemma of the calculus of variations shows that solving the Lagrange equations is equivalent to finding the path for which the action functional
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
is stationary, a quantity that is the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
over time.
The use of generalized coordinates may considerably simplify a system's analysis
Analysis
Analysis is the process of breaking a complex topic or substance into smaller parts to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle , though analysis as a formal concept is a relatively recent development.The word is...
. For example, consider a small frictionless bead traveling in a groove. If one is tracking the bead as a particle, calculation of the motion of the bead using Newtonian mechanics would require solving for the time-varying constraint force required to keep the bead in the groove. For the same problem using Lagrangian mechanics, one looks at the path of the groove and chooses a set of independent generalized coordinates that completely characterize the possible motion of the bead. This choice eliminates the need for the constraint force to enter into the resultant system of equations. There are fewer equations since one is not directly calculating the influence of the groove on the bead at a given moment. [This does not appear to be true, since using standard Newtonian mechanics one would ignore an analysis of forces and use conservation of energy which follows directly from Newton's laws; alternatively one can eliminate the constraint force by resolving tangentially to the groove].
Lagrange equations of the second kind
The equations of motion in Lagrangian mechanics are the Lagrange equations, also known as the Euler–Lagrange equations. In lagrange equation there are 2n Generalized coordinates. Below, we sketch out the derivation of the Lagrange equations of the second kind. Please note that in this context, is used rather than for potential energy and replaces for kinetic energy. See the references for more detailed and more general derivations.Start with D'Alembert's principle
D'Alembert's principle
D'Alembert's principle, also known as the Lagrange–d'Alembert principle, is a statement of the fundamental classical laws of motion. It is named after its discoverer, the French physicist and mathematician Jean le Rond d'Alembert...
for the virtual work
Virtual work
Virtual work arises in the application of the principle of least action to the study of forces and movement of a mechanical system. Historically, virtual work and the associated calculus of variations were formulated to analyze systems of rigid bodies, but they have also been developed for the...
of applied forces,
, and inertiaInertia
Inertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion. It is proportional to an object's mass. The principle of inertia is one of the fundamental principles of classical physics which are used to...
l forces on a three dimensional accelerating system of
particles, , whose motion is consistent with its constraints,where
is the virtual work; is the virtual displacement of the system, consistent with the constraints; are the masses of the particles in the system; are the accelerations of the particles in the system; together as products represent the time derivatives of the system momenta, aka. inertial forces; is an integer used to indicate (via subscript) a variable corresponding to a particular particle; and is the number of particles under consideration.Break out the two terms:
Assume that the following transformation equations from m independent generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
,
, hold:where m (without a subscript) indicates the total number of generalized coordinates. An expression for the virtual displacement (differential),
of the system for time-independent constraints or "velocity-dependent constraints" iswhere
is an integer used to indicate (via subscript) a variable corresponding to a generalized coordinate.The applied forces may be expressed in the generalized coordinates as generalized forces,
:Combining the equations for
, , and yields the following result after pulling the sum out of the dot product in the second term:Substituting in the result from the kinetic energy relations to change the inertial forces into a function of the kinetic energy leaves
In the above equation,
is arbitrary, though it is by definition consistent with the constraints. So the relation must hold term-wise:If the
are conservativeConservative force
A conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the net work done by a conservative force is zero.It is possible to define a numerical value of...
, they may be represented by a scalar potential
Scalar potential
A scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
field,
:The previous result may be easier to see by recognizing that
is a function of the , which are in turn functions of , and then applying the chain ruleChain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
to the derivative of
with respect to .Recall the definition of the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
is
Since the potential field is only a function of position, not velocity, Lagrange's equations are as follows:
This is consistent with the results derived above and may be seen by differentiating the right side of the Lagrangian with respect to
and time, and solely with respect to , adding the results and associating terms with the equations for and .In a more general formulation, the forces could be both potential and viscous
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
. If an appropriate transformation can be found from the
, RayleighJohn Strutt, 3rd Baron Rayleigh
John William Strutt, 3rd Baron Rayleigh, OM was an English physicist who, with William Ramsay, discovered the element argon, an achievement for which he earned the Nobel Prize for Physics in 1904...
suggests using a dissipation function,
, of the following form:where
are constants that are related to the damping coefficients in the physical system, though not necessarily equal to themIf
is defined this way, thenand
Kinetic energy relations
The kinetic energyKinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
,
, for the system of particles is defined byThe partial derivative of
with respect to the time derivativeTime derivative
A time derivative is a derivative of a function with respect to time, usually interpreted as the rate of change of the value of the function. The variable denoting time is usually written as t\,.-Notation:...
s of the generalized coordinates,
, isThe previous result may be difficult to visualize. As a result of the product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
, the derivative of a general dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
is
This general result may be seen by briefly stepping into a Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
, recognizing that the dot product is (there) a term-by-term product sum, and also recognizing that the derivative of a sum is the sum of its derivatives. In our case,
and are equal to , which is why the factor of one half disappears.According to the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
and the coordinate transformation equations given above for
, its time derivative, , isTogether, the definition of
and the total differential, , suggest thatsince
and that in the sum, there is only one
Substituting this relation back into the expression for the partial derivative of
givesTaking the time derivative gives
Using the chain rule on the last term gives
From the expression for
, one sees that alsoThis allows simplification of the last term,
The partial derivative of
with respect to the generalized coordinates, , isThis last result may be obtained by doing a partial differentiation directly on the kinetic energy definition represented by the first equation. The last two equations may be combined to give an expression for the inertial forces in terms of the kinetic energy:
Old Lagrange's equations
Consider a single particle with massMass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
m and position vector
, moving under an applied forceForce
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
,
, which can be expressed as the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of a scalar potential energy function
:Such a force is independent of third- or higher-order derivatives of
, so Newton's second lawNewton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
forms a set of 3 second-order ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s. Therefore, the motion of the particle can be completely described by 6 independent variables, or degrees of freedom. An obvious set of variables is
, the Cartesian components of and their time derivatives, at a given instant of time (i.e. position (x,y,z) and velocity ).More generally, we can work with a set of generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
,
, and their time derivatives, the generalized velocities, . The position vector, , is related to the generalized coordinates by some transformation equation:For example, for a simple pendulum of length ℓ, a logical choice for a generalized coordinate is the angle of the pendulum from vertical, θ, for which the transformation equation would be
The term "generalized coordinates" is really a holdover from the period when Cartesian coordinates
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
were the default coordinate system.
Consider an arbitrary displacement
of the particle. The workMechanical work
In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
done by the applied force
is . Using Newton's second law, we write:Since work is a physical scalar quantity, we should be able to rewrite this equation in terms of the generalized coordinates and velocities. On the left hand side,
On the right hand side, carrying out a change of coordinates to generalized coordinates, we obtain:
Rearranging slightly:
Now, by performing an "integration by parts" transformation, with respect to t:
Recognizing that
and , we obtain:Now, by changing the order of differentiation, we obtain:
Finally, we change the order of summation:
Which is equivalent to:
where
is the kinetic energy of the particle. Our equation for the work done becomesHowever, this must be true for any set of generalized displacements
, so we must havefor each generalized coordinate
. We can further simplify this by noting that V is a function solely of r and t, and r is a function of the generalized coordinates and t. Therefore, V is independent of the generalized velocities:Inserting this into the preceding equation and substituting L = T − V, called the Lagrangian, we obtain Lagrange's equations:
There is one Lagrange equation for each generalized coordinate qi. When qi = ri (i.e. the generalized coordinates are simply the Cartesian coordinates), it is straightforward to check that Lagrange's equations reduce to Newton's second law.
The above derivation can be generalized to a system of N particles. There will be 6N generalized coordinates, related to the position coordinates by 3N transformation equations. In each of the 3N Lagrange equations, T is the total kinetic energy of
the system, and V the total potential energy.
In practice, it is often easier to solve a problem using the Euler–Lagrange equations than Newton's laws. This is because not only may more appropriate generalized coordinates qi be chosen to exploit symmetries in the system, but constraint forces are replaced with simpler relations.
Examples
In this section two examples are provided in which the above concepts are applied. The first example establishes that in a simple case, the Newtonian approach and the Lagrangian formalism agree. The second case illustrates the power of the above formalism, in a case which is hard to solve with Newton's laws.Falling mass
Consider a point mass m falling freely from rest. By gravity a force F = mg is exerted on the mass (assuming g constant during the motion). Filling in the force in Newton's law, we find from which the solutionfollows (choosing the origin at the starting point). This result can also be derived through the Lagrangian formalism. Take x to be the coordinate, which is 0 at the starting point. The kinetic energy is T = mv2 and the potential energy is V = −mgx; hence,
.Then
which can be rewritten as
, yielding the same result as earlier.Pendulum on a movable support
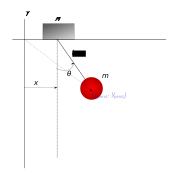
Consider a pendulum of mass m and length ℓ, which is attached to a support with mass M which can move along a line in the x-direction. Let x be the coordinate along the line of the support, and let us denote the position of the pendulum by the angle θ from the vertical.and the potential energy of the system is
The Lagrangian is therefore
Now carrying out the differentiations gives for the support coordinate x
therefore:
indicating the presence of a constant of motion. Performing the same procedure for the variable
yields:therefore
These equations may look quite complicated, but finding them with Newton's laws would have required carefully identifying all forces, which would have been much harder and more prone to errors. By considering limit cases (for example,
should give the equations of motion for a pendulum which is at rest in some inertial frame, while should give the equations for a pendulum in a constantly accelerating system, etc.) the correctness of this system can be verified. Furthermore, it is trivial to obtain the results numerically, given suitable starting conditions and a chosen time step, by stepping through the results iterativelyNumerical ordinary differential equations
Numerical ordinary differential equations is the part of numerical analysis which studies the numerical solution of ordinary differential equations...
.
Two-body central force problem
The basic problem is that of two bodies in orbit about each other attracted by a central force. The Jacobi coordinatesJacobi coordinates
In the theory of many-particle systems, Jacobi coordinates often are used to simplify the mathematical formulation. These coordinates are particularly common in treating polyatomic molecules and chemical reactions, and in celestial mechanics. An algorithm for generating the Jacobi coordinates for...
are introduced; namely, the location of the center of mass R and the separation of the bodies r (the relative position). The Lagrangian is then
where M is the total mass, μ is the reduced mass, and U the potential of the radial force. The Lagrangian is divided into a center-of-mass term and a relative motion term. The R equation from the Euler-Lagrange system is simply:
resulting in simple motion of the center of mass in a straight line at constant velocity. The relative motion is expressed in polar coordinates (r, θ):
which does not depend upon θ, therefore an ignorable coordinate. The Lagrange equation for θ is then:
where ℓ is the conserved angular momentum. The Lagrange equation for r is:
or:
This equation is identical to the radial equation obtained using Newton's laws in a co-rotating reference frame, that is, a frame rotating with the reduced mass so it appears stationary. If the angular velocity is replaced by its value in terms of the angular momentum,
the radial equation becomes:
which is the equation of motion for a one-dimensional problem in which a particle of mass μ is subjected to the inward central force −dU/dr and a second outward force, called in this context the centrifugal force
Centrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
:
Of course, if one remains entirely within the one-dimensional formulation, ℓ enters only as some imposed parameter of the external outward force, and its interpretation as angular momentum depends upon the more general two-dimensional problem from which the one-dimensional problem originated.
If one arrives at this equation using Newtonian mechanics in a co-rotating frame, the interpretation is evident as the centrifugal force in that frame due to the rotation of the frame itself. If one arrives at this equation directly by using the generalized coordinates (r, θ) and simply following the Lagrangian formulation without thinking about frames at all, the interpretation is that the centrifugal force is an outgrowth of using polar coordinates. As Hildebrand says: "Since such quantities are not true physical forces, they are often called inertia forces. Their presence or absence depends, not upon the particular problem at hand, but upon the coordinate system chosen." In particular, if Cartesian coordinates are chosen, the centrifugal force disappears, and the formulation involves only the central force itself, which provides the centripetal force
Centripetal force
Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...
for a curved motion.
This viewpoint, that fictitious forces originate in the choice of coordinates, often is expressed by users of the Lagrangian method. This view arises naturally in the Lagrangian approach, because the frame of reference is (possibly unconsciously) selected by the choice of coordinates. Unfortunately, this usage of "inertial force" conflicts with the Newtonian idea of an inertial force. In the Newtonian view, an inertial force originates in the acceleration of the frame of observation (the fact that it is not an inertial frame of reference
Inertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
), not in the choice of coordinate system. To keep matters clear, it is safest to refer to the Lagrangian inertial forces as generalized inertial forces, to distinguish them from the Newtonian vector inertial forces. That is, one should avoid following Hildebrand when he says (p. 155) "we deal always with generalized forces, velocities accelerations, and momenta. For brevity, the adjective "generalized" frequently will be omitted."
It is known that the Lagrangian of a system is not unique. Within the Lagrangian formalism the Newtonian fictitious forces can be identified by the existence of alternative Lagrangians in which the fictitious forces disappear, sometimes found by exploiting the symmetry of the system.
Hamilton's principle
The action, denoted by, is the time integral of the Lagrangian:Let q0 and q1 be the coordinates at respective initial and final times t0 and t1. Using the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
, it can be shown the Lagrange's equations are equivalent to Hamilton's principle
Hamilton's principle
In physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action...
:
- The system undergoes the trajectory between t0 and t1 whose action has a stationary value.
By stationary, we mean that the action does not vary to first-order for infinitesimal deformations of the trajectory, with the end-points (q0, t0) and (q1,t1) fixed. Hamilton's principle can be written as:
Thus, instead of thinking about particles accelerating in response to applied forces, one might think of them picking out the path with a stationary action.
Hamilton's principle is sometimes referred to as the principle of least action
Principle of least action
In physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
. However, this is a misnomer: the action only needs to be stationary, with any variation h of the functional giving an increase in the functional integral of the action. This is not, as is frequently misstated, required to be a maximum or a minimum of the action functional.
We can use this principle instead of Newton's Laws as the fundamental principle of mechanics, this allows us to use an integral principle (Newton's Laws are based on differential equations so they are a differential principle) as the basis for mechanics. However it is not widely stated that Hamilton's principle is a variational principle only with holonomic
Holonomic
In mathematics and physics, the term holonomic may occur with several different meanings.-Holonomic basis:A holonomic basis for a manifold is a set of basis vectors ek for which all Lie derivatives vanish:[e_j,e_k]=0 \,...
constraints, if we are dealing with nonholonomic systems then the variational principle should be replaced with one involving d'Alembert principle of virtual work
Virtual work
Virtual work arises in the application of the principle of least action to the study of forces and movement of a mechanical system. Historically, virtual work and the associated calculus of variations were formulated to analyze systems of rigid bodies, but they have also been developed for the...
. Working only with holonomic constraints is the price we have to pay for using an elegant variational formulation of mechanics.
Extensions of Lagrangian mechanics
The HamiltonianHamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, denoted by H, is obtained by performing a Legendre transformation
Legendre transformation
In mathematics, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre, is an operation that transforms one real-valued function of a real variable into another...
on the Lagrangian, which introduces new variables, canonically conjugate to the original variables. This doubles the number of variables, but makes differential equations first order. The Hamiltonian is the basis for an alternative formulation of classical mechanics known as Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
. It is a particularly ubiquitous quantity in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
(see Hamiltonian (quantum mechanics)
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
).
In 1948, Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
discovered the path integral formulation
Path integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
extending the principle of least action
Principle of least action
In physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
to quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
for electrons and photons. In this formulation, particles travel every possible path between the initial and final states; the probability of a specific final state is obtained by summing over all possible trajectories leading to it. In the classical regime, the path integral formulation cleanly reproduces Hamilton's principle, and Fermat's principle
Fermat's principle
In optics, Fermat's principle or the principle of least time is the principle that the path taken between two points by a ray of light is the path that can be traversed in the least time. This principle is sometimes taken as the definition of a ray of light...
in optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
.
See also
- Canonical coordinatesCanonical coordinatesIn mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
- Functional derivativeFunctional derivativeIn mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
- Generalized coordinatesGeneralized coordinatesIn the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
- Hamiltonian mechanicsHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
- Lagrangian analysisLagrangian analysisLagrangian analysis is the use of Lagrangian coordinates to analyze various problems in continuum mechanics.Lagrangian analysis may be used to analyze currents and flows of various materials by analyzing data collected from gauges/sensors embedded in the material which freely move with the motion...
(applications of Lagrangian mechanics) - Restricted three-body problem
- Lagrangian PointLagrangian pointThe Lagrangian points are the five positions in an orbital configuration where a small object affected only by gravity can theoretically be stationary relative to two larger objects...
- Hamiltonian opticsHamiltonian opticsLagrangian optics and Hamiltonian optics are two formulations of geometrical optics which share much of the mathematical formalism with Lagrangian mechanics and Hamiltonian mechanics.-Hamilton's principle:...
Further reading
- Landau, L.D.Lev LandauLev Davidovich Landau was a prominent Soviet physicist who made fundamental contributions to many areas of theoretical physics...
and Lifshitz, E.M.Evgeny LifshitzEvgeny Mikhailovich Lifshitz was a leading Soviet physicist of Jewish origin and the brother of physicist Ilya Mikhailovich Lifshitz. Lifshitz is well known in general relativity for coauthoring the BKL conjecture concerning the nature of a generic curvature...
Mechanics, Pergamon Press. - Gupta, Kiran Chandra, Classical mechanics of particles and rigid bodies (Wiley, 1988).
External links
- Tong, David, Classical Dynamics Cambridge lecture notes
- Principle of least action interactive Excellent interactive explanation/webpage
- Aerospace dynamics lecture notes on Lagrangian mechanics
- Aerospace dynamics lecture notes on Rayleigh dissipation function
- Introduction to Lagrangian Mechanics
- Sydney Grammar School Academic Extension notes