Legendre transformation - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the Legendre transformation or Legendre transform, named after Adrien-Marie Legendre

Adrien-Marie Legendre

Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...

, is an operation that transforms one real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

-valued function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

of a real variable into another. Specifically, the Legendre transform of a convex function

Convex function

In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...

ƒ is the function ƒ^∗ defined by

If ƒ is differentiable, then ƒ^∗(p) can be interpreted as the negative of the y-intercept

Y-intercept

In coordinate geometry, using the common convention that the horizontal axis represents a variable x and the vertical axis represents a variable y, a y-intercept is a point where the graph of a function or relation intersects with the y-axis of the coordinate system...

of the tangent line to the graph

Graph of a function

In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...

of ƒ that has slope p. In particular, the value of x that attains the maximum has the property that

That is, the derivative of the function ƒ becomes the argument to the function ƒ^∗. In particular, if ƒ is convex

Convex function

(or concave up), then ƒ^∗ satisfies the functional equation

Functional equation

In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...

The Legendre transform is its own inverse. Like the familiar Fourier transform

Fourier transform

In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...

, the Legendre transform takes a function ƒ(x) and produces a function of a different variable p. However, while the Fourier transform consists of an integration with a kernel, the Legendre transform uses maximization as the transformation procedure. The transform is especially well behaved if ƒ(x) is a convex function.

The Legendre transformation is an application of the duality

Duality (projective geometry)

A striking feature of projective planes is the "symmetry" of the roles played by points and lines in the definitions and theorems, and duality is the formalization of this metamathematical concept. There are two approaches to the subject of duality, one through language and the other a more...

relationship between points and lines. The functional relationship specified by f(x) can be represented equally well as a set of (x, y) points, or as a set of tangent lines specified by their slope and intercept values.

The Legendre transformation can be generalized to the Legendre-Fenchel transformation. It is commonly used in thermodynamics

Thermodynamics

Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...

and in the Hamiltonian

Hamiltonian mechanics

Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...

formulation of classical mechanics.

Definitions

The definition of the Legendre transform can be made more explicit. To extremise

with respect to

, we set its derivative equal to zero:

Thus, the expression is extremised when

When

is convex

Convex function

, this is a maximum because the second derivative is negative:

Next we invert (2) to obtain

as a function of

and plug this into (1), which gives the more useful form,

This definition gives the conventional procedure for calculating the Legendre transform of

: find

, solve for

in terms of

and substitute into the expression

. This definition makes clear the following interpretation: the Legendre transform produces a new function, in which the independent variable

is replaced by

, which is the derivative of the original function with respect to

Another definition

There is a third definition of the Legendre transform:

and

are said to be Legendre transforms of each other if their first derivative

Derivative

In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...

s are inverse function

Inverse function

In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...

s of each other:

We can see this first by taking derivative of

Then this equation taken together with the previous equation resulting from the maximization condition results in the following pair of reciprocal equations:

From these we see that

and

are inverses, as promised. They are unique up to an additive constant which is fixed by the additional requirement that

Although in some cases (e.g. thermodynamic potentials) a non-standard requirement is used:

The standard constraint will be considered in this article unless otherwise noted. The Legendre transformation is its own inverse, and is related to integration by parts

Integration by parts

In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...

Thermodynamics

The strategy behind the use of Legendre transforms is to shift, from a function with one of its parameters an independent variable, to a new function with its dependence on a new variable (the partial derivative of the original function with respect to the independent variable). The new function is the difference between the original function and the product of the old and new variables. For example, while the internal energy

Internal energy

In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...

is an explicit function of the extensive variables entropy

Entropy

Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...

, volume

Volume

Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....

(and chemical composition)

the enthalpy

Enthalpy

Enthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...

, the (non standard) Legendre transform of U with respect to −PV

becomes a function of the entropy and the intensive quantity, pressure

Pressure

Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...

, as natural variables, and is useful when the (external) P is constant. The free energies

Thermodynamic free energy

The thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...

(Helmholtz and Gibbs), are obtained through further Legendre transforms, by subtracting TS (from U and H respectively), shift dependence from the entropy S to its conjugate intensive variable temperature

Thermodynamic temperature

Thermodynamic temperature is the absolute measure of temperature and is one of the principal parameters of thermodynamics. Thermodynamic temperature is an "absolute" scale because it is the measure of the fundamental property underlying temperature: its null or zero point, absolute zero, is the...

T, and are useful when it is constant.

Hamilton-Lagrange mechanics

A Legendre transform is used in classical mechanics

Classical mechanics

In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...

to derive the Hamiltonian formulation

Hamiltonian mechanics

from the Lagrangian one

Lagrangian mechanics

Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....

, and conversely. While the Lagrangian

Lagrangian

The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...

is an explicit function of the positional coordinates

Coordinate system

In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...

q_j and generalized velocities

Velocity

In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...

dq_j /dt (and time), the Hamiltonian shifts the functional dependence to the positions and momenta

Momentum

In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...

, defined as

.
Whenever

(in that case the Lagrangian is said to be regular) one can express the

as functions

and define

Each of the two formulations has its own applicability, both in the theoretical

Theory

The English word theory was derived from a technical term in Ancient Greek philosophy. The word theoria, , meant "a looking at, viewing, beholding", and referring to contemplation or speculation, as opposed to action...

foundations of the subject, and in practice, depending on the ease of calculation

Calculation

A calculation is a deliberate process for transforming one or more inputs into one or more results, with variable change.The term is used in a variety of senses, from the very definite arithmetical calculation of using an algorithm to the vague heuristics of calculating a strategy in a competition...

for a particular problem. The coordinates are not necessarily Cartesian

Cartesian coordinate system

A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...

, but can also be angle

Angle

In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...

s, etc. An optimum choice takes advantage of the actual physical symmetries

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

An example – variable capacitor

As another example from physics

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

, consider a parallel-plate capacitor

Capacitor

A capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...

in which the plates can move relative to one another. Such a capacitor would allow us to transfer the electric energy which is stored on the capacitor into external mechanical work done by the force

Force

In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...

s acting on the plates. You can think of the electric charge as analogous to the "charge" of a gas

Gas

Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...

in a cylinder

Cylinder (engine)

A cylinder is the central working part of a reciprocating engine or pump, the space in which a piston travels. Multiple cylinders are commonly arranged side by side in a bank, or engine block, which is typically cast from aluminum or cast iron before receiving precision machine work...

, and the resulting mechanical force

Force

being exerted on a piston

Piston

A piston is a component of reciprocating engines, reciprocating pumps, gas compressors and pneumatic cylinders, among other similar mechanisms. It is the moving component that is contained by a cylinder and is made gas-tight by piston rings. In an engine, its purpose is to transfer force from...

.

Suppose we wanted to compute the force on the plates as a function of x, the distance which separates them. To find the force we will compute the potential energy and then use the definition of force as the gradient of the potential energy function.

The energy stored in a capacitor of capacitance

Capacitance

In electromagnetism and electronics, capacitance is the ability of a capacitor to store energy in an electric field. Capacitance is also a measure of the amount of electric potential energy stored for a given electric potential. A common form of energy storage device is a parallel-plate capacitor...

C(x) and charge Q is

where we have abstracted away the dependence on the area of the plates, the dielectric constant of the material between the plates, and the separation x as the capacitance

Capacitance

C(x).

The force F between the plates due to the electric field is

If the capacitor is not connected to any circuit, then the charges

Electric charge

Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...

on the plates remain constant as they move, the force is the negative gradient

Gradient

In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....

of the electrostatic

Electrostatics

Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....

energy

However, if the volt

Volt

The volt is the SI derived unit for electric potential, electric potential difference, and electromotive force. The volt is named in honor of the Italian physicist Alessandro Volta , who invented the voltaic pile, possibly the first chemical battery.- Definition :A single volt is defined as the...

age between the plates V is maintained constant by connection to a battery

Battery (electricity)

An electrical battery is one or more electrochemical cells that convert stored chemical energy into electrical energy. Since the invention of the first battery in 1800 by Alessandro Volta and especially since the technically improved Daniell cell in 1836, batteries have become a common power...

, which is a reservoir for charge at constant potential difference.
To find the force we first compute the non-standard Legendre transform

The force now becomes the negative gradient of the Legendre transform

The two functions happen to be negatives only because of the linear

Linear

In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...

ity of the capacitance

Capacitance

Examples

The exponential function

Exponential function

In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...

e^x has x ln x − x as a Legendre transform since their respective first derivatives e^x and ln x are inverse to each other. This example shows that the respective domain

Domain (mathematics)

In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...

s of a function and its Legendre transform need not agree.

Similarly, the quadratic form

Quadratic form

In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....

with A a symmetric invertible n-by-n-matrix

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

has

as a Legendre transform.

Legendre transformation in one dimension

In one dimension, a Legendre transform to a function f : R → R with an invertible first derivative may be found using the formula

This can be seen by integrating both sides of the defining condition restricted to one-dimension

from x₀ to x₁, making use of the fundamental theorem of calculus

Fundamental theorem of calculus

The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...

on the left hand side and substituting

on the right hand side to find

with f*′(y₀) = x₀, f*′(y₁) = x₁. Using integration by parts

Integration by parts

In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...

the last integral simplifies to

Therefore,

Since the left hand side of this equation does only depend on x₁ and the right hand side only on x₀, they have to evaluate to the same constant.

Solving for f* and choosing C to be zero results in the above-mentioned formula.

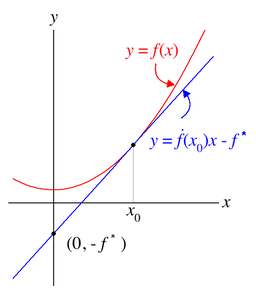
Geometric interpretation

For a strictly convex function the Legendre-transformation can be interpreted as a mapping between the graph

Graph of a function

of the function and the family of tangent

Tangent

In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...

s of the graph. (For a function of one variable, the tangents are well-defined at all but at most countably many

Countable set

In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...

points since a convex function is differentiable

Derivative

at all but at most countably many points.)

The equation of a line with slope

Slope

In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....

m and y-intercept

Y-intercept

b is given by

For this line to be tangent to the graph of a function f at the point (x₀, f(x₀)) requires

and

f is strictly monotone as the derivative of a strictly convex function, and the second equation can be solved for x₀, allowing to eliminate x₀ from the first giving the y-intercept b of the tangent as a function of its slope m:

Here f* denotes the Legendre transform of f.

The family

Indexed family

In mathematics, an indexed family is a collection of values that are associated with indexes. For example, a family of real numbers, indexed by the integers is a collection of real numbers, where each integer is associated with one of the real numbers....

of tangents of the graph of f parameterized by m is therefore given by

or, written implicitly, by the solutions of the equation

The graph of the original function can be reconstructed from this family of lines as the envelope

Envelope (mathematics)

In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...

of this family by demanding

Eliminating m from these two equations gives

Identifying y with f(x) and recognizing the right side of the preceding equation as the Legendre transform of f* we find

Legendre transformation in more than one dimension

For a differentiable real-valued function on an open

Open set

The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...

subset U of Rⁿ the Legendre conjugate of the pair (U, f) is defined to be the pair (V, g), where V is the image of U under the gradient

Gradient

mapping Df, and g is the function on V given by the formula

where

is the scalar product on Rⁿ. The multidimensional transform can be interpreted as an encoding of the convex hull

Convex hull

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

of the function's epigraph

Epigraph (mathematics)

In mathematics, the epigraph of a function f : Rn→R is the set of points lying on or above its graph:and the strict epigraph of the function is:The set is empty if f \equiv \infty ....

in terms of its supporting hyperplane

Supporting hyperplane

Supporting hyperplane is a concept in geometry. A hyperplane divides a space into two half-spaces. A hyperplane is said to support a set S in Euclidean space \mathbb R^n if it meets both of the following:...

s.http://maze5.net/?page_id=733

Alternatively, if X is a real vector space and Y is its dual vector space

Dual space

In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...

, then for each point x of X and y of Y, there is a natural identification of the cotangent space

Cotangent space

In differential geometry, one can attach to every point x of a smooth manifold a vector space called the cotangent space at x. Typically, the cotangent space is defined as the dual space of the tangent space at x, although there are more direct definitions...

s T*X_x with Y and T*Y_y with X. If f is a real differentiable function over X, then ∇f is a section of the cotangent bundle

Cotangent bundle

In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...

T*X and as such, we can construct a map from X to Y. Similarly, if g is a real differentiable function over Y, ∇g defines a map from Y to X. If both maps happen to be inverses of each other, we say we have a Legendre transform.

Further properties

In the following the Legendre transform of a function f is denoted as f*.

Scaling properties

The Legendre transformation has the following scaling properties: For a>0,

It follows that if a function is homogeneous of degree r

Homogeneous function

In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...

then its image under the Legendre transformation is a homogeneous function of degree s, where 1/r + 1/s = 1. Thus, the only monomial whose degree is invariant under Legendre transform is the quadratic.

Behavior under translation

Behavior under inversion

Behavior under linear transformations

Let A be a linear transformation

Linear transformation

In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...

from Rⁿ to R^m. For any convex function f on Rⁿ, one has