Duality (projective geometry)
Encyclopedia
A striking feature of projective planes
is the "symmetry
" of the roles played by points and lines in the definitions and theorems, and (plane) duality is the formalization of this metamathematical
concept. There are two approaches to the subject of duality, one through language (the Principle of Duality) and the other a more functional approach. These are completely equivalent and either treatment has as its starting point the axiomatic
version of the geometries under consideration. In the functional approach there is a map between related geometries which is called a duality. In specific examples, such a map can be constructed in many ways. The concept of plane duality readily extends to space duality and beyond that to duality in any finite dimensional projective geometry.
axiomatically as an incidence structure
, in terms of a set P of points, a set L of lines, and an incidence relation I that determines which points lie on which lines, then one may define a plane dual structure.
Interchange the role of "points" and "lines" in
to obtain the dual structure
where I* is the inverse relation
of I. C* is also a projective plane, called the dual plane of C.
If C and C* are isomorphic, then C is called self-dual. The projective planes PG(2,K) for any division ring K are self-dual. However, there are non-Desarguesian planes
which are not self-dual, such as the Hall planes and some that are, such as the Hughes planes
.
In a projective plane a statement involving points, lines and incidence between them that is obtained from another such statement by interchanging the words "point" and "line" and making whatever grammatical adjustments that are necessary, is called the plane dual statement of the first. The plane dual statement of "Two points are on a unique line." is "Two lines meet at a unique point." Forming the plane dual of a statement is known as dualizing the statement.
If a statement is true in a projective plane C, then the plane dual of that statement must be true in the dual plane C*. This follows since dualizing each statement in the proof "in C" gives a statement of the proof "in C*."
The Principle of Plane Duality says that dualizing any theorem in a self-dual projective plane C produces another theorem valid in C.
The above concepts can be generalized to talk about space duality, where the terms "points" and "planes" are interchanged (and lines remain lines). This leads to the Principle of Space Duality. Further generalization is possible (see below).
These principles provide a good reason for preferring to use a "symmetric" term for the incidence relation. Thus instead of saying "a point lies on a line" one should say "a point is incident with a line" since dualizing the latter only involves interchanging point and line ("a line is incident with a point").
In the special case that the projective plane is of the PG(2,K)
type, with K a division ring, a duality is called a reciprocity. These planes are always self-dual. By the Fundamental theorem of projective geometry a reciprocity is the composition of an automorphic function
of K and a homography
. If the automorphism involved is the identity, then the reciprocity is called a projective correlation.
A correlation of order two (an involution) is called a polarity. If a correlation φ is not a polarity then φ2 is a nontrivial collineation.
This duality mapping concept can also be extended to higher dimensional spaces so the modifier "(plane)" can be dropped in those situations.
s, transformations of PG(n,K) (also denoted by KPn) with K a field, that interchange objects of dimension r with objects of dimension n - 1 - r ( = codimension
r + 1). That is, in a projective space of dimension n, the points (dimension 0) are made to correspond with hyperplane
s (codimension 1), the lines joining two points (dimension 1) are made to correspond with the intersection of two hyperplanes (codimension 2), and so on.
The points of PG(n,K) can be taken to be the nonzero vectors in the (n + 1)-dimensional vector space over K, where we identify two vectors which differ by a scalar factor. Another way to put it is that the points of n-dimensional projective space are the lines through the origin in Kn + 1, which are 1-dimensional vector subspaces
. Also the n- vector dimensional subspaces of Kn + 1 represent the (n − 1)- geometric dimensional hyperplanes of projective n-space over K.
A nonzero vector u = (u0,u1,...,un) in Kn + 1 also determines an (n - 1) - geometric dimensional subspace (hyperplane) Hu, by
When a vector u is used to define a hyperplane in this way it shall be denoted by uH, while if it is designating a point we will use uP. In terms of the usual dot product
, Hu = {xP : uH • xP = 0}. Since K is a field, the dot product is symmetrical, meaning uH•xP = u0x0 + u1x1 + ... + unxn = x0u0 + x1u1 + ... + xnun = xH•uP. A reciprocity can be given by uP ↔ Hu between points and hyperplanes. This extends to a reciprocity between the line generated by two points and the intersection of two such hyperplanes, and so forth.
In the projective plane, PG(2,K), with K a field we have the reciprocity given by: points in homogeneous coordinates
(a,b,c) ↔ lines with equations ax + by + cz = 0. In a corresponding projective space, PG(3,K), a reciprocity is given by: points in homogeneous coordinates (a,b,c,d) ↔ planes with equations ax + by + cz + dw = 0. This reciprocity would also map a line determined by two points (a1,b1,c1,d1) and (a2,b2,c2,d2) to the line which is the intersection of the two planes with equations a1x + b1y + c1z + d1w = 0 and a2x + b2y + c2z + d2w = 0.
in solid geometry
is obtained, where points are dual to faces, and sides are dual to sides, so that the icosahedron
is dual to the dodecahedron, and the cube
is dual to the octahedron
.
of the real projective plane
which is a "unit sphere with antipodes identified", or equivalently, the model of lines and planes through the origin of the vector space K3. Associate a line through the origin with the unique plane through the origin which is perpendicular (orthogonal) to the line. When, in the model, these lines are considered to be the points and the planes the lines of the projective plane PG(2,K), this association becomes a reciprocity (actually a polarity) of the projective plane. The sphere model is obtained by intersecting the lines and planes through the origin with a unit sphere centered at the origin. The lines meet the sphere in antipodal points which must then be identified to obtain a point of the projective plane, and the planes meet the sphere in great circles
which are thus the lines of the projective plane.
That this association "preserves" incidence is most easily seen from the lines and planes model. A point incident with a line in the projective plane corresponds to a line lying in a plane in the model. Applying the association, the plane becomes a line through the origin perpendicular to the plane it is associated with. This image line is perpendicular to every line of the plane which passes through the origin, in particular the original line (point of the projective plane). All lines that are perpendicular to the original line at the origin lie in the unique plane which is orthogonal to the original line, that is, the image plane under the association. Thus, the image line lies in the image plane and the association preserves incidence.
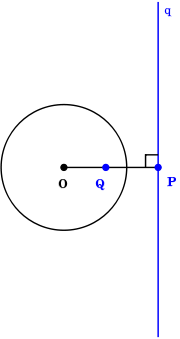In the Euclidean plane, fix a circle C with center O and radius r. For each point P other than O define an image point P so that OP • OP' = r2. The mapping defined by P → P' is called inversion with respect to circle C. The line through P' which is perpendicular to the line OP is called the polar of the point P with respect to circle C. Let m be a line not passing through O. Drop a perpendicular from O to m, meeting m at the point Q (this is the point of m that is closest to O). The image of Q under inversion with respect to C is called the pole of m. If a point P (different from O) is on a line m (not passing through O) then the pole of m lies on the polar of P and viceversa. The incidence preserving process, in which points and lines are transformed into their polars and poles with respect to C is called reciprocation. In order to turn this process into a reciprocity, the Euclidean plane (which is not a projective plane) needs to be expanded to the extended euclidean plane
by adding a line at infinity
and points at infinity which lie on this line. In this expanded plane, we define the polar of the point O to be the line at infinity (and O is the pole of the line at infinity), and the poles of the lines through O are the points of infinity where, if a line has slope
s (≠ 0) its pole is the infinite point associated to the parallel class of lines with slope -1/s. The pole of the x-axis is the point of infinity of the vertical lines and the pole of the y-axis is the point of infinity of the horizontal lines.
The construction of a reciprocity based on inversion in a circle given above can be generalized by using inversion in a conic section (in the extended real plane). The reciprocities constructed in this manner are projective correlations of order two, that is, polarities.
(w.r.t. incidence properties) to the planar model: the affine plane extended with a projective line at infinity.
To map a point on the sphere to a point on the plane, let the plane be tangent to the sphere at some point which shall be the origin of the plane's coordinate system (2-D origin). Then construct a line passing through the center of the sphere (3-D origin) and the point on the sphere. This line intersects the plane at a point which is the projection of the point on the sphere onto the plane (or vice versa).
This projection can be used to define a one-to-one onto mapping
If points in
are expressed in homogeneous coordinates
, then
Also, lines in the planar model are projections of great circles of the sphere. This is so because through any line in the plane pass an infinitude of different planes: one of these planes passes through the 3-D origin, but a plane passing through the 3-D origin intersects the sphere along a great circle.
As we have seen, any great circle in the unit sphere has a projective point perpendicular to it, which can be defined as its dual. But this point is a pair of antipodal points on the unit sphere, through both of which passes a unique 3-D line, and this line extended past the unit sphere intersects the tangent plane at a point, which means that there is a geometric way to associate a unique point on the plane to every line on the plane, such that the point is the dual of the line.
of the distance of line L to the origin.
Expressed algebraically, let g be a one-to-one mapping from the projective plane onto itself:
such that
and
where the L subscript is used to semantically distinguish line coordinates
from point coordinates. In words, affine line (m, b) with slope m and y-intercept b is the dual of point (m/b, −1/b). If b=0 then the line passes through the 2-D origin and its dual is the ideal point [m : −1 : 0].
The affine point with Cartesian coordinates (x,y) has as its dual the line whose slope is −x/y and whose y-intercept is −1/y. If the point is the 2-D origin [0:0:1], then its dual is [0:1:0]L which is the line at infinity. If the point is [x:0:1], on the x-axis, then its dual is line [x:1:0]L which shall be interpreted as a line whose slope is vertical and whose x-intercept is −1/x.
If a point or a line's homogeneous coordinates are represented as a vector in 3x1 matrix
form, then the duality mapping g can be represented by a 3x3 matrix
whose inverse is
Matrix G has one real eigenvalue: one, whose eigenvector is [1:0:0]. The line [1:0:0]L is the y-axis, whose dual is the ideal point [1:0:0] which is the intersection of the ideal line with the x-axis.
Notice that [1:0:0]L is the y-axis, [0:1:0]L is the line at infinity, and [0:0:1]L is the x-axis. In 3-space, matrix G is a 90° rotation about the x-axis which turns the y-axis into the z-axis. In projective 2-space, matrix G is a projective transformation which maps points to points, lines to lines, conic sections to conic sections: it exchanges the line at infinity with the x-axis and maps the y-axis onto itself through a Möbius transformation. As a duality, matrix G pairs up each projective line with its dual projective point.
.
Given points P1 and P2 through which passes line L, P1.P2 = L, then what is the intersection of lines g−1P1 and g−1P2? If g−1P1 ∩ g−1P2 = P then
so that
Given a pair of affine points in homogeneous coordinates, the line passing through them is
where the cross product
is computed just as it would for an ordinary pair vectors in 3-space.
From this last equation can be derived the intersection of lines, by using the mapping g to "plug in" the lines into the slots for points:
where mapping g is seen to distribute with respect to the cross product: i.e. g is an isomorphism of cross product.
Theorem. The duality mapping g is an isomorphism of cross product. I.e. g is distributive w.r.t. cross product.
Proof. Given points A=(a:b:c) and B=(d:e:f), their cross product is
but
Therefore
.
Q.E.D.
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
is the "symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
" of the roles played by points and lines in the definitions and theorems, and (plane) duality is the formalization of this metamathematical
Metamathematics
Metamathematics is the study of mathematics itself using mathematical methods. This study produces metatheories, which are mathematical theories about other mathematical theories...
concept. There are two approaches to the subject of duality, one through language (the Principle of Duality) and the other a more functional approach. These are completely equivalent and either treatment has as its starting point the axiomatic
Axiomatic
* In mathematics, an "axiomatic" theory is one based on axioms* Axiomatic , a collection of short stories by Greg Egan* Axiomatic , a 2005 album by Australian band Taxiride...
version of the geometries under consideration. In the functional approach there is a map between related geometries which is called a duality. In specific examples, such a map can be constructed in many ways. The concept of plane duality readily extends to space duality and beyond that to duality in any finite dimensional projective geometry.
Principle of Duality
If one defines a projective planeProjective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
axiomatically as an incidence structure
Incidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
, in terms of a set P of points, a set L of lines, and an incidence relation I that determines which points lie on which lines, then one may define a plane dual structure.
Interchange the role of "points" and "lines" in
- C=(P,L,I)
to obtain the dual structure
- C* =(L,P,I*),
where I* is the inverse relation
Inverse relation
In mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...
of I. C* is also a projective plane, called the dual plane of C.
If C and C* are isomorphic, then C is called self-dual. The projective planes PG(2,K) for any division ring K are self-dual. However, there are non-Desarguesian planes
Non-Desarguesian plane
In mathematics, a non-Desarguesian plane, named after Gérard Desargues, is a projective plane that does not satisfy Desargues's theorem, or in other words a plane that is not a Desarguesian plane...
which are not self-dual, such as the Hall planes and some that are, such as the Hughes planes
Hughes plane
In mathematics, a Hughes plane is one of the non-Desarguesian projective planes found by .There are examples of order p2n for every odd prime p and every positive integer n....
.
In a projective plane a statement involving points, lines and incidence between them that is obtained from another such statement by interchanging the words "point" and "line" and making whatever grammatical adjustments that are necessary, is called the plane dual statement of the first. The plane dual statement of "Two points are on a unique line." is "Two lines meet at a unique point." Forming the plane dual of a statement is known as dualizing the statement.
If a statement is true in a projective plane C, then the plane dual of that statement must be true in the dual plane C*. This follows since dualizing each statement in the proof "in C" gives a statement of the proof "in C*."
The Principle of Plane Duality says that dualizing any theorem in a self-dual projective plane C produces another theorem valid in C.
The above concepts can be generalized to talk about space duality, where the terms "points" and "planes" are interchanged (and lines remain lines). This leads to the Principle of Space Duality. Further generalization is possible (see below).
These principles provide a good reason for preferring to use a "symmetric" term for the incidence relation. Thus instead of saying "a point lies on a line" one should say "a point is incident with a line" since dualizing the latter only involves interchanging point and line ("a line is incident with a point").
Dual Theorems
As the real projective plane, PG(2,R), is self-dual there are a number of pairs of well known results that are duals of each other. Some of these are:- Desargues' theoremDesargues' theoremIn projective geometry, Desargues' theorem, named in honor of Gérard Desargues, states:Denote the three vertices of one triangle by a, b, and c, and those of the other by A, B, and C...
⇔ Converse of Desargues' theoremDesargues' theoremIn projective geometry, Desargues' theorem, named in honor of Gérard Desargues, states:Denote the three vertices of one triangle by a, b, and c, and those of the other by A, B, and C...
- Pascal's theoremPascal's theoremIn projective geometry, Pascal's theorem states that if an arbitrary hexagon is inscribed in any conic section, and pairs of opposite sides are extended until they meet, the three intersection points will lie on a straight line, the Pascal line of that configuration.- Related results :This theorem...
⇔ Brianchon's theoremBrianchon's theoremIn geometry, Brianchon's theorem, named after Charles Julien Brianchon , is as follows. Let ABCDEF be a hexagon formed by six tangent lines of a conic section...
- Menelaus' theoremMenelaus' theoremMenelaus' theorem, named for Menelaus of Alexandria, is a theorem about triangles in plane geometry. Given a triangle ABC, and a transversal line that crosses BC, AC and AB at points D, E and F respectively, with D, E, and F distinct from A, B and C, thenThis equation uses signed lengths of...
⇔ Ceva's theoremCeva's theoremCeva's theorem is a theorem about triangles in plane geometry. Given a triangle ABC, let the lines AO, BO and CO be drawn from the vertices to a common point O to meet opposite sides at D, E and F respectively...
Duality as a mapping
A (plane) duality is a map from a projective plane C = (P,L,I) to its dual plane C* = (L,P,I*) (see above) which preserves incidence. That is, a (plane) duality σ will map points to lines and lines to points (Pσ = L and Lσ = P) in such a way that if a point Q is on a line m ( denoted by Q I m) then Qσ I* mσ ⇔ mσ I Qσ. A (plane) duality which is an isomorphism is called a correlation. The existence of a correlation means that the projective plane C is self-dual.In the special case that the projective plane is of the PG(2,K)
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
type, with K a division ring, a duality is called a reciprocity. These planes are always self-dual. By the Fundamental theorem of projective geometry a reciprocity is the composition of an automorphic function
Automorphic function
In mathematics, an automorphic function is a function on a space that is invariant under the action of some group, in other words a function on the quotient space. Often the space is a complex manifold and the group is a discrete group....
of K and a homography
Homography
Homography is a concept in the mathematical science of geometry.A homography is an invertible transformation from a projective space to itself that maps straight lines to straight lines...
. If the automorphism involved is the identity, then the reciprocity is called a projective correlation.
A correlation of order two (an involution) is called a polarity. If a correlation φ is not a polarity then φ2 is a nontrivial collineation.
This duality mapping concept can also be extended to higher dimensional spaces so the modifier "(plane)" can be dropped in those situations.
Higher dimensional duality
Duality in the projective plane is a special case of duality for projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
s, transformations of PG(n,K) (also denoted by KPn) with K a field, that interchange objects of dimension r with objects of dimension n - 1 - r ( = codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
r + 1). That is, in a projective space of dimension n, the points (dimension 0) are made to correspond with hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
s (codimension 1), the lines joining two points (dimension 1) are made to correspond with the intersection of two hyperplanes (codimension 2), and so on.
The points of PG(n,K) can be taken to be the nonzero vectors in the (n + 1)-dimensional vector space over K, where we identify two vectors which differ by a scalar factor. Another way to put it is that the points of n-dimensional projective space are the lines through the origin in Kn + 1, which are 1-dimensional vector subspaces
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
. Also the n- vector dimensional subspaces of Kn + 1 represent the (n − 1)- geometric dimensional hyperplanes of projective n-space over K.
A nonzero vector u = (u0,u1,...,un) in Kn + 1 also determines an (n - 1) - geometric dimensional subspace (hyperplane) Hu, by
- Hu = {(
When a vector u is used to define a hyperplane in this way it shall be denoted by uH, while if it is designating a point we will use uP. In terms of the usual dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
, Hu = {xP : uH • xP = 0}. Since K is a field, the dot product is symmetrical, meaning uH•xP = u0x0 + u1x1 + ... + unxn = x0u0 + x1u1 + ... + xnun = xH•uP. A reciprocity can be given by uP ↔ Hu between points and hyperplanes. This extends to a reciprocity between the line generated by two points and the intersection of two such hyperplanes, and so forth.
In the projective plane, PG(2,K), with K a field we have the reciprocity given by: points in homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
(a,b,c) ↔ lines with equations ax + by + cz = 0. In a corresponding projective space, PG(3,K), a reciprocity is given by: points in homogeneous coordinates (a,b,c,d) ↔ planes with equations ax + by + cz + dw = 0. This reciprocity would also map a line determined by two points (a1,b1,c1,d1) and (a2,b2,c2,d2) to the line which is the intersection of the two planes with equations a1x + b1y + c1z + d1w = 0 and a2x + b2y + c2z + d2w = 0.
Three dimensions
In a polarity of real projective 3-space, PG(3,R), points correspond to planes, and lines correspond to lines. By restriction the duality of polyhedraDual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
in solid geometry
Solid geometry
In mathematics, solid geometry was the traditional name for the geometry of three-dimensional Euclidean space — for practical purposes the kind of space we live in. It was developed following the development of plane geometry...
is obtained, where points are dual to faces, and sides are dual to sides, so that the icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
is dual to the dodecahedron, and the cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
is dual to the octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
.
Geometric construction of a reciprocity
The reciprocity of PG(2,K), with K a field, given by homogeneous coordinates can also be described geometrically. This uses the modelMathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
of the real projective plane
Real projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
which is a "unit sphere with antipodes identified", or equivalently, the model of lines and planes through the origin of the vector space K3. Associate a line through the origin with the unique plane through the origin which is perpendicular (orthogonal) to the line. When, in the model, these lines are considered to be the points and the planes the lines of the projective plane PG(2,K), this association becomes a reciprocity (actually a polarity) of the projective plane. The sphere model is obtained by intersecting the lines and planes through the origin with a unit sphere centered at the origin. The lines meet the sphere in antipodal points which must then be identified to obtain a point of the projective plane, and the planes meet the sphere in great circles
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
which are thus the lines of the projective plane.
That this association "preserves" incidence is most easily seen from the lines and planes model. A point incident with a line in the projective plane corresponds to a line lying in a plane in the model. Applying the association, the plane becomes a line through the origin perpendicular to the plane it is associated with. This image line is perpendicular to every line of the plane which passes through the origin, in particular the original line (point of the projective plane). All lines that are perpendicular to the original line at the origin lie in the unique plane which is orthogonal to the original line, that is, the image plane under the association. Thus, the image line lies in the image plane and the association preserves incidence.
Poles and polars
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
by adding a line at infinity
Line at infinity
In geometry and topology, the line at infinity is a line that is added to the real plane in order to give closure to, and remove the exceptional cases from, the incidence properties of the resulting projective plane. The line at infinity is also called the ideal line.-Geometric formulation:In...
and points at infinity which lie on this line. In this expanded plane, we define the polar of the point O to be the line at infinity (and O is the pole of the line at infinity), and the poles of the lines through O are the points of infinity where, if a line has slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
s (≠ 0) its pole is the infinite point associated to the parallel class of lines with slope -1/s. The pole of the x-axis is the point of infinity of the vertical lines and the pole of the y-axis is the point of infinity of the horizontal lines.
The construction of a reciprocity based on inversion in a circle given above can be generalized by using inversion in a conic section (in the extended real plane). The reciprocities constructed in this manner are projective correlations of order two, that is, polarities.
Mapping the sphere onto the plane
The unit sphere modulo −1 model of the projective plane is isomorphicIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
(w.r.t. incidence properties) to the planar model: the affine plane extended with a projective line at infinity.
To map a point on the sphere to a point on the plane, let the plane be tangent to the sphere at some point which shall be the origin of the plane's coordinate system (2-D origin). Then construct a line passing through the center of the sphere (3-D origin) and the point on the sphere. This line intersects the plane at a point which is the projection of the point on the sphere onto the plane (or vice versa).
This projection can be used to define a one-to-one onto mapping
If points in
are expressed in homogeneous coordinatesHomogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
, then
Also, lines in the planar model are projections of great circles of the sphere. This is so because through any line in the plane pass an infinitude of different planes: one of these planes passes through the 3-D origin, but a plane passing through the 3-D origin intersects the sphere along a great circle.
As we have seen, any great circle in the unit sphere has a projective point perpendicular to it, which can be defined as its dual. But this point is a pair of antipodal points on the unit sphere, through both of which passes a unique 3-D line, and this line extended past the unit sphere intersects the tangent plane at a point, which means that there is a geometric way to associate a unique point on the plane to every line on the plane, such that the point is the dual of the line.
Duality mapping defined
Given a line L in the projective plane, what is its dual point? Draw a line L′ passing through the 2-D origin and perpendicular to line L. Then pick a point P on line L′ on the other side of the origin from line L, such that the distance of point P to the origin is the reciprocalMultiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
of the distance of line L to the origin.
-
- Figure 1. Three pairs of dual points and lines: one red pair, one yellow pair,
and one blue pair. The duality is an isomorphism of incidence, so that, e.g.,
the line passing through the red and yellow points is dual to the intersection
of the red and yellow lines.
Expressed algebraically, let g be a one-to-one mapping from the projective plane onto itself:
such that
and
where the L subscript is used to semantically distinguish line coordinates
Line coordinates
In geometry, line coordinates are used to specify the position of a line just as point coordinates are used to specify the position of a point.-Lines in the plane:...
from point coordinates. In words, affine line (m, b) with slope m and y-intercept b is the dual of point (m/b, −1/b). If b=0 then the line passes through the 2-D origin and its dual is the ideal point [m : −1 : 0].
The affine point with Cartesian coordinates (x,y) has as its dual the line whose slope is −x/y and whose y-intercept is −1/y. If the point is the 2-D origin [0:0:1], then its dual is [0:1:0]L which is the line at infinity. If the point is [x:0:1], on the x-axis, then its dual is line [x:1:0]L which shall be interpreted as a line whose slope is vertical and whose x-intercept is −1/x.
If a point or a line's homogeneous coordinates are represented as a vector in 3x1 matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
form, then the duality mapping g can be represented by a 3x3 matrix
whose inverse is
Matrix G has one real eigenvalue: one, whose eigenvector is [1:0:0]. The line [1:0:0]L is the y-axis, whose dual is the ideal point [1:0:0] which is the intersection of the ideal line with the x-axis.
Notice that [1:0:0]L is the y-axis, [0:1:0]L is the line at infinity, and [0:0:1]L is the x-axis. In 3-space, matrix G is a 90° rotation about the x-axis which turns the y-axis into the z-axis. In projective 2-space, matrix G is a projective transformation which maps points to points, lines to lines, conic sections to conic sections: it exchanges the line at infinity with the x-axis and maps the y-axis onto itself through a Möbius transformation. As a duality, matrix G pairs up each projective line with its dual projective point.
Preservation of incidence
The duality mapping g is an isomorphism with respect to the incidence properties (such as collinearity and concurrency). The mapping g has this property: given a pair of lines L1 and L2 which intersect at a point P, then their dual points gL1 and gL2 define the unique line g−1P:.Given points P1 and P2 through which passes line L, P1.P2 = L, then what is the intersection of lines g−1P1 and g−1P2? If g−1P1 ∩ g−1P2 = P then
so that
- ∴
Given a pair of affine points in homogeneous coordinates, the line passing through them is
where the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
is computed just as it would for an ordinary pair vectors in 3-space.
From this last equation can be derived the intersection of lines, by using the mapping g to "plug in" the lines into the slots for points:
where mapping g is seen to distribute with respect to the cross product: i.e. g is an isomorphism of cross product.
Theorem. The duality mapping g is an isomorphism of cross product. I.e. g is distributive w.r.t. cross product.
Proof. Given points A=(a:b:c) and B=(d:e:f), their cross product is
but
-
-
-
.
-
-
Therefore
.Q.E.D.
Q.E.D.
Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...