In
geometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
,
polyhedraIn elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
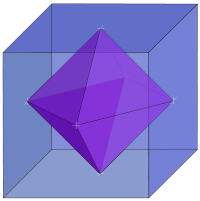
are associated into pairs called
duals, where the vertices of one correspond to the
faceIn geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
s of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another with equivalent edges. So the regular polyhedra — the
Platonic solidIn geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s and Kepler-Poinsot polyhedra — are arranged into dual pairs, with the exception of the regular
tetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
which is self-dual.
Duality is also sometimes called
reciprocity or
polarity.
Kinds of duality
There are many kinds of duality. The kinds most relevant to polyhedra are:
- Polar reciprocity
- Topological duality
- Abstract duality
Polar reciprocation
Duality is most commonly defined in terms of polar reciprocation about a concentric sphere. Here, each vertex (pole) is associated with a face plane (polar plane or just polar) so that the ray from the center to the vertex is perpendicular to the plane, and the product of the distances from the center to each is equal to the square of the radius. In coordinates, for reciprocation about the sphere
the vertex
is associated with the plane
.
The vertices of the dual, then, are the poles reciprocal to the face planes of the original, and the faces of the dual lie in the polars reciprocal to the vertices of the original. Also, any two adjacent vertices define an edge, and these will reciprocate to two adjacent faces which intersect to define an edge of the dual.
Notice that the exact form of the dual will depend on what sphere we reciprocate with respect to; as we move the sphere around, the dual form distorts. The choice of center (of the sphere) is sufficient to define the dual up to similarity. If multiple symmetry axes are present, they will necessarily intersect at a single point, and this is usually taken to be the center. Failing that a circumscribed sphere, inscribed sphere, or midsphere (one with all edges as tangents) can be used.
If a polyhedron has an element passing through the center of the sphere, the corresponding element of its dual will go to infinity. Since traditional "Euclidean" space never reaches infinity, the projective equivalent, called extended Euclidean space, must be formed by adding the required 'plane at infinity'. Some theorists prefer to stick to Euclidean space and say that there is no dual. Meanwhile Wenninger (1983) found a way to represent these infinite duals, in a manner suitable for making models (of some finite portion!).
The concept of
duality here is closely related to the
dualityA striking feature of projective planes is the "symmetry" of the roles played by points and lines in the definitions and theorems, and duality is the formalization of this metamathematical concept. There are two approaches to the subject of duality, one through language and the other a more...
in
projective geometryIn mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, where lines and edges are interchanged; in fact it is often mistakenly taken to be a particular version of the same. Projective polarity works well enough for convex polyhedra. But for non-convex figures such as star polyhedra, when we seek to rigorously define this form of polyhedral duality in terms of projective polarity, various problems appear. See for example Grünbaum & Shepherd (1988), and Gailiunas & Sharp (2005). Wenninger (1983) also discusses some issues on the way to deriving his infinite duals.
Canonical duals
Any convex polyhedron can be distorted into a canonical form, in which a
midsphereIn geometry, the midsphere or intersphere of a polyhedron is a sphere which is tangent to every edge of the polyhedron. That is to say, it touches any given edge at exactly one point...
(or intersphere) exists tangent to every edge, such that the average position of these points is the center of the sphere, and this form is unique up to congruences.
If we reciprocate such a polyhedron about its intersphere, the dual polyhedron will share the same edge-tangency points and so must also be canonical; it is the canonical dual, and the two together form a canonical dual compound.
Topological duality
We can distort a dual polyhedron such that it can no longer be obtained by reciprocating the original in any sphere; in this case we can say that the two polyhedra are still topologically dual.
It is worth noting that the vertices and edges of a convex polyhedron can be projected to form a
graphIn mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
(sometimes called a
Schlegel diagram) on the sphere or on a flat plane, and the corresponding graph formed by the dual of this polyhedron is its
dual graphIn mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
.
Abstract duality
An
abstract polyhedronIn mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...
is a certain kind of
partially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
(poset) of elements, such that adjacencies, or connections, between elements of the set correspond to adjacencies between elements (faces, edges, etc.) of a polyhedron. Such a poset may be represented in a
Hasse diagramIn order theory, a branch of mathematics, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction...
. Any such poset has a dual poset. The Hasse diagram of the dual polyhedron is obtained very simply, by turning the original diagram upside-down.
Dorman Luke construction
For a
uniform polyhedronA uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
, the face of the dual polyhedron may be found from the original polyhedron's
vertex figureIn geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
using the
Dorman Luke construction. This construction was originally described by Cundy & Rollett (1961) and later generalised by Wenninger (1983).
As an example, here is the vertex figure (red) of the
cuboctahedronIn geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...
being used to derive a face (blue) of the
rhombic dodecahedronIn geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...
.
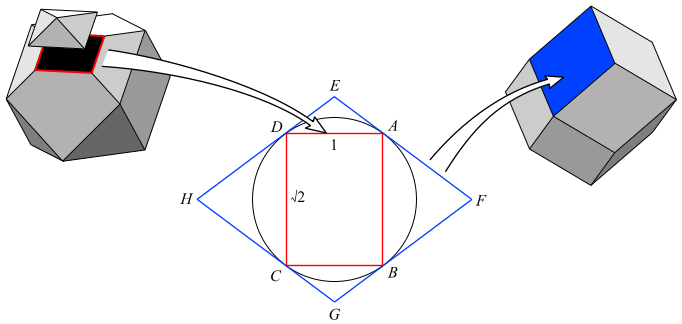
Before beginning the construction, the
vertex figureIn geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
ABCD is (in this case) obtained by cutting each connected edge at its mid-point.
Dorman Luke's construction then proceeds:
-
- Draw the circumcircle (tangent to every corner).
- Draw lines tangent to the circumcircle at each corner A, B, C, D.
- Mark the points E, F, G, H, where each line meets the adjacent line.
- The polygon EFGH is a face of the dual polyhedron.
The size of the vertex figure was chosen so that its circumcircle lies on the intersphere of the cuboctahedron, which also becomes the intersphere of the dual rhombic dodecahedron.
Dorman Luke's construction can only be used where a polyhedron has such an intersphere and the vertex figure is cyclic, i.e. for
uniform polyhedraA uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
.
Self-dual polyhedra
A
self-dual polyhedron is a
polyhedronIn elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
whose dual is a congruent figure, though not necessarily the identical figure: for example, the dual of a regular tetrahedron is a regular tetrahedron "facing the opposite direction" (reflected through the origin).
A self-dual polyhedron must have the same number of vertices as faces. We can distinguish between structural (
topologicalTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
) duality and
geometricalGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
duality. The topological structure of a self-dual polyhedron is also self-dual. Whether or not such a polyhedron is also geometrically self-dual will depend on the particular geometrical duality being considered. For example, every polygon is
topologically self-dual (it has the same number of vertices as edges, and these are switched by duality), but will not in general be
geometrically self-dual (up to rigid motion, for instance) – regular polygons are geometrically self-dual (all angles are congruent, as are all edges, so under duality these congruences swap), but irregular polygons may not be geometrically self-dual.
The most common geometric arrangement is where some convex polyhedron is in its canonical form, which is to say that the all its edges must be tangent to a certain sphere whose centre coincides with the centre of gravity (average position) of the tangent points. If the polar reciprocal of the canonical form in the sphere is congruent to the original, then the figure is self-dual.
There are infinitely many self-dual polyhedra. The simplest infinite family are the
pyramidsIn geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base....
of
n sides and of canonical form. Another infinite family consists of polyhedra that can be roughly described as a pyramid sitting on top of a
prismIn geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
(with the same number of sides). Add a frustum (pyramid with the top cut off) below the prism and you get another infinite family, and so on.
There are many other convex, self-dual polyhedra. For example, there are 6 different ones with 7 vertices, and 16 with 8 vertices.
Non-convex self-dual polyhedra can also be found, for example there is one among the
facettingIn geometry, facetting is the process of removing parts of a polygon, polyhedron or polytope, without creating any new vertices.Facetting is the reciprocal or dual process to stellation...
s of the regular
dodecahedron (and hence by duality also among the
stellationStellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
s of the
icosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
).
Family of pyramidsIn geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base....
TetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
|
Square pyramidIn geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it will have C4v symmetry.- Johnson solid :...
|
Pentagonal pyramidIn geometry, a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point . Like any pyramid, it is self-dual....
|
Hexagonal pyramidIn geometry, a hexagonal pyramid is a pyramid with a hexagonal base upon which are erected six triangular faces that meet at a point...
|
Family of elongated pyramids
Elongated triangular pyramidIn geometry, the elongated triangular pyramid is one of the Johnson solids . Norman Johnson discovered elongated triangular pyramids. As the name suggests, it can be constructed by elongating a tetrahedron by attaching a triangular prism to its base...
|
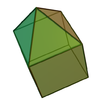Elongated square pyramidIn geometry, the elongated square pyramid is one of the Johnson solids . As the name suggests, it can be constructed by elongating a square pyramid by attaching a cube to its square base...
|
Elongated pentagonal pyramidIn geometry, the elongated pentagonal pyramid is one of the Johnson solids . As the name suggests, it can be constructed by elongating a pentagonal pyramid by attaching a pentagonal prism to its base....
|
Self dual compound polyhedra
The
Stella octangulaThe stellated octahedron, or stella octangula, is the only stellation of the octahedron. It was named by Johannes Kepler in 1609, though it was known to earlier geometers...
, being a compound of two
tetrahedraIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
is also self-dual, as well as four other regular-dual compounds.
Dual polytopes and tessellations
Duality can be generalized to
n-dimensional space and
dual polytopeIn elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
s; in 2-dimensions these are called
dual polygonIn geometry, polygons are associated into pairs called duals, where the vertices of one correspond to the edges of the other.-Properties:Regular polygons are self-dual....
s.
The vertices of one polytope correspond to the (
n − 1)-dimensional elements, or facets, of the other, and the
j points that define a (
j − 1)-dimensional element will correspond to
j hyperplanes that intersect to give a (
n −
j)-dimensional element. The dual of a
honeycombIn geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
can be defined similarly.
In general, the facets of a polytope's dual will be the topological duals of the polytope's vertex figures. For
regularIn mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
and
uniformA uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
polytopes, the dual facets will be the polar reciprocals of the original's facets. For example, in four dimensions, the vertex figure of the
600-cell is the
icosahedronIn geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
; the dual of the 600-cell is the
120-cell, whose facets are
dodecahedra, which are the dual of the icosahedron.
Self-dual polytopes and tessellations
The primary class of self-dual polytopes are
regular polytopeIn mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
s with palindromic
Schläfli symbols. All regular polygons, {a} are self-dual,
polyhedraIn elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
of the form {a,a},
4-polytopesIn geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
of the form {a,b,a},
5-polytopeIn five-dimensional geometry, a 5-polytope is a 5-dimensional polytope, bounded by facets. Each polyhedral cell being shared by exactly two polychoron facets. A proposed name for 5-polytopes is polyteron.-Definition:...
s of the form {a,b,b,a}, etc.
The self-dual regular polytopes are:
- All regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s, {a}.
- All regular n-simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
es, {3,3,...,3}
- The regular 24-cell in 4 dimensions, {3,4,3}.
- All regular n-dimensional cubic honeycombs
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
, {4,3,...,3,4}. These may be treated as infinite polytopes.
See also
- Conway polyhedron notation
Conway polyhedron notation is used to describe polyhedra based on a seed polyhedron modified by various operations.The seed polyhedra are the Platonic solids, represented by their first letter of their name ; the prisms , antiprisms and pyramids...
- Dual polygon
In geometry, polygons are associated into pairs called duals, where the vertices of one correspond to the edges of the other.-Properties:Regular polygons are self-dual....
- Self-dual graph
- Self-dual polygon
External links