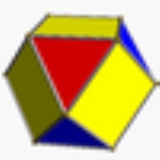
Cuboctahedron
Encyclopedia
In geometry
, a cuboctahedron is a polyhedron
with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron
, i.e. an Archimedean solid
, being vertex-transitive
and edge-transitive.
Its dual polyhedron
is the rhombic dodecahedron
.
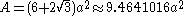
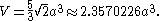
An alternate set of coordinates can be made in 4-space, as 12 permutations of:
This construction exists as one of 16 orthant
facets of the cantellated 16-cell.
A3. With the addition of 6 vertices of the octahedron
, these vertices represent the 18 root vectors simple Lie group
B3.
of a four-dimensional 16-cell
.
A cuboctahedron has octahedral symmetry. Its first stellation
is the compound
of a cube and its dual octahedron
, with the vertices of the cuboctahedron located at the midpoints of the edges of either.
The cuboctahedron is a rectified
cube
and also a rectified octahedron
.
It is also a cantellated
tetrahedron
. With this construction it is given the Wythoff symbol
: 3 3 | 2.
A skew cantellation of the tetrahedron produces a solid with faces parallel to those of the cuboctahedron, namely eight triangles of two sizes, and six rectangles. While its edges are unequal, this solid remains vertex-uniform: the solid has the full tetrahedral symmetry group
and its vertices are equivalent under that group.
The edges of a cuboctahedron form four regular hexagons. If the cuboctahedron is cut in the plane of one of these hexagons, each half is a triangular cupola
, one of the Johnson solid
s; the cuboctahedron itself thus can also be called a triangular gyrobicupola
, the simplest of a series (other than the gyrobifastigium
or "digonal gyrobicupola"). If the halves are put back together with a twist, so that triangles meet triangles and squares meet squares, the result is another Johnson solid, the triangular orthobicupola
.
Both triangular bicupolae are important in sphere packing
. The distance from the solid's centre to its vertices is equal to its edge length. Each central sphere
can have up to twelve neighbors, and in a face-centered cubic lattice these take the positions of a cuboctahedron's vertices. In a hexagonal close-packed lattice they correspond to the corners of the triangular orthobicupola. In both cases the central sphere takes the position of the solid's centre.
Cuboctahedra appear as cells in three of the convex uniform honeycomb
s and in nine of the convex uniform polychora
.
The volume of the cuboctahedron is 5/6 of that of the enclosing cube and 5/8 of that of the enclosing octahedron.
The cuboctahedron shares its edges and vertex arrangement with two nonconvex uniform polyhedra
: the cubohemioctahedron
(having the square faces in common) and the octahemioctahedron
(having the triangular faces in common). It also serves as a cantellated Tetrahedron
, as being a rectified Tetratetrahedron.
The cuboctahedron 2-covers the tetrahemihexahedron
, which accordingly has the same abstract
vertex figure
(2 triangles and two squares: 3.4.3.4) and half the vertices, edges, and faces. (The actual vertex figure of the tetrahemihexahedron is 3.4.3/2.4, with the a/2 factor due to the cross.)
and eight irregular but equal octahedra in the shape of the convex hull of a cube with two opposite vertices removed. This decomposition of the cuboctahedron corresponds with the cell-first parallel projection of the 24-cell into 3 dimensions. Under this projection, the cuboctahedron forms the projection envelope, which can be decomposed into 6 square faces, a regular octahedron, and 8 irregular octahedra. These elements correspond with the images of 6 of the octahedral cells in the 24-cell, the nearest and farthest cells from the 4D viewpoint, and the remaining 8 pairs of cells, respectively.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a cuboctahedron is a polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron
Quasiregular polyhedron
In geometry, a quasiregular polyhedron is a semiregular polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are edge-transitive and hence step closer to regularity than the semiregular which are merely vertex-transitive.There are only two convex...
, i.e. an Archimedean solid
Archimedean solid
In geometry an Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices...
, being vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
and edge-transitive.
Its dual polyhedron
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
is the rhombic dodecahedron
Rhombic dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...
.
Other names
- Heptaparallelohedron (Buckminster FullerBuckminster FullerRichard Buckminster “Bucky” Fuller was an American systems theorist, author, designer, inventor, futurist and second president of Mensa International, the high IQ society....
)- Fuller applied the name "DymaxionDymaxionThe word Dymaxion is a brand name that Buckminster Fuller used for several of his inventions. It is a portmanteau of the words dynamic, maximum, and ion....
" and Vector Equilibrium to this shape, used in an early version of the Dymaxion mapDymaxion mapThe Dymaxion map or Fuller map is a projection of a world map onto the surface of a polyhedron, which can be unfolded and flattened to two dimensions. The projection depicts the earth's continents as "one island," or nearly contiguous land masses. The arrangement heavily interrupts the map in order...
.
- Fuller applied the name "Dymaxion
- With Oh symmetry, it is a rectifiedRectification (geometry)In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
cubeCubeIn geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
or rectified octahedron (Norman Johnson) - With Td symmetry, it is a cantellatedCantellation (geometry)In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs...
tetrahedronTetrahedronIn geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
. - With D3d symmetry, it is a triangular gyrobicupola.
Area and volume
The area A and the volume V of the cuboctahedron of edge length a are: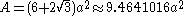
Images
Cartesian coordinates
The Cartesian coordinates for the vertices of a cuboctahedron (of edge length √2) centered at the origin are:- (±1,±1,0)
- (±1,0,±1)
- (0,±1,±1)
An alternate set of coordinates can be made in 4-space, as 12 permutations of:
- (0,1,1,2)
This construction exists as one of 16 orthant
Orthant
In geometry, an orthant or hyperoctant is the analogue in n-dimensional Euclidean space of a quadrant in the plane or an octant in three dimensions....
facets of the cantellated 16-cell.
Root vectors
The cuboctahedron's 12 vertices can represent the root vectors of the simple Lie groupSimple Lie group
In group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
A3. With the addition of 6 vertices of the octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
, these vertices represent the 18 root vectors simple Lie group
Simple Lie group
In group theory, a simple Lie group is a connected non-abelian Lie group G which does not have nontrivial connected normal subgroups.A simple Lie algebra is a non-abelian Lie algebra whose only ideals are 0 and itself...
B3.
Geometric relations
A cuboctahedron can be obtained by taking an appropriate cross sectionCross section (geometry)
In geometry, a cross-section is the intersection of a figure in 2-dimensional space with a line, or of a body in 3-dimensional space with a plane, etc...
of a four-dimensional 16-cell
16-cell
In four dimensional geometry, a 16-cell or hexadecachoron is a regular convex 4-polytope. It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century....
.
A cuboctahedron has octahedral symmetry. Its first stellation
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
is the compound
Polyhedral compound
A polyhedral compound is a polyhedron that is itself composed of several other polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram....
of a cube and its dual octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
, with the vertices of the cuboctahedron located at the midpoints of the edges of either.
The cuboctahedron is a rectified
Rectification (geometry)
In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
and also a rectified octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
.
It is also a cantellated
Cantellation (geometry)
In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs...
tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
. With this construction it is given the Wythoff symbol
Wythoff symbol
In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....
: 3 3 | 2.

A skew cantellation of the tetrahedron produces a solid with faces parallel to those of the cuboctahedron, namely eight triangles of two sizes, and six rectangles. While its edges are unequal, this solid remains vertex-uniform: the solid has the full tetrahedral symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
and its vertices are equivalent under that group.
The edges of a cuboctahedron form four regular hexagons. If the cuboctahedron is cut in the plane of one of these hexagons, each half is a triangular cupola
Triangular cupola
In geometry, the triangular cupola is one of the Johnson solids . It can be seen as half a cuboctahedron.The 92 Johnson solids were named and described by Norman Johnson in 1966.-Formulae:...
, one of the Johnson solid
Johnson solid
In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
s; the cuboctahedron itself thus can also be called a triangular gyrobicupola
Bicupola (geometry)
In geometry, a bicupola is a solid formed by connecting two cupolae on their bases.There are two classes of bicupola because each cupola half is bordered by alternating triangles and squares...
, the simplest of a series (other than the gyrobifastigium
Gyrobifastigium
In geometry, the gyrobifastigium is the 26th Johnson solid . It can be constructed by joining two face-regular triangular prisms along corresponding square faces, giving a half-turn to one prism....
or "digonal gyrobicupola"). If the halves are put back together with a twist, so that triangles meet triangles and squares meet squares, the result is another Johnson solid, the triangular orthobicupola
Triangular orthobicupola
In geometry, the triangular orthobicupola is one of the Johnson solids . As the name suggests, it can be constructed by attaching two triangular cupolas along their bases...
.
Both triangular bicupolae are important in sphere packing
Sphere packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space...
. The distance from the solid's centre to its vertices is equal to its edge length. Each central sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
can have up to twelve neighbors, and in a face-centered cubic lattice these take the positions of a cuboctahedron's vertices. In a hexagonal close-packed lattice they correspond to the corners of the triangular orthobicupola. In both cases the central sphere takes the position of the solid's centre.
Cuboctahedra appear as cells in three of the convex uniform honeycomb
Convex uniform honeycomb
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;...
s and in nine of the convex uniform polychora
Uniform polychoron
In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....
.
The volume of the cuboctahedron is 5/6 of that of the enclosing cube and 5/8 of that of the enclosing octahedron.
Related polyhedra
 Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
 Truncated cube Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... |
 cuboctahedron |
 Truncated octahedron Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
 Octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
The cuboctahedron shares its edges and vertex arrangement with two nonconvex uniform polyhedra
Nonconvex uniform polyhedron
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting...
: the cubohemioctahedron
Cubohemioctahedron
In geometry, the cubohemioctahedron is a nonconvex uniform polyhedron, indexed as U15. Its vertex figure is a crossed quadrilateral.A nonconvex polyhedron has intersecting faces which do not represent new edges or faces...
(having the square faces in common) and the octahemioctahedron
Octahemioctahedron
In geometry, the octahemioctahedron is a nonconvex uniform polyhedron, indexed as U3. Its vertex figure is a crossed quadrilateral.It is one of nine hemipolyhedra with 4 hexagonal faces passing through the model center.- Related polyhedra :...
(having the triangular faces in common). It also serves as a cantellated Tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
, as being a rectified Tetratetrahedron.
 Cuboctahedron |
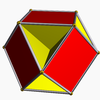 Cubohemioctahedron Cubohemioctahedron In geometry, the cubohemioctahedron is a nonconvex uniform polyhedron, indexed as U15. Its vertex figure is a crossed quadrilateral.A nonconvex polyhedron has intersecting faces which do not represent new edges or faces... |
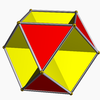 Octahemioctahedron Octahemioctahedron In geometry, the octahemioctahedron is a nonconvex uniform polyhedron, indexed as U3. Its vertex figure is a crossed quadrilateral.It is one of nine hemipolyhedra with 4 hexagonal faces passing through the model center.- Related polyhedra :... |
The cuboctahedron 2-covers the tetrahemihexahedron
Tetrahemihexahedron
In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 6 vertices and 12 edges, and 7 faces: 4 triangular and 3 square. Its vertex figure is a crossed quadrilateral. It has Coxeter-Dynkin diagram of ....
, which accordingly has the same abstract
Abstract polytope
In mathematics, an abstract polytope, informally speaking, is a structure which considers only the combinatorial properties of a traditional polytope, ignoring many of its other properties, such as angles, edge lengths, etc...
vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
(2 triangles and two squares: 3.4.3.4) and half the vertices, edges, and faces. (The actual vertex figure of the tetrahemihexahedron is 3.4.3/2.4, with the a/2 factor due to the cross.)
 Cuboctahedron |
 Tetrahemihexahedron Tetrahemihexahedron In geometry, the tetrahemihexahedron or hemicuboctahedron is a uniform star polyhedron, indexed as U4. It has 6 vertices and 12 edges, and 7 faces: 4 triangular and 3 square. Its vertex figure is a crossed quadrilateral. It has Coxeter-Dynkin diagram of .... |
Related polytopes
The cuboctahedron can be decomposed into a regular octahedronOctahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
and eight irregular but equal octahedra in the shape of the convex hull of a cube with two opposite vertices removed. This decomposition of the cuboctahedron corresponds with the cell-first parallel projection of the 24-cell into 3 dimensions. Under this projection, the cuboctahedron forms the projection envelope, which can be decomposed into 6 square faces, a regular octahedron, and 8 irregular octahedra. These elements correspond with the images of 6 of the octahedral cells in the 24-cell, the nearest and farthest cells from the 4D viewpoint, and the remaining 8 pairs of cells, respectively.
Cultural occurrences
- In the Star TrekStar TrekStar Trek is an American science fiction entertainment franchise created by Gene Roddenberry. The core of Star Trek is its six television series: The Original Series, The Animated Series, The Next Generation, Deep Space Nine, Voyager, and Enterprise...
episode "By Any Other Name", aliens seize the EnterpriseStarship EnterpriseThe Enterprise or USS Enterprise is the name of several fictional starships, some of which are the focal point for various television series and films in the Star Trek franchise created by Gene Roddenberry. It is considered a name of legacy in the fleet...
by transforming crew members into inanimate cuboctahedra.
- The "Geo Twister" fidget toy http://www.trainerswarehouse.com/prodinfo.asp?number=FIGEO is a flexible cuboctahedron.
See also
- CubeCubeIn geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
- IcosidodecahedronIcosidodecahedronIn geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
- OctahedronOctahedronIn geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
- RhombicuboctahedronRhombicuboctahedronIn geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles...
- Truncated cuboctahedronTruncated cuboctahedronIn geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges...
External links
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- Editable printable net of a Cuboctahedron with interactive 3D view

