
Wythoff symbol
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction
Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
applied to Schwarz triangle
Schwarz triangle
In geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in ....
s.
A Schwarz triangle is a triangle that covers the sphere or the plane a finite number of times by reflection in its edges. The usual representation for the triangle is three numbers - integers or fractions - where π/x represents the angle at that vertex. For example, the triangle (2 3 4) represents the symmetry of a cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
, while (5/2 5/2 5/2) is the face of an icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
.
Wythoff's construction in three dimensions is by placing a vertex in the triangle, and dropping perpendiculars to each of the edges. The uniform cases must exist in all cases, correspond to when the perpendiculars are either 0 (giving no edge) or 1 (giving a unit edge).
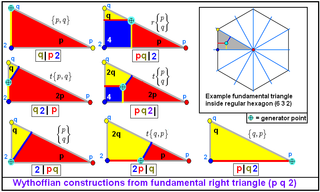
The edges of the triangle opposite an angle are named after the angle, so an edge opposite the right angle would be designated '2'. The symbol then corresponds to a representation of off | on. Each of the numbers p in the symbol becomes a polygon pn, where n is the number of other edges that appear before the bar. So in 3 | 4 2, at the 3 corner of the triangle forms a point (literally something with 3*0 sides), while the 4 gives 4*1 = square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
the digon
Digon
In geometry, a digon is a polygon with two sides and two vertices. It is degenerate in a Euclidean space, but may be non-degenerate in a spherical space.A digon must be regular because its two edges are the same length...
2*1 disappears as an edge.
The special case of the snub
Snub (geometry)
In geometry, an alternation is an operation on a polyhedron or tiling that removes alternate vertices. Only even-sided polyhedra can be alternated, for example the zonohedra. Every 2n-sided face becomes n-sided...
figures is done by using the symbol | p q r. This would normally evaluate as the point in the centre of the sphere. The faces of a snub alternate as p 3 q 3 r 3. This gives an antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
when q=r=2.
Each symbol represents one uniform polyhedron
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
or tiling, although the same tiling/polyhedron can have different Wythoff symbols from different symmetry generators. For example, the regular cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
can be represented by 3 | 4 2 with Oh symmetry
Octahedral symmetry
150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...
, and 2 4 | 2 as a square prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
with 2 colors and D4h symmetry, as well as 2 2 2 | with 3 colors and D2h symmetry.
It can be applied with a slight extension to all uniform polyhedra, but the construction methods do not lead to all uniform tilings in euclidean or hyperbolic space.
Summary table
| General | Right triangle (r=2) | ||||
|---|---|---|---|---|---|
| Description | Wythoff symbol |
Vertex configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
Wythoff symbol |
Vertex configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
Schläfli symbol |
| regular Regular polyhedron A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags... and quasiregular Quasiregular polyhedron In geometry, a quasiregular polyhedron is a semiregular polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are edge-transitive and hence step closer to regularity than the semiregular which are merely vertex-transitive.There are only two convex... |
q | p r | (p.r)q | q | p 2 | pq | {p,q} |
| p | q r | (q.r)p | p | q 2 | qp | {q,p} | |
| r | p q | (q.p)r | 2 | p q | (q.p)² | t1{p,q} | |
| truncated Truncation (geometry) In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :... and expanded Expansion (geometry) In geometry, expansion is a polytope operation where facets are separated and moved radially apart, and new facets are formed at separated elements... |
q r | p | q.2p.r.2p | q 2 | p | q.2p.2p | t0,1{p,q} |
| p r | q | p. 2q.r.2q | p 2 | q | p. 2q.2q | t0,1{q,p} | |
| p q | r | 2r.q.2r.p | p q | 2 | 4.q.4.p | t0,2{p,q} | |
| even-faced Zonohedron A zonohedron is a convex polyhedron where every face is a polygon with point symmetry or, equivalently, symmetry under rotations through 180°. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional... |
p q r | | 2r.2q.2p | p q 2 | | 4.2q.2p | t0,1,2{p,q} |
| p q (r s) | | 2p.2q.-2p.-2q | p 2 (r s) | | 2p.4.-2p.4/3 | ||
| snub Snub (geometry) In geometry, an alternation is an operation on a polyhedron or tiling that removes alternate vertices. Only even-sided polyhedra can be alternated, for example the zonohedra. Every 2n-sided face becomes n-sided... |
| p q r | 3.r.3.q.3.p | | p q 2 | 3.3.q.3.p | s{p,q} |
| | p q r s | (4.p. 4.q.4.r.4.s)/2 | - | - |
There are three special cases:
- p q (r s) | – This is a mixture of p q r | and p q s |.
- | p q r – Snub forms (alternated) are give this otherwise unused symbol.
- | p q r s – A unique snub form for U75Great dirhombicosidodecahedronIn geometry, the great dirhombicosidodecahedron is a nonconvex uniform polyhedron, indexed last as U75.This is the only uniform polyhedron with more than six faces meeting at a vertex...
that isn't Wythoff-constructible.
Description
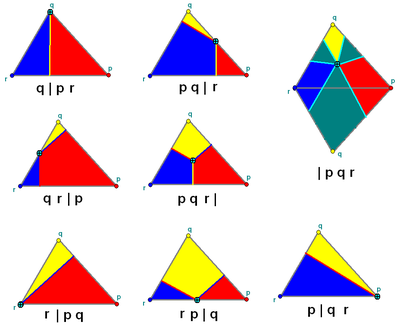
The numbers p,q,r describe the fundamental triangle of the symmetry group: at its vertices, the generating mirrors meet in angles of π/p, π/q, π/r. On the sphere there are 3 main symmetry types: (3 3 2), (4 3 2), (5 3 2), and one infinite family (p 2 2), for any p. (All simple families have one right angle and so r=2.)The position of the vertical bar in the symbol specifies a categorical position of the generator point within the fundamental triangle. The generator point can either be on or off each mirror, activated or not. This distinction creates 8 (2³) possible forms, neglecting one where the generator point is on all the mirrors.
In this notation the mirrors are labeled by the reflection-order of the opposite vertex. The p,q,r values are listed before the bar if the corresponding mirror is active.
The one impossible symbol | p q r implies the generator point is on all mirrors, which is only possible if the triangle is degenerate, reduced to a point. This unused symbol is therefore arbitrarily reassigned to represent the case where all mirrors are active, but odd-numbered reflected images are ignored. The resulting figure has rotational symmetry only.
This symbol is functionally similar to the more general Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
, in which each node represents a mirror and the arcs between them – marked with numbers – the angles between the mirrors. (An arc representing a right angle is omitted.) A node is circled if the generator point is not on the mirror.
Symmetry triangles
There are 4 symmetry classes of reflection on the sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, and two in the Euclidean plane. A few of the infinitely many such patterns in the hyperbolic plane
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
are also listed. (Increasing any of the numbers defining a hyperbolic or Euclidean tiling makes another hyperbolic tiling.)
- (p 2 2) dihedral symmetryDihedral symmetry in three dimensionsThis article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:...
, p = 2, 3, 4... (order 4p) - (3 3 2) tetrahedral symmetryTetrahedral symmetry150px|right|thumb|A regular [[tetrahedron]], an example of a solid with full tetrahedral symmetryA regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.The group of all symmetries is isomorphic to the group...
(order 24) - (3 3 3) *333 symmetry (Euclidean plane)
- (4 3 2) octahedral symmetryOctahedral symmetry150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...
(order 48) - (4 3 3) *433 symmetry (hyperbolic plane)
- (4 4 2) *442 symmetry: 45°-45°-90° triangle
- (4 4 3) *443 symmetry (hyperbolic plane)
- (5 3 2) icosahedral symmetryIcosahedral symmetryA regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
(order 120) - (5 4 2) *542 symmetry (hyperbolic plane)
- (6 3 2) *632 symmetry: 30°-60°-90° triangle
- (7 3 2) *732 symmetry (hyperbolic plane)
| Dihedral spherical | Spherical | |||
|---|---|---|---|---|
| D2h | D3h | Td | Oh | Ih |
| *222 | *322 | *332 | *432 | *532 |
 (2 2 2) |
 (3 2 2) |
 ( 3 3 2) |
 (4 3 2) |
 (5 3 2) |
The above symmetry groups only includes the integer solutions on the sphere. The list of Schwarz triangle
Schwarz triangle
In geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in ....
s includes rational numbers, and determine the full set of solutions of nonconvex uniform polyhedra
Nonconvex uniform polyhedron
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting...
.
| p4m | p3m | p6m |
|---|---|---|
| *442 | *333 | *632 |
 (4 4 2) |
 (3 3 3) |
 (6 3 2) |
| *732 | *542 | *433 |
|---|---|---|
 (7 3 2) |
 (5 4 2) |
 (4 3 3) |
In the tilings above, each triangle is a fundamental domain, colored by even and odd reflections.
Summary spherical and plane tilings
Selected tilings created by the Wythoff construction are given below.Spherical tilings (r = 2)
| (p q 2) | Fund. triangles |
Parent | Truncated | Rectified | Bitruncated | Birectified (dual) |
Cantellated | Omnitruncated (Cantitruncated) |
Snub |
|---|---|---|---|---|---|---|---|---|---|
| Wythoff symbol Wythoff construction In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :... |
q | p 2 | 2 q | p | 2 | p q | 2 p | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 | |
| Schläfli symbol | t0{p,q} | t0,1{p,q} | t1{p,q} | t1,2{p,q} | t2{p,q} | t0,2{p,q} | t0,1,2{p,q} | s{p,q} | |
| Coxeter–Dynkin diagram | |||||||||
| Vertex figure Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
pq | (q.2p.2p) | (p.q.p.q) | (p. 2q.2q) | qp | (p. 4.q.4) | (4.2p.2q) | (3.3.p. 3.q) | |
| Tetrahedral (3 3 2) |
 |
{3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
 (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
(3.3a.3.3a) Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
 (3.6.6) Truncated tetrahedron In geometry, the truncated tetrahedron is an Archimedean solid. It has 4 regular hexagonal faces, 4 regular triangular faces, 12 vertices and 18 edges.- Area and volume :... |
 {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
 (3a.4.3b.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
 (4.6a.6b) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
 (3.3.3a.3.3b) Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
| Octahedral (4 3 2) |
 |
 {4,3} Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
 (3.8.8) Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices.... |
 (3.4.3.4) Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,... |
 (4.6.6) Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron.... |
 {3,4} Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
 (3.4.4a.4) Rhombicuboctahedron In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles... |
 (4.6.8) Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges... |
 (3.3.3a.3.4) Snub cube In geometry, the snub cube, or snub cuboctahedron, is an Archimedean solid.The snub cube has 38 faces, 6 of which are squares and the other 32 are equilateral triangles. It has 60 edges and 24 vertices. It is a chiral polyhedron, that is, it has two distinct forms, which are mirror images of each... |
| Icosahedral (5 3 2) |
 |
 {5,3} |
 (3.10.10) Truncated dodecahedron In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :... |
 (3.5.3.5) Icosidodecahedron In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon... |
 (5.6.6) Truncated icosahedron In geometry, the truncated icosahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids whose faces are two or more types of regular polygons.It has 12 regular pentagonal faces, 20 regular hexagonal faces, 60 vertices and 90 edges.... |
 {3,5} Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
 (3.4.5.4) Rhombicosidodecahedron In geometry, the rhombicosidodecahedron, or small rhombicosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed of two or more types of regular polygon faces.... |
 (4.6.10) Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
 (3.3.3a.3.5) Snub dodecahedron In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... |
Dihedral symmetry (q = r = 2)
Spherical tilings with dihedral symmetry exist for all p = 2, 3, 4, ... many with digonDigon
In geometry, a digon is a polygon with two sides and two vertices. It is degenerate in a Euclidean space, but may be non-degenerate in a spherical space.A digon must be regular because its two edges are the same length...
faces which become degenerate polyhedra. Two of the eight forms (Rectified and cantellated) are replications and are skipped in the table.
| (p 2 2) | Fund. triangles |
Parent | Truncated | Bitruncated (truncated dual) |
Birectified (dual) |
Omnitruncated (Cantitruncated) |
Snub | ||
|---|---|---|---|---|---|---|---|---|---|
| Extended Schläfli symbol |
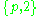 |
 |
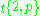 |
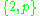 |
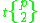 |
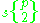 |
|||
| t0{p,2} | t0,1{p,2} | t1,2{p,2} | t2{p,2} | t0,1,2{p,2} | s{p,2} | ||||
| Wythoff symbol | 2 | p 2 | 2 2 | p | 2 p | 2 | p | 2 2 | p 2 2 | | | p 2 2 | |||
| Coxeter–Dynkin diagram | |||||||||
| Vertex figure Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
p² | (2.2p.2p) | (p.p) | 2p | (4.2p.4) | (3.3.p. 3) | |||
| (2 2 2) |  |
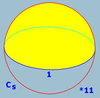 {2,2} Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is... |
2.4.4 Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is... |
4.4.2 Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is... |
 {2,2} |
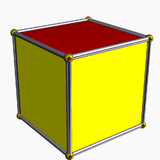 4.4.4 Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... |
 3.3.3.2 Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
||
| (3 2 2) |  |
 {3,2} Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is... |
 2.6.6 Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is... |
 4.4.3 Triangular prism In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides.... |
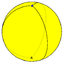 {2,3} |
 4.4.6 Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
 3.3.3.3 Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
||
| (4 2 2) | {4,2} Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is... |
2.8.8 Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is... |
 4.4.4 |
{2,4} |  4.4.8 |
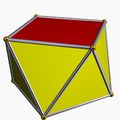 3.3.3.4 |
|||
| (5 2 2) | {5,2} Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is... |
2.10.10 Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is... |
 4.4.5 Pentagonal prism In geometry, the pentagonal prism is a prism with a pentagonal base. It is a type of heptahedron with 7 faces, 15 edges, and 10 vertices.- As a semiregular polyhedron :... |
{2,5} |  4.4.10 Decagonal prism In geometry, the decagonal prism is the eighth in an infinite set of prisms, formed by ten square side faces and two regular decagon caps. With twelve faces, it is one of many nonregular dodecahedra.If faces are all regular, it is a semiregular polyhedron.... |
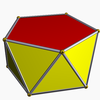 3.3.3.5 Pentagonal antiprism In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces... |
|||
| (6 2 2) |  {6,2} Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is... |
2.12.12 Dihedron A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is... |
 4.4.6 Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces... |
 {2,6} |
 4.4.12 Dodecagonal prism In geometry, the dodecagonal prism is the tenth in an infinite set of prisms, formed by square sides and two regular dodecagon caps.If faces are all regular, it is a semiregular polyhedron.- Use :... |
 3.3.3.6 Hexagonal antiprism In geometry, the hexagonal antiprism is the 4th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- See also :* Set of antiprisms... |
|||
| ... | |||||||||
Planar tilings (r = 2)
One representative hyperbolic tiling is given, and shown as a Poincaré diskPoincaré disk model
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of n-dimensional hyperbolic geometry in which the points of the geometry are in an n-dimensional disk, or unit ball, and the straight lines of the hyperbolic geometry are segments of circles contained in the disk...
projection.
| (p q 2) | Fund. triangles |
Parent | Truncated | Rectified | Bitruncated | Birectified (dual) |
Cantellated | Omnitruncated (Cantitruncated) |
Snub |
|---|---|---|---|---|---|---|---|---|---|
| Wythoff symbol Wythoff construction In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :... |
q | p 2 | 2 q | p | 2 | p q | 2 p | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 | |
| Schläfli symbol | t0{p,q} | t0,1{p,q} | t1{p,q} | t1,2{p,q} | t2{p,q} | t0,2{p,q} | t0,1,2{p,q} | s{p,q} | |
| Coxeter–Dynkin diagram | |||||||||
| Vertex figure Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
pq | (q.2p.2p) | (p.q.p.q) | (p. 2q.2q) | qp | (p. 4.q.4) | (4.2p.2q) | (3.3.p. 3.q) | |
| Square tiling (4 4 2) |
 V4.8.8 Tetrakis square tiling In geometry, the tetrakis square tiling is a tiling of the Euclidean plane. It is square tiling with each square divided into four triangles from the center point, forming an infinite arrangement of lines.... |
 {4,4} |
 4.8.8 Truncated square tiling In geometry, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon... |
 4.4a.4.4a |
 4.8.8 Truncated square tiling In geometry, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon... |
 {4,4} |
 4.4a.4b.4a |
 4.8.8 Truncated square tiling In geometry, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon... |
 3.3.4a.3.4b |
| (Hyperbolic plane) (5 4 2) |
 |
 {5,4} |
 4.10.10 |
 4.5.4.5 |
 5.8.8 |
 {4,5} |
 4.4.5.4 |
 4.8.10 |
 3.3.4.3.5 |
| (Hyperbolic plane) (5 5 2) |
 |
 {5,5} |
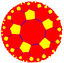 5.10.10 |
 5.5.5.5 |
 5.10.10 |
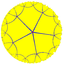 {5,5} |
 4.4.5.4 |
 4.10.10 |
 3.3.5.3.5 |
| Hexagonal tiling (6 3 2) |
 V4.6.12 |
 {6,3} |
 3.12.12 Truncated hexagonal tiling In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons and one triangle on each vertex.... |
 3.6.3.6 Trihexagonal tiling In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex... |
 6.6.6 |
 {3,6} |
 3.4.6.4 |
 4.6.12 |
 3.3.3.3.6 Snub hexagonal tiling In geometry, the Snub hexagonal tiling is a semiregular tiling of the Euclidean plane. There are four triangles and one hexagon on each vertex... |
| (Hyperbolic plane) (7 3 2) |
 |
 {7,3} |
 3.14.14 |
 3.7.3.7 Triheptagonal tiling In geometry, the triheptagonal tiling is a semiregular tiling of the hyperbolic plane, representing a rectified Order-3 heptagonal tiling. There are two triangles and two heptagons alternating on each vertex... |
 7.6.6 |
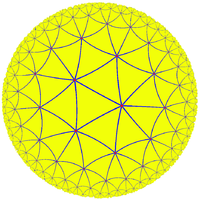 {3,7} |
 3.4.7.4 |
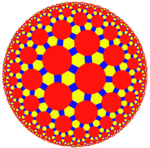 4.6.14 |
 3.3.3.3.7 |
| (Hyperbolic plane) (8 3 2) |
 |
 {8,3} |
 3.16.16 |
 3.8.3.8 |
 8.6.6 |
 {3,8} |
 3.4.8.4 |
 4.6.16 |
 3.3.3.3.8 |
| (Hyperbolic plane) (∞ 3 2) |
|||||||||
| (Hyperbolic plane) (∞ 4 2) |
|||||||||
| (Hyperbolic plane) (∞ ∞ 2) |
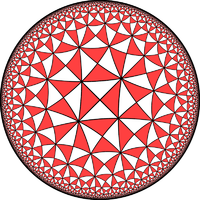
Planar tilings (r > 2)
The Coxeter–Dynkin diagram is given in a linear form, although it is actually a triangle, with the trailing segment r connecting to the first node.| Wythoff symbol Wythoff construction In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :... (p q r) |
Fund. triangles |
q | p r | r q | p | r | p q | r p | q | p | q r | p q | r | p q r | | | p q r |
|---|---|---|---|---|---|---|---|---|---|
| Coxeter–Dynkin diagram | |||||||||
| Vertex figure Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
(p.q)r | (r.2p.q.2p) | (p.r)q | (q.2r.p. 2r) | (q.r)p | (p.2q.r.2q) | (2p.2q.2r) | (3.r.3.q.3.p) | |
| Triangular (3 3 3) |
 |
 (3.3)3 |
 3.6.3.6 Trihexagonal tiling In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex... |
 (3.3)3 |
 3.6.3.6 Trihexagonal tiling In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex... |
 (3.3)3 |
 3.6.3.6 Trihexagonal tiling In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex... |
 6.6.6 |
 3.3.3.3.3.3 |
| Hyperbolic (4 3 3) |
 |
 (3.4)³ |
 3.8.3.8 |
 (3.4)³ |
 3.6.4.6 |
 (3.3)4 |
 3.6.4.6 |
 6.6.8 |
 3.3.3.3.3.4 |
| Hyperbolic (4 4 3) |
 |
 (3.4)4 |
 3.8.4.8 |
 (3.4)4 |
 3.6.4.6 |
 (3.4)4 |
 4.6.4.6 |
 6.8.8 |
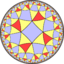 3.3.3.4.3.4 |
| Hyperbolic (4 4 4) |
 |
 (4.4)4 |
 4.8.4.8 |
 (4.4)4 |
 4.8.4.8 |
 (4.4)4 |
 4.8.4.8 |
 8.8.8 |
 3.4.3.4.3.4 |
| Hyperbolic (3 3 ∞) |
|||||||||
| Hyperbolic (3 ∞ ∞) |
|||||||||
| Hyperbolic (∞ ∞ ∞) |
Overlapping spherical tilings (r = 2)
Tilings are shown as polyhedraPolyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
. Some of the forms are degenerate, given with brackets for vertex figure
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
s, with overlapping edges or verices.
| (p q 2) | Fund. triangle |
Parent | Truncated | Rectified | Bitruncated | Birectified (dual) |
Cantellated | Omnitruncated (Cantitruncated) |
Snub |
|---|---|---|---|---|---|---|---|---|---|
| Wythoff symbol Wythoff construction In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :... |
q | p 2 | 2 q | p | 2 | p q | 2 p | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 | |
| Schläfli symbol | t0{p,q} | t0,1{p,q} | t1{p,q} | t1,2{p,q} | t2{p,q} | t0,2{p,q} | t0,1,2{p,q} | s{p,q} | |
| Coxeter–Dynkin diagram | |||||||||
| Vertex figure Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
pq | (q.2p.2p) | (p.q.p.q) | (p. 2q.2q) | qp | (p. 4.q.4) | (4.2p.2q) | (3.3.p. 3.q) | |
| Icosahedral (5/2 3 2) |
 {3,5/2} |
 (5/2.6.6) |
 (3.5/2)2 |
 [3.10/2.10/2 Small complex icosidodecahedron In geometry, the small complex icosidodecahedron is a degenerate uniform star polyhedron. It has 32 faces , 60 edges and 12 vertices... ] |
 {5/2,3} |
 [3.4.5/2.4 Small complex rhombicosidodecahedron In geometry, the small complex rhombicosidodecahedron is a degenerate uniform star polyhedron. It has 62 faces , 120 edges and 20 vertices... ] |
 [4.10/2.6 Rhombicosahedron In geometry, the rhombicosahedron is a nonconvex uniform polyhedron, indexed as U56. Its vertex figure is an antiparallelogram.- Related polyhedra :... ] |
 (3.3.3.3.5/2) |
|
| Icosahedral (5 5/2 2) |
 {5,5/2} |
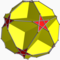 (5/2.10.10) |
 (5/2.5)2 |
 [5.10/2.10/2] |
 {5/2,5} |
 (5/2.4.5.4) |
 [4.10/2.10 Small rhombidodecahedron In geometry, the small rhombidodecahedron is a nonconvex uniform polyhedron, indexed as U39. Its vertex figure is a crossed quadrilateral.- Related polyhedra :... ] |
 (3.3.5/2.3.5) |
See also
- Regular polytopeRegular polytopeIn mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...
- Regular polyhedronRegular polyhedronA regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
- List of uniform tilings
- List of uniform polyhedra
External links
- The Wythoff symbol
- Wythoff symbol
- Displays Uniform Polyhedra using Wythoff's construction method
- Description of Wythoff Constructions
- KaleidoTile 3 Free educational software for Windows by Jeffrey WeeksJeffrey Weeks (mathematician)Jeffrey Renwick Weeks is an American mathematician, a geometric topologist and cosmologist.-Biography:Weeks received his B.A. from Dartmouth College in 1978, and his Ph.D. in mathematics from Princeton University in 1985, under the supervision of William Thurston...
that generated many of the images on the page.

