
Small complex rhombicosidodecahedron
Encyclopedia
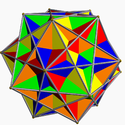
In geometry, the small complex rhombicosidodecahedron (also known as the small complex ditrigonal rhombicosidodecahedron) is a degenerate uniform star polyhedron. It has 62 faces (20 triangle
s, 12 pentagram
s and 30 square
s), 120 (doubled) edges and 20 vertices. All edges are doubled (making it degenerate), sharing 4 faces, but are considered as two overlapping edges as a topological polyhedron.
It can be constructed from the vertex figure (5/2.4.3.4)3, thus making it look identical to the cantellated
great icosahedron.
, U30, and the compound of five cubes
. It is also a facetting
of the dodecahedron.
of the great icosahedron (or, equivalently, of the great stellated dodecahedron).
and the compound of five cubes) with vertex figure (5/3.4.5.4)/3 and the great complex rhombicosidodecahedron (a compound of the great ditrigonal icosidodecahedron and the compound of five cubes) with vertex figure (5/4.4.3/2.4)/3. All three degenerate uniform polyhedra have each vertex really being three coincident vertices and each edge really being two coincident edges.
They can all be constructed by cantellating regular polyhedra.
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s, 12 pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
s and 30 square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
s), 120 (doubled) edges and 20 vertices. All edges are doubled (making it degenerate), sharing 4 faces, but are considered as two overlapping edges as a topological polyhedron.
It can be constructed from the vertex figure (5/2.4.3.4)3, thus making it look identical to the cantellated
Cantellation (geometry)
In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs...
great icosahedron.
As a compound
It can be seen as a compound of the small ditrigonal icosidodecahedronSmall ditrigonal icosidodecahedron
In geometry, the small ditrigonal icosidodecahedron is a nonconvex uniform polyhedron, indexed as U30.-Related polyhedra:Its convex hull is a regular dodecahedron...
, U30, and the compound of five cubes
Compound of five cubes
This polyhedral compound is a symmetric arrangement of five cubes. This compound was first described by Edmund Hess in 1876.It is one of five regular compounds, and dual to the compound of five octahedra....
. It is also a facetting
Facetting
In geometry, facetting is the process of removing parts of a polygon, polyhedron or polytope, without creating any new vertices.Facetting is the reciprocal or dual process to stellation...
of the dodecahedron.
 |
 |
 |
| Small ditrigonal icosidodecahedron Small ditrigonal icosidodecahedron In geometry, the small ditrigonal icosidodecahedron is a nonconvex uniform polyhedron, indexed as U30.-Related polyhedra:Its convex hull is a regular dodecahedron... |
Compound of five cubes Compound of five cubes This polyhedral compound is a symmetric arrangement of five cubes. This compound was first described by Edmund Hess in 1876.It is one of five regular compounds, and dual to the compound of five octahedra.... |
Compound |
As a cantellation
It can also be seen as a cantellationCantellation (geometry)
In geometry, a cantellation is an operation in any dimension that cuts a regular polytope at its edges and vertices, creating a new facet in place of each edge and vertex. The operation also applies to regular tilings and honeycombs...
of the great icosahedron (or, equivalently, of the great stellated dodecahedron).
| (p q 2) | Fund. triangle |
Parent | Truncated | Rectified | Bitruncated | Birectified (dual) |
Cantellated | Omnitruncated (Cantitruncated) |
Snub |
|---|---|---|---|---|---|---|---|---|---|
| Wythoff symbol Wythoff construction In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :... |
q | p 2 | 2 q | p | 2 | p q | 2 p | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 | |
| Schläfli symbol | t0{p,q} | t0,1{p,q} | t1{p,q} | t1,2{p,q} | t2{p,q} | t0,2{p,q} | t0,1,2{p,q} | s{p,q} | |
| Coxeter–Dynkin diagram | |||||||||
| Vertex figure Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
pq | (q.2p.2p) | (p.q.p.q) | (p. 2q.2q) | qp | (p. 4.q.4) | (4.2p.2q) | (3.3.p. 3.q) | |
| Icosahedral (5/2 3 2) |
 {3,5/2} |
 (5/2.6.6) |
 (3.5/2)2 |
 [3.10/2.10/2 Small complex icosidodecahedron In geometry, the small complex icosidodecahedron is a degenerate uniform star polyhedron. It has 32 faces , 60 edges and 12 vertices... ] |
 {5/2,3} |
 [3.4.5/2.4] |
 [4.10/2.6 Rhombicosahedron In geometry, the rhombicosahedron is a nonconvex uniform polyhedron, indexed as U56. Its vertex figure is an antiparallelogram.- Related polyhedra :... ] |
 (3.3.3.3.5/2) |
Related degenerate uniform polyhedra
Two other degenerate uniform polyhedra are also facettings of the dodecahedron. They are the complex rhombidodecadodecahedron (a compound of the ditrigonal dodecadodecahedronDitrigonal dodecadodecahedron
In geometry, the Ditrigonal dodecadodecahedron is a nonconvex uniform polyhedron, indexed as U41.- Related polyhedra :Its convex hull is a regular dodecahedron...
and the compound of five cubes) with vertex figure (5/3.4.5.4)/3 and the great complex rhombicosidodecahedron (a compound of the great ditrigonal icosidodecahedron and the compound of five cubes) with vertex figure (5/4.4.3/2.4)/3. All three degenerate uniform polyhedra have each vertex really being three coincident vertices and each edge really being two coincident edges.
They can all be constructed by cantellating regular polyhedra.
See also
- Small complex icosidodecahedronSmall complex icosidodecahedronIn geometry, the small complex icosidodecahedron is a degenerate uniform star polyhedron. It has 32 faces , 60 edges and 12 vertices...
- Great complex icosidodecahedronGreat complex icosidodecahedronIn geometry, the great complex icosidodecahedron is a degenerate uniform star polyhedron. It has 12 vertices, and 60 edges, and 32 faces, 12 pentagrams and 20 pentagons...
- Complex rhombidodecadodecahedron
- Great complex rhombicosidodecahedron

