In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a Wythoff construction, named after mathematician Willem Abraham Wythoff

Willem Abraham Wythoff

Willem Abraham Wythoff was a Dutch mathematician and number theorist. Wythoff is well-known for his study of a combinatorial game referred to as Wythoff's game and for the Wythoff construction and the Wythoff symbol utilised in this tiling construction.- References :*...

, is a method for constructing a uniform polyhedron

Uniform polyhedron

A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...

 or plane tiling. It is often referred to as Wythoff's kaleidoscopic

Kaleidoscope

A kaleidoscope is a circle of mirrors containing loose, colored objects such as beads or pebbles and bits of glass. As the viewer looks into one end, light entering the other end creates a colorful pattern, due to the reflection off the mirrors...

 construction.

Construction process

It is based on the idea of tiling

Tessellation

A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...

 a sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

, with spherical triangles – see Schwarz triangle

Schwarz triangle

In geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in ....

s. If three mirrors were to be arranged so that their planes intersected at a single point, then the mirrors would enclose a spherical triangle on the surface of any sphere centered on that point and repeated reflections would produce a multitude of copies of the triangle. If the angles of the spherical triangle are chosen appropriately, the triangles will tile the sphere, one or more times.

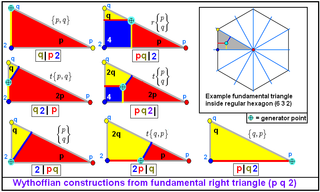
If one places a vertex at a suitable point inside the spherical triangle enclosed by the mirrors, it is possible to ensure that the reflections of that point produce a uniform polyhedron. For a spherical triangle ABC we have four possibilities which will produce a uniform polyhedron:

1. A vertex is placed at the point A. This produces a polyhedron with Wythoff symbol a|b c, where a equals π divided by the angle of the triangle at A, and similarly for b and c.
2. A vertex is placed at a point on line AB so that it bisects
   Bisection
   In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector. The most often considered types of bisectors are the segment bisector and the angle bisector In geometry, bisection is the division of something into two equal...
   
    the angle at C. This produces a polyhedron with Wythoff symbol a b|c.
3. A vertex is placed so that it is on the incentre of ABC. This produces a polyhedron with Wythoff symbol a b c|.
4. The vertex is at a point such that, when it is rotated around any of the triangle's corners by twice the angle at that point, it is displaced by the same distance for every angle. Only even-numbered reflections of the original vertex are used. The polyhedron has the Wythoff symbol |a b c.

The process in general also applies for higher dimensional regular polytope

Regular polytope

In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...

s, including the 4-dimensional uniform polychora

Uniform polychoron

In geometry, a uniform polychoron is a polychoron or 4-polytope which is vertex-transitive and whose cells are uniform polyhedra....

.

Examples

The hexagonal prism Hexagonal prism In geometry, the hexagonal prism is a prism with hexagonal base. The shape has 8 faces, 18 edges, and 12 vertices.Since it has eight faces, it is an octahedron. However, the term octahedron is primarily used to refer to the regular octahedron, which has eight triangular faces...  is constructed from both the (6 2 2) and (3 2 2) families.

The truncated square tiling Truncated square tiling In geometry, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon...  is constructed by two different symmetry positions in the (4 4 2) family.

Non-Wythoffian constructions

Uniform polytope

Uniform polytope

A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....

s that can't be created through a Wythoff mirror construction are called non-Wythoffian. They generally can be derived from Wythoffian forms either by alternation (deletion of alternate vertices) or by insertion of alernating layers of partial figures. Both of these types of figures will contain rotational symmetry. Sometimes snub

Snub (geometry)

In geometry, an alternation is an operation on a polyhedron or tiling that removes alternate vertices. Only even-sided polyhedra can be alternated, for example the zonohedra. Every 2n-sided face becomes n-sided...

 forms are considered Wythoffian, even though they can only be constructed by the alternation of omnitruncated forms.

Examples

The hexagonal antiprism Hexagonal antiprism In geometry, the hexagonal antiprism is the 4th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- See also :* Set of antiprisms...  is constructed by an alternation of a dodecagonal prism Dodecagonal prism In geometry, the dodecagonal prism is the tenth in an infinite set of prisms, formed by square sides and two regular dodecagon caps.If faces are all regular, it is a semiregular polyhedron.- Use :... .

The elongated triangular tiling Elongated triangular tiling In geometry, the elongated triangular tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex.Conway calls it a isosnub quadrille....  is constructed by a layering of square tiling and triangular tiling rows.

The great dirhombicosidodecahedron Great dirhombicosidodecahedron In geometry, the great dirhombicosidodecahedron is a nonconvex uniform polyhedron, indexed last as U75.This is the only uniform polyhedron with more than six faces meeting at a vertex...  is the only non-Wythoffian uniform polyhedron.

See also

• Wythoff symbol
  Wythoff symbol
  In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....
  
   - a symbol for the Wythoff construction of uniform polyhedra
  Uniform polyhedron
  A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
  
   and uniform tiling
  Uniform tiling
  In geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-uniform.Uniform tilings can exist in both the Euclidean plane and hyperbolic plane...
  
  s.
• Coxeter-Dynkin diagram
  Coxeter-Dynkin diagram
  In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
  
   - a generalized symbol for the Wythoff construction of uniform polytope
  Uniform polytope
  A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
  
  s and honeycombs.

External links

• Displays Uniform Polyhedra using Wythoff's construction method
• Description of Wythoff Constructions
• "Jenn", software that generates views of (spherical) polyhedra and polychora from symmetry groups