Bisection
Encyclopedia
In geometry
, bisection is the division of something into two equal or congruent
parts, usually by a line
, which is then called a bisector. The most often considered types of bisectors are the segment bisector (a line that passes through the midpoint of a given segment) and the angle bisector (a line that passes through the apex of an angle, that divides it into two equal angles).
In three dimensional space, bisection is usually done by a plane, also called the bisector or bisecting plane.
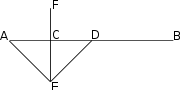A line segment
bisector passes through the midpoint
of the segment.
Particularly important is the perpendicular
bisector of a segment, which, according to its name, meets the segment at right angle
s. The perpendicular bisector of a segment also has the property that each of its points is equidistant
from the segment's endpoints. Therefore Voronoi diagram
boundaries consist of segments of such lines or planes.
In classical geometry, the bisection is a simple compass and straightedge
, whose possibility depends on the ability to draw circle
s of equal radii and different centers. The segment is bisected by drawing intersecting circles of equal radius, whose centers are the endpoints of the segment. The line determined by the points of intersection is the perpendicular bisector, and crosses our original segment at its center. This construction is in fact used when constructing a line perpendicular to a given line at a given point: drawing an arbitrary circle whose center is that point, it intersects the line in two more points, and the perpendicular to be constructed is the one bisecting the segment defined by these two points.
bisector divides the angle into two angles with equal measures. An angle only has one bisector. Each point of an angle bisector is equidistant from the sides of the angle.
The interior bisector of an angle is the half-line or line segment that divides an angle of less than 180° into two equal angles. The exterior bisector is the half-line that divides the opposite angle (of greater than 180°) into two equal angles.
To bisect an angle with straightedge and compass, one draws a circle whose center is the vertex. The circle meets the angle at two points: one on each leg. Using each of these points as a center, draw two circles of the same size. The intersection of the circles (two points) determines a line that is the angle bisector.
The proof of the correctness of these two constructions is fairly intuitive, relying on the symmetry of the problem. It is interesting to note that the trisection of an angle (dividing it into three equal parts) cannot be achieved with the ruler and compass alone (this was first proved by Pierre Wantzel
).
are concurrent in a point called the incenter of the triangle.
If the side lengths of a triangle are
, the semiperimeter (
) is 
, and A is the angle opposite side 
, the length of the internal bisector of angle A is
.
If the bisector of angle A in triangle ABC has length
and if this bisector divides the side opposite A into segments of lengths m and n, then
where b and c are the side lengths opposite vertices B and C; and the side opposite A is divided in the proportion b:c.
If the bisectors of angles A, B, and C have lengths
and 
, then
The angle bisector theorem
is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.
. Three of them are the medians
of the triangle (which connect the sides' midpoints with the opposite vertices), and these are concurrent
at the triangle's centroid
; indeed, they are the only area bisectors that go through the centroid. Three other area bisectors are parallel to the triangle's sides; each of these intersects the other two sides so as to divide them into segments with the proportions
. These six lines are concurrent three at a time: in addition to the three medians being concurrent, any one median is concurrent with two of the side-parallel area bisectors.
The envelope
of the infinitude of area bisectors is a deltoid
(broadly defined as a figure with three vertices connected by curves that are concave to the exterior of the deltoid, making the interior points a non-convex set). The vertices of the deltoid are at the midpoints of the medians; all points inside the deltoid are on three different area bisectors, while all points outside it are on just one. http://www.btinternet.com/~se16/js/halfarea.htm
The sides of the deltoid are arcs of hyperbola
s that are asymptotic
to the extended sides of the triangle.
Any line through a triangle that splits both the triangle's area and its perimeter in half goes through the triangle's incenter (the center of its incircle). There are either one, two, or three of these for any given triangle. A line through the incenter bisects one of the area or perimeter if and only if it also bisects the other.
bisects the area. Also, the diagonal
s of a parallelogram bisect each other.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, bisection is the division of something into two equal or congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
parts, usually by a line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
, which is then called a bisector. The most often considered types of bisectors are the segment bisector (a line that passes through the midpoint of a given segment) and the angle bisector (a line that passes through the apex of an angle, that divides it into two equal angles).
In three dimensional space, bisection is usually done by a plane, also called the bisector or bisecting plane.
Line segment bisector
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
bisector passes through the midpoint
Midpoint
The midpoint is the middle point of a line segment. It is equidistant from both endpoints.-Formulas:...
of the segment.
Particularly important is the perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
bisector of a segment, which, according to its name, meets the segment at right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
s. The perpendicular bisector of a segment also has the property that each of its points is equidistant
Equidistant
A point is said to be equidistant from a set of objects if the distances between that point and each object in the set are equal.In two-dimensional Euclidian geometry the locus of points equidistant from two given points is their perpendicular bisector...
from the segment's endpoints. Therefore Voronoi diagram
Voronoi diagram
In mathematics, a Voronoi diagram is a special kind of decomposition of a given space, e.g., a metric space, determined by distances to a specified family of objects in the space...
boundaries consist of segments of such lines or planes.
In classical geometry, the bisection is a simple compass and straightedge
Compass and straightedge
Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
, whose possibility depends on the ability to draw circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s of equal radii and different centers. The segment is bisected by drawing intersecting circles of equal radius, whose centers are the endpoints of the segment. The line determined by the points of intersection is the perpendicular bisector, and crosses our original segment at its center. This construction is in fact used when constructing a line perpendicular to a given line at a given point: drawing an arbitrary circle whose center is that point, it intersects the line in two more points, and the perpendicular to be constructed is the one bisecting the segment defined by these two points.
Angle bisector
An angleAngle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
bisector divides the angle into two angles with equal measures. An angle only has one bisector. Each point of an angle bisector is equidistant from the sides of the angle.
The interior bisector of an angle is the half-line or line segment that divides an angle of less than 180° into two equal angles. The exterior bisector is the half-line that divides the opposite angle (of greater than 180°) into two equal angles.
To bisect an angle with straightedge and compass, one draws a circle whose center is the vertex. The circle meets the angle at two points: one on each leg. Using each of these points as a center, draw two circles of the same size. The intersection of the circles (two points) determines a line that is the angle bisector.
The proof of the correctness of these two constructions is fairly intuitive, relying on the symmetry of the problem. It is interesting to note that the trisection of an angle (dividing it into three equal parts) cannot be achieved with the ruler and compass alone (this was first proved by Pierre Wantzel
Pierre Wantzel
Pierre Laurent Wantzel was a French mathematician who proved that several ancient geometric problems were impossible to solve using only compass and straightedge....
).
Angle bisectors of a triangle
The angle bisectors of the angles of a triangleTriangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
are concurrent in a point called the incenter of the triangle.
If the side lengths of a triangle are
, the semiperimeter () is , and A is the angle opposite side , the length of the internal bisector of angle A is.If the bisector of angle A in triangle ABC has length
and if this bisector divides the side opposite A into segments of lengths m and n, thenwhere b and c are the side lengths opposite vertices B and C; and the side opposite A is divided in the proportion b:c.
If the bisectors of angles A, B, and C have lengths
and , thenThe angle bisector theorem
Angle bisector theorem
In geometry, the angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.Consider a triangle...
is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle. It equates their relative lengths to the relative lengths of the other two sides of the triangle.
Area bisectors and area-perimeter bisectors of a triangle
There are an infinitude of lines that bisect the area of a triangleTriangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
. Three of them are the medians
Median (geometry)
In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposing side. Every triangle has exactly three medians; one running from each vertex to the opposite side...
of the triangle (which connect the sides' midpoints with the opposite vertices), and these are concurrent
Concurrent lines
In geometry, two or more lines are said to be concurrent if they intersect at a single point.In a triangle, four basic types of sets of concurrent lines are altitudes, angle bisectors, medians, and perpendicular bisectors:...
at the triangle's centroid
Centroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
; indeed, they are the only area bisectors that go through the centroid. Three other area bisectors are parallel to the triangle's sides; each of these intersects the other two sides so as to divide them into segments with the proportions
. These six lines are concurrent three at a time: in addition to the three medians being concurrent, any one median is concurrent with two of the side-parallel area bisectors.The envelope
Envelope (mathematics)
In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
of the infinitude of area bisectors is a deltoid
Deltoid curve
In geometry, a deltoid, also known as a tricuspoid or Steiner curve, is a hypocycloid of three cusps. In other words, it is the roulette created by a point on the circumference of a circle as it rolls without slipping along the inside of a circle with three times its radius...
(broadly defined as a figure with three vertices connected by curves that are concave to the exterior of the deltoid, making the interior points a non-convex set). The vertices of the deltoid are at the midpoints of the medians; all points inside the deltoid are on three different area bisectors, while all points outside it are on just one. http://www.btinternet.com/~se16/js/halfarea.htm
The sides of the deltoid are arcs of hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
s that are asymptotic
Asymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
to the extended sides of the triangle.
Any line through a triangle that splits both the triangle's area and its perimeter in half goes through the triangle's incenter (the center of its incircle). There are either one, two, or three of these for any given triangle. A line through the incenter bisects one of the area or perimeter if and only if it also bisects the other.
Area and diagonal bisectors of a parallelogram
Any line through the midpoint of a parallelogramParallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
bisects the area. Also, the diagonal
Diagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
s of a parallelogram bisect each other.
External links
- The Angle Bisector at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Angle Bisector definition. Math Open Reference With interactive applet
- Line Bisector definition. Math Open Reference With interactive applet
- Perpendicular Line Bisector. With interactive applet
- Animated instructions for bisecting an angle and bisecting a line Using a compass and straightedge