
Midpoint
Encyclopedia
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
of a line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
. It is equidistant
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
from both endpoints.
Formulas
The formulaFormula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
for determining the midpoint of a segment in the plane, with endpoints (x1) and (x2) is:

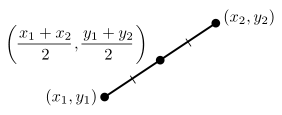
The formula for determining the midpoint of a segment in the plane, with endpoints (x1, y1) and (x2, y2) is:

The formula for determining the midpoint of a segment in the space, with endpoints (x1, y1, z1) and (x2, y2 z2) is:

More generally, for an n-dimensional space with axes
 , the midpoint of an interval is given by:
, the midpoint of an interval is given by:
Construction
The midpoint of a line segment can be located by first constructing a lens using circular arcs, then connecting the cusps of the lens. The point where the cusp-connecting line intersects the segment is then the midpoint. It is more challenging to locate the midpoint using only a compass, but it is still possible.Deriving the formula
In order to derive the formula you must understand the relationship between distance, and midpoint. Distance is very important in deriving the formula for midpoint. This is because the two are intertwined because when you have (x1, y1) and (x2,y2) there is a relationship in distance between these two points. This forms a line segment, but this isn't the relationship we are looking for. The relationship in distance that helps us derive the formula is Pythagorean Theorem. How this helps us is that there is a relationship that (x1, y1) and (x2,y2) with a third point. This Third point can be achieved by taking either x1 or x1 and y1 or y1. This third point allows us to make a triangle. which set of points you choose to use depends on which angle you are making the triangle at. Making a triangle helps us by because then we can use A2 + B2 = C2 to find the distance of the long side. The long side of the triangle would be the line segment that we are trying to find the midpoint of. After you use Pythagorean theorem you can find the midpoint of that by dividing it by 2, but that will not give you the coordinate point. This can be helpful because you can then apply the (x1,x2) and (y2,y1) to a A2 or B2. This would make the formula C2 = (y1 - y2)2 + (x1 - x2)2. This formula will not find midpoint, but it will assist someone in deriving the formula for midpoint from a formula that will find distance.See also
- Midpoint polygonMidpoint polygonIn geometry, the midpoint polygon of a polygon is the polygon whose vertices are the midpoints of the edges of .It is sometimes called the Kasner polygon after Edward Kasner, who termed it the inscribed polygon "for brevity"....
- Median (geometry)Median (geometry)In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposing side. Every triangle has exactly three medians; one running from each vertex to the opposite side...
- Segment bisectorBisectionIn geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector. The most often considered types of bisectors are the segment bisector and the angle bisector In geometry, bisection is the division of something into two equal...
- Numerical integration
External links
- Animation - showing the characteristics of the midpoint of a line segment

