
Triangular tiling
Encyclopedia
In geometry
, the triangular tiling is one of the three regular tiling
s of the Euclidean plane. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of {3,6}.
Conway
calls it a deltille, named from the triangular shape of the greek letter delta (Δ). The triangular tiling is roughly the kishextile.
It is one of three regular tilings of the plane. The other two are the square tiling and the hexagonal tiling.
This vertex arrangement
is called the A2 lattice.
s of a triangular tiling. (Naming the colors by indices on the 6 triangles around a vertex: 111111, 111112, 111212, 111213, 111222, 112122, 121212, 121213, 121314)
Four of the colorings are generated by Wythoff construction
s. Seven of the nine distinct colorings can be made as reductions of the four coloring: 121314. The remaining two, 111222 and 112122, have no Wythoff constructions.
. These can be expanded to Platonic solid
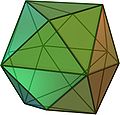
s: five, four and three triangles on a vertex define an icosahedron
, octahedron
, and tetrahedron
respectively.
This tiling is topologically related as a part of sequence of regular polyhedra with Schläfli symbols {3,n}, continuing into the hyperbolic plane
.
It is also topologically related as a part of sequence of Catalan solid
s with face configuration
Vn.6.6, and also continuing into the hyperbolic plane.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the triangular tiling is one of the three regular tiling
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
s of the Euclidean plane. Because the internal angle of the equilateral triangle is 60 degrees, six triangles at a point occupy a full 360 degrees. The triangular tiling has Schläfli symbol of {3,6}.
Conway
John Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
calls it a deltille, named from the triangular shape of the greek letter delta (Δ). The triangular tiling is roughly the kishextile.
It is one of three regular tilings of the plane. The other two are the square tiling and the hexagonal tiling.
This vertex arrangement
Vertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
is called the A2 lattice.
Uniform colorings
There are 9 distinct uniform coloringUniform coloring
In geometry, a uniform coloring is a property of a uniform figure that is colored to be vertex-transitive...
s of a triangular tiling. (Naming the colors by indices on the 6 triangles around a vertex: 111111, 111112, 111212, 111213, 111222, 112122, 121212, 121213, 121314)
Four of the colorings are generated by Wythoff construction
Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
s. Seven of the nine distinct colorings can be made as reductions of the four coloring: 121314. The remaining two, 111222 and 112122, have no Wythoff constructions.
| Coloring indices |
111111 | 121212 | 121314 | 121213 |
|---|---|---|---|---|
| Coloring |  |
 |
 |
|
| Symmetry | *632 (p6m) [6,3] |
*333 (p3m1) [3[3]] |
333 (p3) [3[3]]+ |
3*3 (p31m) [6,3+] |
| Wythoff symbol Wythoff symbol In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles.... |
6 | 3 2 | 3 | 3 3 | | 3 3 3 | |
| Coxeter-Dynkin Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
| Coloring indices |
111222 | 112122 | 111112 | 111212 | 111213 |
|---|---|---|---|---|---|
| Coloring |  |
 |
|||
| Symmetry | 2*22 (cmm) [∞,2+,∞] |
2222 (p2) [∞,2,∞]+ |
*333 (p3m1) [3[3]] |
*333 (p3m1) [3[3]] |
333 (p3) [3[3]]+ |
Related polyhedra and tilings
The planar tilings are related to polyhedra. Putting fewer triangles on a vertex leaves a gap and allows it to be folded into a pyramidPyramid
A pyramid is a structure whose outer surfaces are triangular and converge at a single point. The base of a pyramid can be trilateral, quadrilateral, or any polygon shape, meaning that a pyramid has at least three triangular surfaces...
. These can be expanded to Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s: five, four and three triangles on a vertex define an icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
, octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
, and tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
respectively.
This tiling is topologically related as a part of sequence of regular polyhedra with Schläfli symbols {3,n}, continuing into the hyperbolic plane
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
.
 {3,3} Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids... |
 {3,4} Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex.... |
 {3,5} Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... |
 {3,6} |
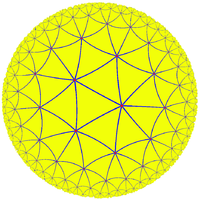 {3,7} |
 {3,8} |
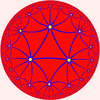 {3,9} |
It is also topologically related as a part of sequence of Catalan solid
Catalan solid
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean solid. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865....
s with face configuration
Face configuration
In geometry, a face configuration is notational description of a face-transitive polyhedron. It represents a sequential count of the number of faces that exist at each vertex around a face....
Vn.6.6, and also continuing into the hyperbolic plane.
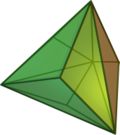 V3.6.6 Triakis tetrahedron In geometry, a triakis tetrahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated tetrahedron.It can be seen as a tetrahedron with triangular pyramids added to each face; that is, it is the Kleetope of the tetrahedron... |
 V4.6.6 Tetrakis hexahedron In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid. It can be seen as a cube with square pyramids covering each square face; that is, it is the Kleetope of the cube.... |
 V5.6.6 Pentakis dodecahedron In geometry, a pentakis dodecahedron is a Catalan solid. Its dual is the truncated icosahedron, an Archimedean solid.It can be seen as a dodecahedron with a pentagonal pyramid covering each face; that is, it is the Kleetope of the dodecahedron... |
 V6.6.6 |
 V7.6.6 Order-7 truncated triangular tiling In geometry, the Order 7 truncated heptagonal tiling, sometimes called the hyperbolic soccerball, is a semiregular tiling of the hyperbolic plane. There are two hexagons and one heptagon on each vertex, forming a pattern similar to a conventional soccer ball with heptagons in place of pentagons... |

