This article summarizes the classes of discrete

Discrete space

In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...

 planar symmetry groups

Symmetry group

The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...

. The symmetry groups are named here by three naming schemes: International notation, orbifold notation, and Coxeter's bracket notation.

There are three kinds of symmetry groups of the plane:

• 2 rosette groups – 2D point groups
• 7 frieze group
  Frieze group
  A frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
  
  s – 2D line groups
• 17 wallpaper group
  Wallpaper group
  A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
  
  s – 2D space group
  Space group
  In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
  
  s

Rosette groups

There are two families of discrete two-dimensional point groups, and they are specified with parameter n, which is the order of the group of the rotations in the group.

Family	Intl (orbifold Orbifold In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold... )	Geo	Schönflies Schoenflies notation The Schoenflies notation or Schönflies notation, named after the German mathematician Arthur Moritz Schoenflies, is one of two conventions commonly used to describe Point groups. This notation is used in spectroscopy. The other convention is the Hermann–Mauguin notation, also known as the...	Coxeter Coxeter notation In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M...	Order	Example
Cyclic symmetry	n (nn)		Cn	[n]+	n	5-fold rotation
Dihedral symmetry	nm (*nn)	n	Dn	[n]	2n	4-fold reflection

Frieze groups

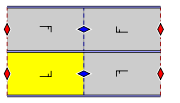
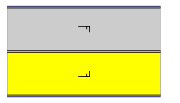
The 7 frieze group

Frieze group

A frieze group is a mathematical concept to classify designs on two-dimensional surfaces which are repetitive in one direction, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...

s, the two-dimensional line group

Line group

A line group is a mathematical way of describing symmetries associated with moving along a line. These symmetries include repeating along that line, making that line a one-dimensional lattice...

s, with a direction of periodicity are given with five notational names. The Schönflies notation is given as infinite limits of 7 dihedral groups. The yellow regions represent the infinite fundamental domain in each. Simple example images are given as periodic tilings on a cylinder with a periodicity of 6.

[∞,1], IUC (Orbifold) Geo Schönflies Schoenflies notation The Schoenflies notation or Schönflies notation, named after the German mathematician Arthur Moritz Schoenflies, is one of two conventions commonly used to describe Point groups. This notation is used in spectroscopy. The other convention is the Hermann–Mauguin notation, also known as the... Coxeter Coxeter notation In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M... Fundamental domain Example p1 (∞∞) p C∞ [∞,1]+ p1m1 (*∞∞) p1 C∞v [∞,1] [∞+,2], IUC (Orbifold) Geo Schönflies Coxeter Fundamental domain Example p11g (∞x) p.g1 S2∞ [∞+,2+] p11m (∞*) p.1 C∞h [∞+,2]

[∞,2], IUC (Orbifold) Geo Schönflies Coxeter Fundamental domain Example p2 (22∞) p D∞ [∞,2]+ p2mg (2*∞) p2g D∞d [∞,2+] p2mm (*22∞) p2 D∞h [∞,2]

Wallpaper groups

The 17 wallpaper group

Wallpaper group

A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...

s, with finite fundamental domains, are given by International notation

International notation

International notation may mean:*FDI World Dental Federation notation*Hermann-Mauguin notation - Crystallographic notation system*Decimal_mark#Influence_of_calculators_and_computers - the use of the decimal point as the decimal mark...

, orbifold notation, and Coxeter notation

Coxeter notation

In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M...

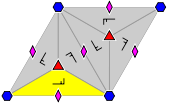
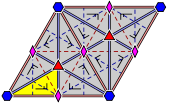
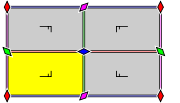
, classified by the 5 Bravais lattices in the plane: square

Square (geometry)

In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...

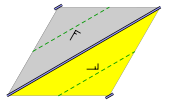
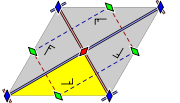
, oblique (parallelogrammatic), hexagonal (60 degree rhombic), rectangular, and centered rectangular (rhombic).

The p1 and p2 groups, with no reflectional symmetry, are repeated in all classes. The related pure reflectional Coxeter group

Coxeter group

In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...

 are given with all classes except oblique.

Square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... , [4,4], IUC (Orbifold) Geometric Coxeter Coxeter notation In geometry, Coxeter notation is a system of classifying symmetry groups, describing the angles between with fundamental reflections of a Coxeter group. It uses a bracketed notation, with modifiers to indicate certain subgroups. The notation is named after H. S. M... Fundamental domain p1 (o) p [∞+,2,∞+] p2 (2222) p [1+,4,4]+ p2gg pgg (22x) pg2g [4+,4+] p2mm pmm (*2222) p2 [1+,4,4] c2mm cmm (2*22) c2 4+,4+ p4 (442) p [4,4]+ p4gm p4g (4*2) pg4 [4+,4] p4mm p4m (*442) p4 [4,4] Parallelogram Parallelogram In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure... matic (oblique Oblique Oblique may refer to:*Oblique angle, in geometry, an angle that is not a multiple of 90 degrees*Oblique angle, synonym for Dutch angle, a cinematographic technique*Oblique , by jazz vibraphonist Bobby Hutcherson... ) p1 (o) p [∞+,2,∞+] p2 (2222) p [∞,2,∞]+

Hexagonal [6,3], IUC (Orbifold) Coxeter Fundamental domain p1 (o) p [∞+,2,∞+] p2 (2222) p [∞,2,∞]+ p3 (333) p [1+,6,3+] p3m1 (*333) p3 [1+,6,3] p31m (3*3) h3 [6,3+] c2mm cmm (2*22) c2 [∞,2+,∞] p6 (632) p [6,3]+ p6mm p6m (*632) p6 [6,3] Hexagonal [3[3]], p3 (333) p [3[3]]+ p3m1 (*333) p3 [3[3]] p31m (3*3) h3 [3[3[3]]+] p6 (632) p [3[3[3]]]+ p6mm p6m (*632) p6 [3[3[3]]]

Rectangular Rectangle In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle... , [∞h,2,∞v], IUC (Orbifold) Coxeter Fundamental domain p1 (o) p [∞+,2,∞+] p2 (2222) p [∞,2,∞]+ p11g pg(h) (xx) pg1 h: [∞+,(2,∞)+] p1g1 pg(v) (xx) pg1 v: [(∞,2)+,∞+] p2gm pgm (22*) pg2 h: [(∞,2)+,∞] p2mg pmg (22*) pg2 v: [∞,(2,∞)+] p11m pm(h) (**) p1 h: [∞+,2,∞] p1m1 pm(v) (**) p1 v: [∞,2,∞+] p2mm pmm (*2222) p2 [∞,2,∞] Rhombic Rhombus In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every... , [∞h,2+,∞v], p1 (o) p [∞+,2,∞+] p2 (2222) p [∞,2,∞]+ c11m cm(h) (*x) c1 h: [∞+,2+,∞] c1m1 cm(v) (*x) c1 v: [∞,2+,∞+] p2gg pgg (22x) pg2g [∞+,2+,∞+] c2mm cmm (2*22) c2 [∞,2+,∞]

External links

• "Conway's manuscript" on Orbifold notation (Notation changed from this original, x is now used in place of open-dot, and o is used in place of the closed dot)
• The 17 Wallpaper Groups