
Discrete space
Encyclopedia
In topology
, a discrete space is a particularly simple example of a topological space
or similar structure, one in which the points are "isolated
" from each other in a certain sense.
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, a discrete space is a particularly simple example of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
or similar structure, one in which the points are "isolated
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
" from each other in a certain sense.
Definitions
Given a set X:- the discrete topology on X is defined by letting every subsetSubsetIn mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of X be openOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
(and hence also closedClosed setIn geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
), and X is a discrete topological space if it is equipped with its discrete topology; - the discrete uniformityUniform spaceIn the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
on X is defined by letting every supersetSuperSetSuperSet Software was a group founded by friends and former Eyring Research Institute co-workers Drew Major, Dale Neibaur, Kyle Powell and later joined by Mark Hurst...
of the diagonal {(x,x) : x is in X} in X × X be an entourage, and X is a discrete uniform space if it is equipped with its discrete uniformity. - the discrete metricMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
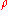 on X is defined by
on X is defined by
for any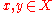 . In this case
. In this case 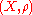 is called a discrete metric space or a space of isolated pointIsolated pointIn topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
is called a discrete metric space or a space of isolated pointIsolated pointIn topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
s.- a set S is discrete in a metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
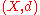 , for
, for  , if for every
, if for every 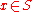 , there exists some
, there exists some  (depending on
(depending on  ) such that
) such that 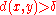 for all
for all  ; such a set consists of isolated pointIsolated pointIn topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
; such a set consists of isolated pointIsolated pointIn topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
s. A set S is uniformly discrete in the metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
 , for
, for  , if there exists ε > 0 such that for any two distinct
, if there exists ε > 0 such that for any two distinct 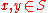 ,
, 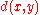 > ε.
> ε.
A metric space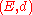 is said to be uniformly discrete if there exists
is said to be uniformly discrete if there exists  such that, for any
such that, for any 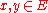 , one has either
, one has either  or
or 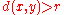 . The topology underlying a metric space can be discrete, without the metric being uniformly discrete: for example the usual metric on the set {1, 1/2, 1/4, 1/8, ...} of real numbers.
. The topology underlying a metric space can be discrete, without the metric being uniformly discrete: for example the usual metric on the set {1, 1/2, 1/4, 1/8, ...} of real numbers.
Properties
The underlying uniformity on a discrete metric space is the discrete uniformity, and the underlying topology on a discrete uniform space is the discrete topology.
Thus, the different notions of discrete space are compatible with one another.
On the other hand, the underlying topology of a non-discrete uniform or metric space can be discrete; an example is the metric space X := {1/n : n = 1,2,3,...} (with metric inherited from the real lineReal lineIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
and given by d(x,y) = |x − y|).
Obviously, this is not the discrete metric; also, this space is not complete and hence not discrete as a uniform space.
Nevertheless, it is discrete as a topological space.
We say that X is topologically discrete but not uniformly discrete or metrically discrete.
Additionally:- The topological dimension of a discrete space is equal to 0.
- A topological space is discrete if and only if its singletons are open, which is the case if and only if it doesn't contain any accumulation points.
- The singletons form a basis for the discrete topology.
- A uniform space X is discrete if and only if the diagonal {(x,x) : x is in X} is an entourage.
- Every discrete topological space satisfies each of the separation axioms; in particular, every discrete space is HausdorffHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, that is, separated. - A discrete space is compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is finite. - Every discrete uniform or metric space is completeComplete spaceIn mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
. - Combining the above two facts, every discrete uniform or metric space is totally boundedTotally bounded spaceIn topology and related branches of mathematics, a totally bounded space is a space that can be covered by finitely many subsets of any fixed "size" . The smaller the size fixed, the more subsets may be needed, but any specific size should require only finitely many subsets...
if and only if it is finite. - Every discrete metric space is bounded.
- Every discrete space is first-countableFirst-countable spaceIn topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis...
; it is moreover second-countableSecond-countable spaceIn topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
if and only if it is countable. - Every discrete space with at least two points is totally disconnected.
- Every non-empty discrete space is second category.
- Any two discrete spaces with the same cardinality are homeomorphic.
- Every discrete space is metrizable (by the discrete metric).
- A finite space is metrizable only if it is discrete.
- If X is a topological space and Y is a set carrying the discrete topology, then X is evenly covered by (the projection map is the desired covering)
- The subspace topologySubspace topologyIn topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
on the integers as a subspace of the real lineReal lineIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
is the discrete topology.
Any function from a discrete topological space to another topological space is continuous, and any function from a discrete uniform space to another uniform space is uniformly continuous. That is, the discrete space X is freeFree objectIn mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
on the set X in the categoryCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
of topological spaces and continuous maps or in the category of uniform spaces and uniformly continuous maps. These facts are examples of a much broader phenomenon, in which discrete structures are usually free on sets.
With metric spaces, things are more complicated, because there are several categories of metric spaces, depending on what is chosen for the morphismMorphismIn mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s. Certainly the discrete metric space is free when the morphisms are all uniformly continuous maps or all continuous maps, but this says nothing interesting about the metric structureMathematical structureIn mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....
, only the uniform or topological structure. Categories more relevant to the metric structure can be found by limiting the morphisms to Lipschitz continuous maps or to short mapShort mapIn the mathematical theory of metric spaces, a metric map is a function between metric spaces that does not increase any distance .These maps are the morphisms in the category of metric spaces, Met ....
s; however, these categories don't have free objects (on more than one element). However, the discrete metric space is free in the category of bounded metric spaces and Lipschitz continuous maps, and it is free in the category of metric spaces bounded by 1 and short maps. That is, any function from a discrete metric space to another bounded metric space is Lipschitz continuous, and any function from a discrete metric space to another metric space bounded by 1 is short.
Going the other direction, a function f from a topological space Y to a discrete space X is continuous if and only it if is locally constantLocally constant functionIn mathematics, a function f from a topological space A to a set B is called locally constant, if for every a in A there exists a neighborhood U of a, such that f is constant on U....
in the sense that every point in Y has a neighborhood on which f is constant.
Uses
A discrete structure is often used as the "default structure" on a set that doesn't carry any other natural topology, uniformity, or metric; discrete structures can often be used as "extreme" examples to test particular suppositions. For example, any groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
can be considered as a topological groupTopological groupIn mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
by giving it the discrete topology, implying that theorems about topological groups apply to all groups. Indeed, analysts may refer to the ordinary, non-topological groups studied by algebraists as "discrete groupDiscrete groupIn mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
s" . In some cases, this can be usefully applied, for example in combination with Pontryagin dualityPontryagin dualityIn mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
. A 0-dimensional manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
(or differentiable or analytical manifold) is nothing but a discrete topological space. We can therefore view any discrete group as a 0-dimensional Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
.
A productProduct topologyIn topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
of countably infinitely many copies of the discrete space of natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s is homeomorphic to the space of irrational numberIrrational numberIn mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s, with the homeomorphism given by the continued fractionContinued fractionIn mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
expansion. A product of countably infinitely many copies of the discrete space {0,1} is homeomorphic to the Cantor setCantor setIn mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
; and in fact uniformly homeomorphic to the Cantor set if we use the product uniformity on the product. Such a homeomorphism is given by ternary notation of numbers. (See Cantor spaceCantor spaceIn mathematics, a Cantor space, named for Georg Cantor, is a topological abstraction of the classical Cantor set: a topological space is a Cantor space if it is homeomorphic to the Cantor set. In set theory, the topological space 2ω is called "the" Cantor space...
.)
In the foundations of mathematicsFoundations of mathematicsFoundations of mathematics is a term sometimes used for certain fields of mathematics, such as mathematical logic, axiomatic set theory, proof theory, model theory, type theory and recursion theory...
, the study of compactnessCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
properties of products of {0,1} is central to the topological approach to the ultrafilter principleBoolean prime ideal theoremIn mathematics, a prime ideal theorem guarantees the existence of certain types of subsets in a given abstract algebra. A common example is the Boolean prime ideal theorem, which states that ideals in a Boolean algebra can be extended to prime ideals. A variation of this statement for filters on...
, which is a weak form of choice.
Indiscrete spaces
In some ways, the opposite of the discrete topology is the trivial topologyTrivial topologyIn topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such a space is sometimes called an indiscrete space, and its topology sometimes called an indiscrete topology...
(also called the indiscrete topology), which has the fewest possible open sets (just the empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
and the space itself). Where the discrete topology is initial or free, the indiscrete topology is final or cofree: every function from a topological space to an indiscrete space is continuous, etc.
Quotation
- Stanislaw Ulam characterized Los AngelesLos Angeles, CaliforniaLos Angeles , with a population at the 2010 United States Census of 3,792,621, is the most populous city in California, USA and the second most populous in the United States, after New York City. It has an area of , and is located in Southern California...
as "a discrete space, in which there is an hour's drive between points".
- a set S is discrete in a metric space

