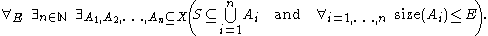Totally bounded space
Encyclopedia
In topology
and related branches of mathematics
, a totally bounded space is a space that can be cover
ed by finitely many subset
s of any fixed "size" (where the meaning of "size" depends on the given context). The smaller the size fixed, the more subsets may be needed, but any specific size should require only finitely many subsets. A related notion is a totally bounded set, in which only a subset of the space needs to be covered. Every subset of a totally bounded space is a totally bounded set; but even if a space is not totally bounded, some of its subsets still will be.
The term precompact (or pre-compact) is sometimes used with the same meaning, but `pre-compact' is also used to mean relatively compact. In a complete metric space
these meanings coincide but in general they do not. See also use of the axiom of choice below.
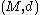is totally bounded
if and only if for every real number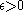
, there exists
a finite collection of open balls in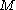
of radius 
whose union
contains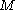
. Equivalently, the metric space 
is totally bounded if and only if
for every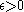
, there exists a finite cover such that the radius of each
element of the cover is at most
. This is equivalent to the existence of a finite ε-net
.
Each totally bounded space is bounded
(as the union of finitely many bounded sets is bounded), but the converse is not true in general.
For example, an infinite set equipped with a discrete metric is bounded but not totally bounded.
If M is Euclidean space
and d is the Euclidean distance
, then
a subset (with the subspace topology
) is totally bounded if and only if it is bounded.
is: A subset S of a space X is a totally bounded set if and only if, given any size E, there exist a natural number
n and a family
A1, A2, ..., An of subsets of X, such that S is contained in the union
of the family (in other words, the family is a finite cover of S), and such that each set Ai in the family is of size E (or less). In mathematical symbols:
The space X is a totally bounded space if and only if it is a totally bounded set when considered as a subset of itself.
(One can also define totally bounded spaces directly, and then define a set to be totally bounded if and only if it is totally bounded when considered as a subspace.)
The terms "space" and "size" here are vague, and they may be made precise in various ways:
A subset S of a metric space
X is totally bounded if and only if, given any positive real number
E, there exists a finite cover of S by subsets of X whose diameter
s are all less than E. (In other words, a "size" here is a positive real number, and a subset is of size E if its diameter is less than E.) Equivalently, S is totally bounded if and only if, given any E as before, there exist elements a1, a2, ..., an of X such that S is contained in the union of the n open balls of radius E around the points ai.
A subset S of a topological vector space
, or more generally topological abelian group
, X is totally bounded if and only if, given any neighbourhood E of the identity (zero) element
of X, there exists a finite cover of S by subsets of X each of which is a translate of a subset of E. (In other words, a "size" here is a neighbourhood of the identity element, and a subset is of size E if it is translate of a subset of E.) Equivalently, S is totally bounded if and only if, given any E as before, there exist elements a1, a2, ..., an of X such that S is contained in the union of the n translates of E by the points ai.
A topological group
X is left-totally bounded if and only if it satisfies the definition for topological abelian groups above, using left translates. That is, use aiE in place of E + ai. Alternatively, X is right-totally bounded if and only if it satisfies the definition for topological abelian groups above, using right translates. That is, use Eai in place of E + ai. (In other words, a "size" here is unambiguously a neighbourhood of the identity element, but there are two notions of whether a set is of a given size: a left notion based on left translation and a right notion based on right translation.)
Generalising the above definitions, a subset S of a uniform space
X is totally bounded if and only if, given any entourage E in X, there exists a finite cover of S by subsets of X each of whose Cartesian squares is a subset of E. (In other words, a "size" here is an entourage, and a subset is of size E if its Cartesian square is a subset of E.) Equivalently, S is totally bounded if and only if, given any E as before, there exist subsets A1, A2, ..., An of X such that S is contained in the union of the Ai and, whenever the elements x and y of X both belong to the same set Ai, then (x,y) belongs to E (so that x and y are close as measured by E).
The definition can be extended still further, to any category of spaces with a notion of compactness and Cauchy completion: a space is totally bounded if and only if its completion is compact.
Every compact metric space is totally bounded.
A uniform space is compact if and only if
it is both totally bounded and Cauchy complete. This can be seen as a generalisation of the Heine-Borel theorem from Euclidean space
s to arbitrary spaces: we must replace boundedness
with total boundedness (and also replace closedness
with completeness).
There is a complementary relationship between total boundedness and the process of Cauchy completion: A uniform space is totally bounded if and only if its Cauchy completion is totally bounded. (This corresponds to the fact that, in Euclidean spaces, a set is bounded if and only if its closure is bounded.)
Combining these theorems, a uniform space is totally bounded if and only if its completion is compact. This may be taken as an alternative definition of total boundedness. Alternatively, this may be taken as a definition of precompactness, while still using a separate definition of total boundedness. Then it becomes a theorem that a space is totally bounded if and only if it is precompact. (Separating the definitions in this way is useful in the absence of the axiom of choice; see the next section.)
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
and related branches of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a totally bounded space is a space that can be cover
Cover (topology)
In mathematics, a cover of a set X is a collection of sets whose union contains X as a subset. Formally, ifC = \lbrace U_\alpha: \alpha \in A\rbrace...
ed by finitely many subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of any fixed "size" (where the meaning of "size" depends on the given context). The smaller the size fixed, the more subsets may be needed, but any specific size should require only finitely many subsets. A related notion is a totally bounded set, in which only a subset of the space needs to be covered. Every subset of a totally bounded space is a totally bounded set; but even if a space is not totally bounded, some of its subsets still will be.
The term precompact (or pre-compact) is sometimes used with the same meaning, but `pre-compact' is also used to mean relatively compact. In a complete metric space
these meanings coincide but in general they do not. See also use of the axiom of choice below.
Definition for a metric space
A metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
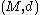is totally boundedif and only if for every real number
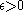, there existsa finite collection of open balls in
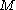of radius whose unioncontains
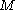. Equivalently, the metric space is totally bounded if and only iffor every
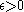, there exists a finite cover such that the radius of eachelement of the cover is at most
. This is equivalent to the existence of a finite ε-netΕ-net (metric spaces)
In the mathematics of metric spaces, an \varepsilon-net, or epsilon net relates to having a set which approximates another in the sense that any point in the second set is within a small distance of a point in the first set....
.
Each totally bounded space is bounded
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
(as the union of finitely many bounded sets is bounded), but the converse is not true in general.
For example, an infinite set equipped with a discrete metric is bounded but not totally bounded.
If M is Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
and d is the Euclidean distance
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
, then
a subset (with the subspace topology
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
) is totally bounded if and only if it is bounded.
Definitions in other contexts
The general logical form of the definitionDefinition
A definition is a passage that explains the meaning of a term , or a type of thing. The term to be defined is the definiendum. A term may have many different senses or meanings...
is: A subset S of a space X is a totally bounded set if and only if, given any size E, there exist a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n and a family
Family of sets
In set theory and related branches of mathematics, a collection F of subsets of a given set S is called a family of subsets of S, or a family of sets over S. More generally, a collection of any sets whatsoever is called a family of sets...
A1, A2, ..., An of subsets of X, such that S is contained in the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of the family (in other words, the family is a finite cover of S), and such that each set Ai in the family is of size E (or less). In mathematical symbols:
The space X is a totally bounded space if and only if it is a totally bounded set when considered as a subset of itself.
(One can also define totally bounded spaces directly, and then define a set to be totally bounded if and only if it is totally bounded when considered as a subspace.)
The terms "space" and "size" here are vague, and they may be made precise in various ways:
A subset S of a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
X is totally bounded if and only if, given any positive real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
E, there exists a finite cover of S by subsets of X whose diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
s are all less than E. (In other words, a "size" here is a positive real number, and a subset is of size E if its diameter is less than E.) Equivalently, S is totally bounded if and only if, given any E as before, there exist elements a1, a2, ..., an of X such that S is contained in the union of the n open balls of radius E around the points ai.
A subset S of a topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
, or more generally topological abelian group
Topological abelian group
In mathematics, a topological abelian group, or TAG, is a topological group that is also an abelian group.That is, a TAG is both a group and a topological space, the group operations are continuous, and the group's binary operation is commutative....
, X is totally bounded if and only if, given any neighbourhood E of the identity (zero) element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of X, there exists a finite cover of S by subsets of X each of which is a translate of a subset of E. (In other words, a "size" here is a neighbourhood of the identity element, and a subset is of size E if it is translate of a subset of E.) Equivalently, S is totally bounded if and only if, given any E as before, there exist elements a1, a2, ..., an of X such that S is contained in the union of the n translates of E by the points ai.
A topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
X is left-totally bounded if and only if it satisfies the definition for topological abelian groups above, using left translates. That is, use aiE in place of E + ai. Alternatively, X is right-totally bounded if and only if it satisfies the definition for topological abelian groups above, using right translates. That is, use Eai in place of E + ai. (In other words, a "size" here is unambiguously a neighbourhood of the identity element, but there are two notions of whether a set is of a given size: a left notion based on left translation and a right notion based on right translation.)
Generalising the above definitions, a subset S of a uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
X is totally bounded if and only if, given any entourage E in X, there exists a finite cover of S by subsets of X each of whose Cartesian squares is a subset of E. (In other words, a "size" here is an entourage, and a subset is of size E if its Cartesian square is a subset of E.) Equivalently, S is totally bounded if and only if, given any E as before, there exist subsets A1, A2, ..., An of X such that S is contained in the union of the Ai and, whenever the elements x and y of X both belong to the same set Ai, then (x,y) belongs to E (so that x and y are close as measured by E).
The definition can be extended still further, to any category of spaces with a notion of compactness and Cauchy completion: a space is totally bounded if and only if its completion is compact.
Examples and nonexamples
- A subset of the real lineReal lineIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, or more generally of (finite-dimensional) Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, is totally bounded if and only if it is boundedBounded setIn mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
. Archimedean property is used. - The unit ball in a Hilbert spaceHilbert spaceThe mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, or more generally in a Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, is totally bounded if and only if the space has finite dimension. - Every compact set is totally bounded, whenever the concept is defined.
- Every totally bounded metric space is bounded. However not every bounded metric space is totally bounded.
- A subset of a complete metric space is totally bounded if and only if it is relatively compact (meaning that its closureClosure (topology)In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
is compact). - In a locally convex space endowed with the weak topologyWeak topology (polar topology)In functional analysis and related areas of mathematics the weak topology is the coarsest polar topology, the topology with the fewest open sets, on a dual pair...
the precompact sets are exactly the bounded setBounded set (topological vector space)In functional analysis and related areas of mathematics, a set in a topological vector space is called bounded or von Neumann bounded, if every neighborhood of the zero vector can be inflated to include the set...
s. - A metric space is separable if and only if it is homeomorphicHomeomorphismIn the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
to a totally bounded metric space. - An infinite metric space with the discrete metric (the distance between any two distinct points is 1) is not totally bounded, even though it is bounded.
Relationships with compactness and completeness
There is a nice relationship between total boundedness and compactness:Every compact metric space is totally bounded.
A uniform space is compact if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
it is both totally bounded and Cauchy complete. This can be seen as a generalisation of the Heine-Borel theorem from Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s to arbitrary spaces: we must replace boundedness
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
with total boundedness (and also replace closedness
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
with completeness).
There is a complementary relationship between total boundedness and the process of Cauchy completion: A uniform space is totally bounded if and only if its Cauchy completion is totally bounded. (This corresponds to the fact that, in Euclidean spaces, a set is bounded if and only if its closure is bounded.)
Combining these theorems, a uniform space is totally bounded if and only if its completion is compact. This may be taken as an alternative definition of total boundedness. Alternatively, this may be taken as a definition of precompactness, while still using a separate definition of total boundedness. Then it becomes a theorem that a space is totally bounded if and only if it is precompact. (Separating the definitions in this way is useful in the absence of the axiom of choice; see the next section.)