
Euclidean distance
Encyclopedia
In mathematics
, the Euclidean distance or Euclidean metric is the "ordinary" distance
between two points that one would measure with a ruler, and is given by the Pythagorean formula
. By using this formula as distance, Euclidean space (or even any inner product space
) becomes a metric space
. The associated norm
is called the Euclidean norm. Older literature refers to the metric as Pythagorean metric.
connecting them ( ).
).
In Cartesian coordinates, if p = (p1, p2,..., pn) and q = (q1, q2,..., qn) are two points in Euclidean n-space
, then the distance from p to q, or from q to p is given by:
The position of a point in a Euclidean n-space is a Euclidean vector. So, p and q are Euclidean vectors, starting from the origin of the space, and their tips indicate two points. The Euclidean norm, or Euclidean length, or magnitude of a vector measures the length of the vector:
where the last equation involves the dot product
.
A vector can be described as a directed line segment from the origin
of the Euclidean space (vector tail), to a point in that space (vector tip). If we consider that its length is actually the distance from its tail to its tip, it becomes clear that the Euclidean norm of a vector is just a special case of Euclidean distance: the Euclidean distance between its tail and its tip.
The distance between points p and q may have a direction (e.g. from p to q), so it may be represented by another vector, given by

In a three-dimensional space (n=3), this is an arrow from p to q, which can be also regarded as the position of q relative to p. It may be also called a displacement
vector if p and q represent two positions of the same point at two successive instants of time.
The Euclidean distance between p and q is just the Euclidean length of this distance (or displacement) vector:
which is equivalent to equation 1, and also to:

is the absolute value
of their numerical difference. Thus if x and y are two points on the real line, then the distance between them is given by: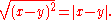
In one dimension, there is a single homogeneous, translation-invariant metric
(in other words, a distance that is induced by a norm
), up to a scale factor of length, which is the Euclidean distance. In higher dimensions there are other possible norms.

Alternatively, it follows from that if the polar coordinates of the point p are (r1, θ1) and those of q are (r2, θ2), then the distance between the points is

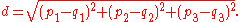

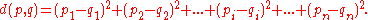
Squared Euclidean Distance is not a metric as it does not satisfy the triangle inequality
, however it is frequently used in optimization problems in which distances only have to be compared.
It is also referred to as quadrance within the field of rational trigonometry
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Euclidean distance or Euclidean metric is the "ordinary" distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
between two points that one would measure with a ruler, and is given by the Pythagorean formula
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
. By using this formula as distance, Euclidean space (or even any inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
) becomes a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. The associated norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
is called the Euclidean norm. Older literature refers to the metric as Pythagorean metric.
Definition
The Euclidean distance between points p and q is the length of the line segmentLine segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
connecting them (
 ).
).In Cartesian coordinates, if p = (p1, p2,..., pn) and q = (q1, q2,..., qn) are two points in Euclidean n-space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, then the distance from p to q, or from q to p is given by:
The position of a point in a Euclidean n-space is a Euclidean vector. So, p and q are Euclidean vectors, starting from the origin of the space, and their tips indicate two points. The Euclidean norm, or Euclidean length, or magnitude of a vector measures the length of the vector:

where the last equation involves the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
.
A vector can be described as a directed line segment from the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
of the Euclidean space (vector tail), to a point in that space (vector tip). If we consider that its length is actually the distance from its tail to its tip, it becomes clear that the Euclidean norm of a vector is just a special case of Euclidean distance: the Euclidean distance between its tail and its tip.
The distance between points p and q may have a direction (e.g. from p to q), so it may be represented by another vector, given by

In a three-dimensional space (n=3), this is an arrow from p to q, which can be also regarded as the position of q relative to p. It may be also called a displacement
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
vector if p and q represent two positions of the same point at two successive instants of time.
The Euclidean distance between p and q is just the Euclidean length of this distance (or displacement) vector:
which is equivalent to equation 1, and also to:

One dimension
In one dimension, the distance between two points on the real lineReal line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
is the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of their numerical difference. Thus if x and y are two points on the real line, then the distance between them is given by:
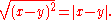
In one dimension, there is a single homogeneous, translation-invariant metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
(in other words, a distance that is induced by a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
), up to a scale factor of length, which is the Euclidean distance. In higher dimensions there are other possible norms.
Two dimensions
In the Euclidean plane, if p = (p1, p2) and q = (q1, q2) then the distance is given by
Alternatively, it follows from that if the polar coordinates of the point p are (r1, θ1) and those of q are (r2, θ2), then the distance between the points is

Three dimensions
In three-dimensional Euclidean space, the distance is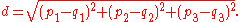
N dimensions
In general, for an n-dimensional space, the distance is
Squared Euclidean Distance
The standard Euclidean distance can be squared in order to place progressively greater weight on objects that are further apart. In this case, the equation becomes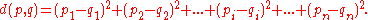
Squared Euclidean Distance is not a metric as it does not satisfy the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
, however it is frequently used in optimization problems in which distances only have to be compared.
It is also referred to as quadrance within the field of rational trigonometry
Rational trigonometry
Rational trigonometry is a recently introduced approach to trigonometry that eschews all transcendental functions and all proportional measurements of angles. In place of angles, it characterizes the separation between lines by a quantity called the "spread", which is a rational function of their...
.
See also
- Mahalanobis distanceMahalanobis distanceIn statistics, Mahalanobis distance is a distance measure introduced by P. C. Mahalanobis in 1936. It is based on correlations between variables by which different patterns can be identified and analyzed. It gauges similarity of an unknown sample set to a known one. It differs from Euclidean...
normalizes based on a covariance matrix to make the distance metric scale-invariant. - Manhattan distance measures distance following only axis-aligned directions.
- Chebyshev distanceChebyshev distanceIn mathematics, Chebyshev distance , Maximum metric, or L∞ metric is a metric defined on a vector space where the distance between two vectors is the greatest of their differences along any coordinate dimension...
measures distance assuming only the most significant dimension is relevant. - Minkowski distanceMinkowski distanceThe Minkowski distance is a metric on Euclidean space which can be considered as a generalization of both the Euclidean distance and the Manhattan distance.-Definition:The Minkowski distance of order p between two pointsis defined as:...
is a generalization that unifies Euclidean distance, Manhattan distance, and Chebyshev distance. - MetricMetric (mathematics)In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
- Pythagorean addition

